Pole-Zero Plot

POLE –ZERO PLOT

1.     X(z) is a rational function, that is a ratio of two polynomials in z^-1 or z.

The roots of the denominator or the value of z for which X(z) becomes infinite, defines locations of the poles. The roots of the numerator or the value of z for which X(z) becomes zero, defines locations of the zeros.

2.     ROC dos not contain any poles of X(z). This is because x(z) becomes infinite at the locations of the poles. Only poles affect the causality and stability of the system.

3.     CASUALTY CRITERIA FOR LSI SYSTEM

LSI system is causal if and only if the ROC the system function is exterior to the circle. i. e |z| > r. This is the condition for causality of the LSI system in terms of z transform.

(The condition for LSI system to be causal is h(n) = 0 ….. n<0 )

4.     STABILITY CRITERIA FOR LSI SYSTEM

Bounded input x(n) produces bounded output y(n) in the LSI system only if

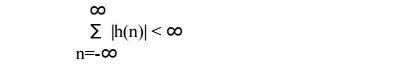
With this condition satisfied, the system will be stable. The above equation states that the LSI system is stable if its unit sample response is absolutely summable. This is necessary and sufficient condition for the stability of LSI system.

Taking magnitude of both the sides

Magnitudes of overall sum is less than the sum of magnitudes of individual sums.

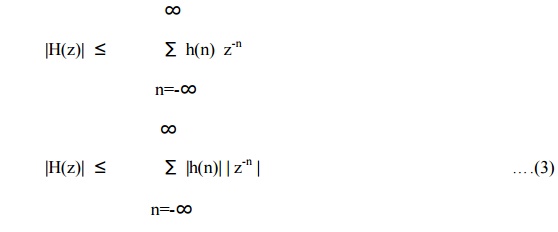
5.     If H(z) is evaluated on the unit circle | z^-n|=|z|=1.

Hence LSI system is stable if and only if the ROC the system function includes the unit circle. i.e r < 1. This is the condition for stability of the LSI system in terms of z transform. Thus

For stable system |z| < 1

For unstable system |z| > 1

Marginally stable system |z| = 1

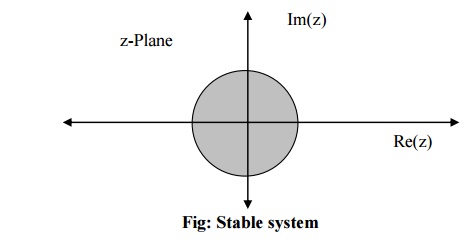
Poles inside unit circle gives stable system.Poles outside unit circle gives unstable system. Poles on unit circle give marginally stable system.

6.     A causal and stable system must have a system function that converges for |z| > r < 1.

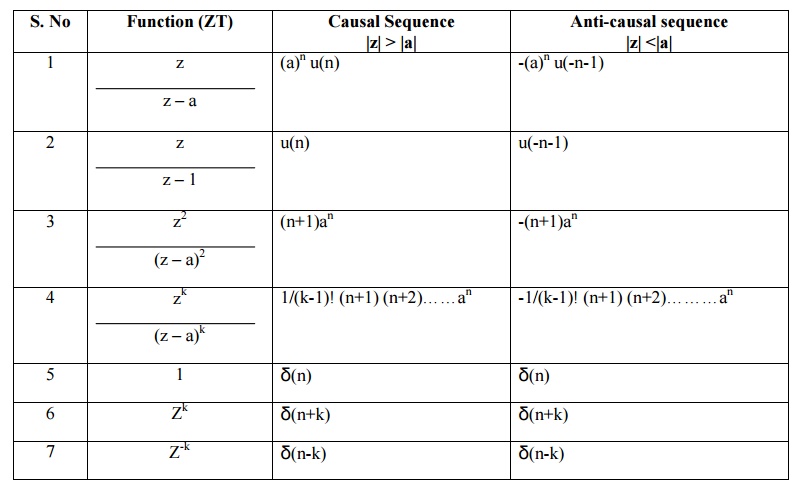
STANDARD INVERSE Z TRANSORMS