Inverse Z Transform (IZT)

INVERSE Z TRANSFORM (IZT)

The signal can be converted from time domain into z domain with the help of z transform (ZT). Similar way the signal can be converted from z domain to time domain with the help of inverse z transform(IZT). The inverse z transform can be obtained by using two different methods.

1)    Partial fraction expansion Method (PFE) / Application of residue theorem

2)    Power series expansion Method (PSE)

1.    PARTIAL FRACTION EXPANSION METHOD

In this method X(z) is first expanded into sum of simple partial fraction

The above equation can be written in partial fraction expansion form and find the coefficient A_K and take IZT.

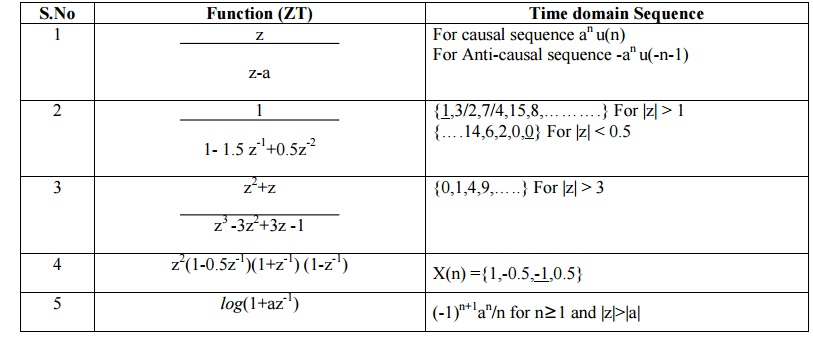
SOLVE USING PARTIAL FRACTION EXPANSION METHOD (PFE)

2.    RESIDUE THEOREM METHOD

In this method, first find G(z)= z^n-1 X(Z) and find the residue of G(z) at various poles of X(z).

3.  POWER-SERIES EXPANSION METHOD

The z transform of a discrete time signal x(n) is given as

Expanding the above terms we have

x(z) = …..+x(-2)Z²+ x(-1)Z+ x(0)+ x(1) Z^-1 + x(2) Z² +….. (2) 

This is the expansion of z transform in power series form. Thus sequence x(n) is given as

 x(n) ={ ….. ,x(-2),x(-1),x(0),x(1),x(2),…………..}.

Power series can be obtained directly or by long division method.

SOLVE USING “POWER SERIES EXPANSION” METHOD

RECURSIVE ALGORITHM

The long division method can be recast in recursive form.