Chapter: Mechanical : Gas Dynamics and Jet Propulsion : Flow Through Ducts
Rayleigh line (or) curve
Rayleigh line (or) curve
The friction less flow of a perfect gas through a constant
area duct in which heat transfer to or from the gas is the dominant factor
bringing about changes in the flow is referred to as Rayleigh flow or diabetic
flow. In thermodynamic coordinates, the Rayleigh flow process can be described
by a curve known as Rayleigh line and is defined as the locus of quasi- static
thermodynamic state points traced during the flow. The Rayleigh line satisfies
the equation of state along with simple forms of continuity and momentum
equation.
Governing Equations
In order to formulate the equation for the Rayleigh line,
let us consider steady flow of a perfect gas through a constant area passage in
which transfer of heat with the surroundings is the major factor responsible
for changes in fluid properties. The simple form of continuity equation for
steady one dimensional flow in a constant area duct is
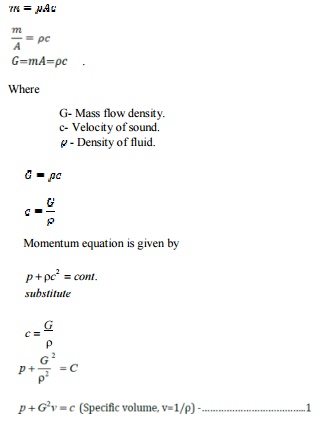
Where
G- Mass flow density.
c- Velocity of sound.
p- Density of fluid.
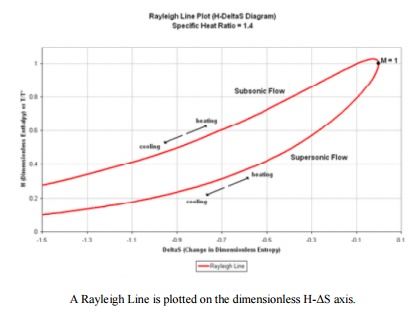
Equation 1 may be used for representing Rayleigh line on
the h- s diagram, as illustrated in fig shown in below. In general, most of the
fluids in practical use have Rayleigh curves of the general form shown in fig.
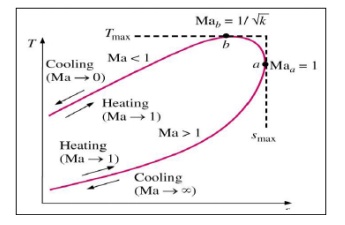
The portion of the Rayleigh curve above the point of
maximum entropy usually represents subsonic flow (M<1) and the portion below
the maximum entropy point represents supersonic flow (M>1).
An entropy increases due to heat addition and entropy
decreases due to heat rejection. Therefore, the Mach number is increased by
heating and decreased by cooling at subsonic speeds. On the other hand, the
Mach number is decreased by heating and increased by cooling at supersonic
speeds. Therefore, like friction, heat addition also tends to make the Mach
number in the duct approach unity. Cooling causes the Mach number to change in
the direction away from unity.
Rayleigh Flow
Rayleigh
flow refers to adiabetic flow through a constant area duct where the effect of
heat addition or rejection is considered. Compressibility effects often come into
consideration, although the Rayleigh flow model certainly also applies to
incompressible flow. For this model, the duct area remains constant and no mass
is added within the duct. Therefore, unlike Fanno flow, the stagnation
temperature is a variable. The heat addition causes a decrease in stagnation
pressure which is known as the Rayleigh effect and is critical in the design of
combustion systems. Heat addition will cause both supersonic and subsonic Mach
numbers to approach Mach 1, resulting in choked flow. Conversely, heat
rejection decreases a subsonic Mach number and increases a supersonic Mach
number along the duct. It can be shown that for calorically perfect flows the
maximum entropy occurs at M = 1. Rayleigh flow is named after John Strutt, 3rd
Baron Rayleigh.
Theory
The Rayleigh flow model begins with a differential
equation that relates the change in Mach number with the change in stagnation
temperature, T0. The differential
equation is shown below.
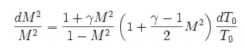
Solving the differential equation leads to the relation
shown below, where T0* is the stagnation temperature at the throat location of the
duct which is required for thermally choking the flow.
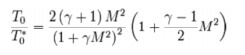
Fundamental Equations
The
following fundamental equations will be used to determine the variation of flow
parameters in Rayleigh flows.
Continuity equation
We know that
Mass flow rate,
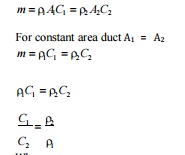
Where ;-
C1
–Velocity of fluid at inlet-m/s
C2
–Velocity of fluid at outlet-m/s
- Density of fluid at
inlet-kg/m3
- Density
of fluid at out let-kg/m3
Momentum equation
Momentum equation between
state 1nad 2 is given by p1 A mc1 p2
A mc2
P1 A P2 A mc2 mc1
P1 P2 A m
c2 c1

Ø Mach Number
The Mach number at the two states are





Stagnation Pressue
Stagnation Temperature
Expression
for Heat Transfer we have
Q mcp T02 T01
the condition 1 is fixed but
the value of T02
attains its maximum when T02 = T0*
Problems based on Rayleigh
flow
1.The
condition of gas in a combustion chamber at entry are M1=0.28, T01=380 K,
P01=4.9 bar. The heat supplied in the combustion chamber is 620 kJ/kg.Determine
Mach number, pressure and temperature of the gas at exit and also determine the
stagnation pressure loss during heating. Take γ= 1.3, cp=1.22 kJ/Kg K.
Given,
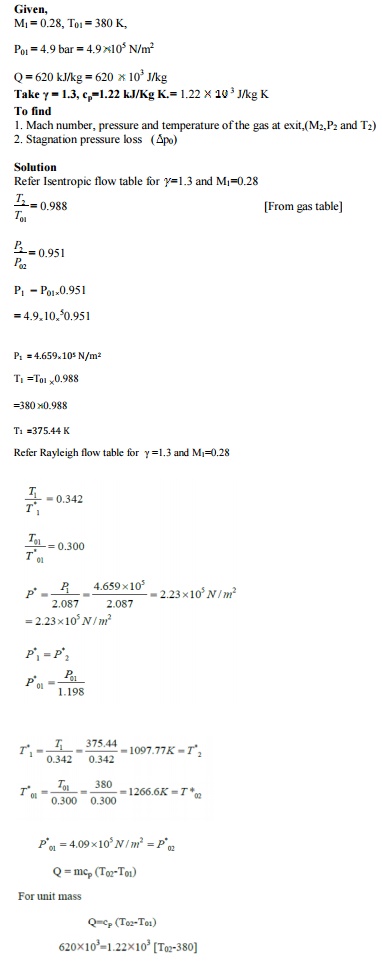

2.A
gas (γ=1.3 and R = 0.46 KJ / Kg K) at a pressure of 70 Kpa and temperature of
295 K enters a combustion chamber at a velocity of 75 m / sec. The heat supplied
in a combustion chamber is 1250 KJ / Kg .Determine the Mach number, pressure
and temperature of gas at exit.
Given:γ=1.3: R = 0.46 KJ / Kg K -1= 70 Kpa :
T1 =295 K C1 = 75 m/sec: Q = 1250 KJ / Kg

Related Topics