Fanno line or Fanno curve (Governing equation)

Fanno line or Fanno curve (Governing equation)

Flow in a constant area duct with friction and without heat transfers is described by a curve is known as Fanno line or Fanno curve.

Weknow that,

From continuity equation,

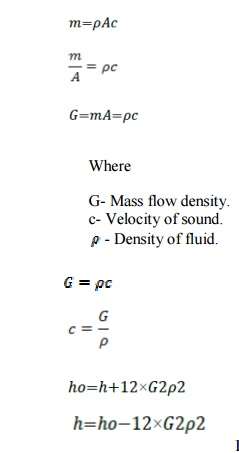
Density ρ is a function of entropy and enthalpy.

Substitute the value for ρinthe equation for ‘h’

The above equation can be used to show a fanno-line in h-s diagram.

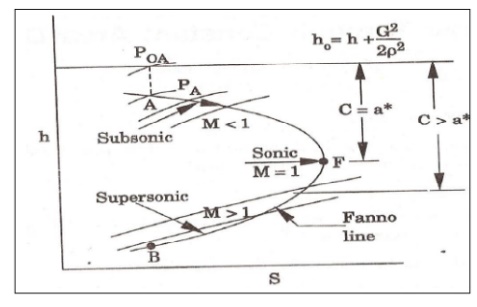
In the line

Ø  Point F is the sonic point

Ø  Point lying below are super sonic points

Ø  Points lying above are subsonic flow

Since entropy can only increase the processes that happen will always coverage to the sonic point F.The curve consists of two branches AF and FB. At point F the flow is sonic i,e, M=1

The flow A to F is subsonic (M<1) and B to F is Supersonic (M>1 )

In subsonic flow region (A to F), the effect of friction will increase the velocity and Mach number and to decrease the enthalpy and pressure of the gas.

In supersonic flow region (B to F), the effect of friction will decrease the velocity and Mach number and to increase the enthalpy and pressure of the gas.

We know by the second law o thermodynamics that for an adiabatic flow, the entropy may increase but cannot decrease. So the processes in the direction F to A and F to B are not possible because they lead to decrease in entropy.

Fanno curves are drawn for different vales of mass flow density (G).When G increases, the velocity increases and pressure decreases in the sub sonic region. When G increases, the pressure increases and velocity decreases in the super sonic region

Important features of Fanno curve

From the second law of thermodynamics, the entropy of the adiabatic flow increases but not decreases. Thus, the path of states along the Fanno curve must be toward the right.

In  the  subsonic  region,  the        effects  of  friction  will  be    to  increase  the velocity and Mach number and         to decrease the enthalpy and       pressure of the stream .

In the supersonic region, the effects of friction will be to decrease the velocity andMach number and to increase the enthalpy and pressure of the stream.

A subsonic flow can never become       supersonic, due to the limitation of second law of thermodynamics, but in can approach to sonic i.e,M=1.

A  supersonic  flow  can  never     become  subsonic,  unless  a  discontinuity (shock)is present.    

In the case of isentropic stagnation, pressure is reduced whether the flow is subsonic or supersonic.