Properties of Laser

Properties of Laser

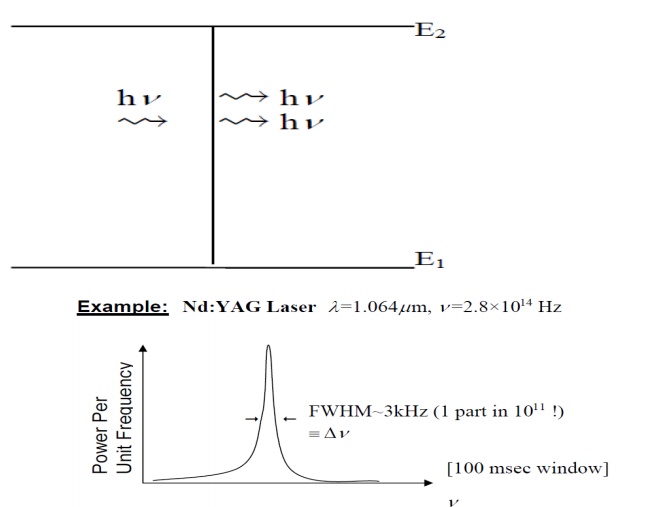
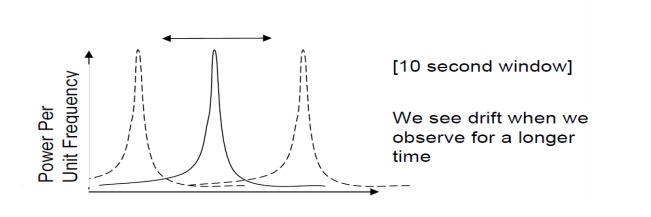
1. Monochromaticity:

This property is due to the following two factors.

First, only an EM wave of frequency n0= (E2-E1)/h can be amplified, n0has a certain range which is called linewidth, this linewidth is decided by homogeneous broadening factors and inhomogeneous broadening factors, the result linewidth is very small compared with normal lights. Second, the laser cavity forms a resonant system, oscillation can occur only at the resonance frequencies of this cavity. This leads to the further narrowing of the laser linewidth, the narrowing can be as large as 10 orders of magnitude! So laser light is usually very pure in wavelength, we say it has the property of monochromaticity.

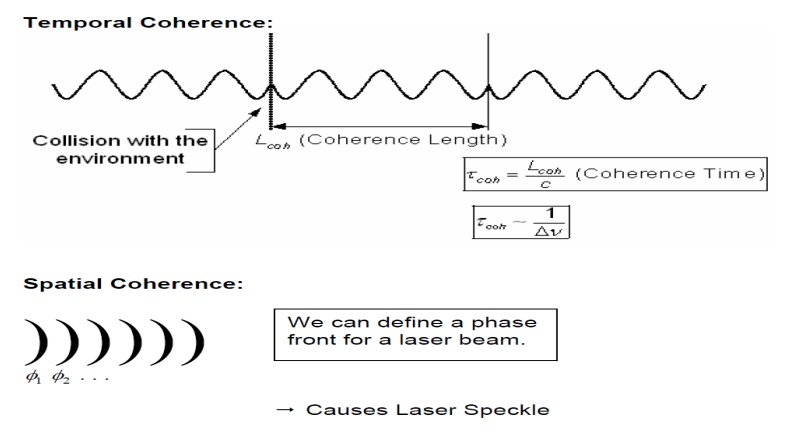
2. Coherence:

For any EM wave, there are two kinds of coherence, namely spatial and temporal coherence.

Let’s consider two points that, at time t=0, lie on the same wave front of some given EM wave, the phase difference of EM wave at the two points at time t=0 is k0. If for any time

t>0 the phase difference of EM wave at the two points remains k0, we say the EM wave has perfect coherence between the two points. If this is true for any two points of the wave front, we say the wave has perfect spatial coherence. In practical the spatial coherence occurs only in a limited area, we say it is partial spatial coherence.

Now consider a fixed point on the EM wave front. If at any time the phase difference between time t and time t+dt remains the same, where "dt" is the time delay period, we say that the EM wave has temporal coherence over a time dt. If dt can be any value, we say the EM wave has perfect temporal coherence. If this happens only in a range 0<dt<t0, we say it has partial temporal coherence, with a coherence time equal to t0. We emphasize here that spatial and temporal coherence are independent. A partial temporal coherent wave can be perfect spatial coherent. Laser light is highly coherent, and this property has been widely used in measurement, holography, etc.

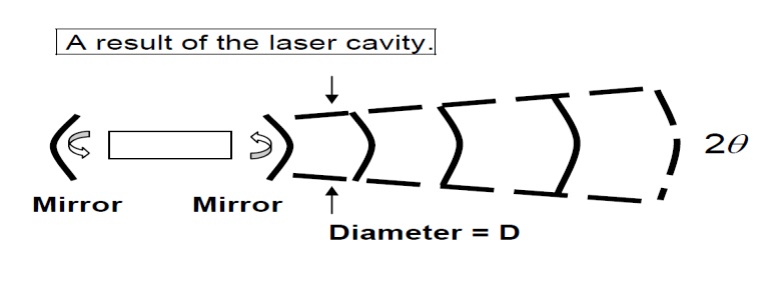
3.Divergence and Directionality:

Laser beam is highly directional, which implies laser light is of very small divergence. This is a direct consequence of the fact that laser beam comes from the resonant cavity, and only waves propagating along the optical axis can be sustained in the cavity. The directionality is described by the light beam divergence angle. Please try the figure below to see the relationship between divergence and optical systems. For perfect spatial coherent light, a beam of aperture diameter D will have unavoidable divergence because of diffraction. From diffraction theory, the divergence angle qd is: qd= b l /D Where l and D are the wavelength and the diameter o

f the beam respectively, b is a coefficient whose value is around unity and depends on the type of light amplitude distribution and the definition of beam diameter. qd is called diffraction limited divergence. If the beam is partial spatial coherent , its divergence is bigger than the diffraction limited divergence. In this case the divergence becomes:

q = b l /(S_c)^1/2

whereS_c is the coherence area.

4. Brightness:

The brightness of a light source is defined as the power emitted per unit surface area per unit solid angle. A laser beam of power P, with a circular beam cross section of diameter D and a divergence angle q and the result emission solid angle is p q 2, then the brightness of laser beam is:

B=4P/(p Dq )²

The max brightness is reached when the beam is perfect spatial coherent.

Bmax=4P/(p l b )2

In case of limited diffraction (q d= l b /D, D=l b /q d, q d=q )