Introduction, Definition, Formula, Solved Example Problems, Exercise | Mathematics - Permutations | 11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra
Permutations
Permutations
1. Factorial
For any natural number n, n factorial is the
product of the first n natural numbers and is denoted by n! or ![]()



2. Fundamental principle of counting
Multiplication principle of counting:
Consider the following situation in an
auditorium which has three entrance doors and two exit doors. Our objective is
to find the number of ways a person can enter the hall and then come out.
Assume that, P1, P2
and P3 are the three
entrance doors and S1 and S2 are the two exit doors. A
person can enter the hall through any one of the doors P1, P2
or P3 in 3 ways. After
entering the hall, the person can come out through any of the two exit doors S1 or S 2 in 2 ways.
Hence the total number of ways of entering the
hall and coming out is
3 x 2 = 6 ways.
These possibilities are explained in the given
flow chart (Fig. 2.1).
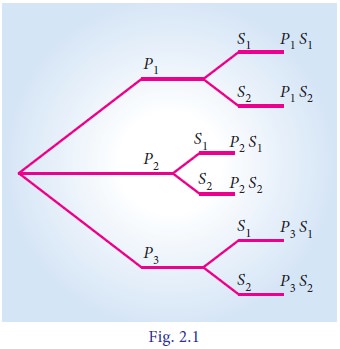
The above problem can be solved by applying
multiplication principle of counting.
Example 2.11
Find the number of 4 letter words, with or
without meaning, which can be formed out of the letters of the word “ NOTE”,
where the repetition of the letters is not allowed.
Solution
Let us allot four vacant places (boxes) to
represent the four letters. N,O,T,E of the given word NOTE.

The first place can be filled by any one of the
4 letters in 4 ways. Since repetition is not allowed, the number of ways of
filling the second vacant place by any of the remaining 3 letters in 3 ways. In
the similar way the third box can be filled in 2 ways and that of last box can
be filled in 1 way. Hence by multiplication principle of counting, total number
of words formed is 4 x 3 x 2 x 1 = 24 words.
Example 2.12
If each objective type questions having 4
choices, then find the total number of ways of answering the 4 questions.
Solution
Since each question can be answered in 4 ways,
the total number of ways of answering 4 questions = 4 x 4 x 4 x 4 =256 ways.
Example 2.13
How many 3 digits numbers can be formed if the
repetition of digits is not allowed?
Solution
Let us allot 3 boxes to represent the digits of
the 3 digit number

Three digit number never begins with “0”. `
100’s place can be filled with any one of the digits from 1 to 9 in 9 ways.
Since repetition is not allowed, 10’s place can
be filled by the remaining 9 numbers (including 0) in 9 ways and the unit place
can be filled by the remaining 8 numbers in 8 ways. Then by multiplication
principle of counting, number of 3 digit numbers = 9x9x8 = 648.
3. Addition principle of counting
Let us consider the following situation in a
class, there are 10 boys and 8 girls. The class teacher wants to select either
a boy or a girl to represent the class in a function. Our objective is to find
the number of ways that the teacher can select the student. Here the teacher
has to perform either of the following two jobs.
One student can be selected in 10 ways among 10
boys.
One student can be selected in 8 ways among 8
girls
Hence the jobs can be performed in 10 + 8 = 18
ways
This problem can be solved by applying Addition
principle of counting.
Definition 2.2
If there are two jobs, each of which can be performed
independently in m and n ways respectively, then either of the two jobs can be
performed in (m+n) ways. This is called addition principle of counting.
Example 2.14
There are 6 books on commerce and 5 books on
accountancy in a book shop. In how many ways can a student purchase either a
book on commerce or a book on accountancy?
Solution
Out of 6 commerce books, a book can be
purchased in 6 ways.
Out of 5 accountancy books, a book can be
purchased in 5 ways.
Then by addition principle counting the total
number of ways of purchasing any one book is 5+6=11 ways.

4. Permutation
Suppose we have a fruit salad with combination
of “APPLES, GRAPES & BANANAS”. We don’t care what order the fruits are in.
They could also be “bananas, grapes and apples” or “grapes, apples and
bananas”. Here the order of mixing is not important. Any how, we will have the
same fruit salad.
But, consider a number lock with the number
code 395. If we make more than three attempts wrongly, then it locked
permanently. In that situation we do care about the order 395. The lock will
not work if we input 3-5-9 or 9-5-3. The number lock will work if it is exactly
3-9-5. We have so many such situations in our practical life. So we should know
the order of arrangement, called Permutation.
Definition 2.3
The number of arrangements that
can be made out of n things taking r at a time is called the number of
permutation of n things taking r at a time.
For example, the number of three digit numbers
formed using the digits 1, 2, 3 taking all at a time is 6
6 three digit numbers are
123,132,231,213,312,321


Example 2.17
In how many ways 7 pictures can be hung from 5
picture nails on a wall ?
Solution

Example 2.18
Find how many four letter words can be formed
from the letters of the word “LOGARITHMS” ( words are with or without meanings)

Permutation of repeated things:
The number of permutation of n different things taken r at a time, when repetition is allowed
is nr.
Example 2.20
Using 9 digits from 1,2,3,……9, taking 3 digits
at a time, how many 3 digits numbers can be formed when repetition is allowed?


5. Circular permutation
In the last section, we have studied
permutation of n different things
taken all together is n!. Each
permutation is a different arrangement of n things in a row or on a straight
line. These are called Linear permutation. Now we consider the permutation of n things along a circle, called circular permutation.
Consider the four letters A, B, C, D and the
number of row arrangement of these 4 letters can be done in 4! Ways. Of those
4! arrangements, the arrangements ABCD, BCDA, CDAB, DABC are one and the same
when they are arranged along a circle.
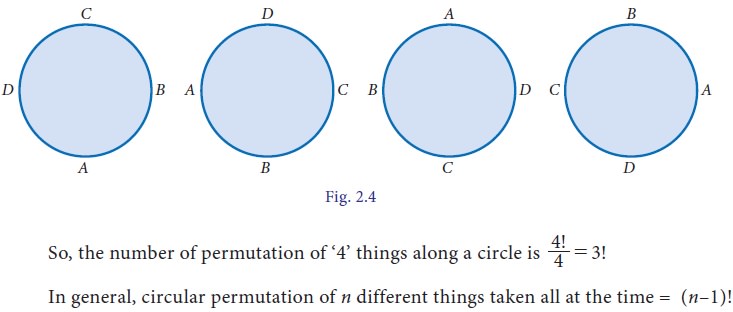




Related Topics