Definition, Formula, Theorem, Solved Example Problems, Exercise | Mathematics - Binomial theorem | 11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra
Binomial theorem
The Binomial theorem or Binomial Expression is a result of expanding the powers of binomials.
Binomial theorem
An algebraic expression of sum or the difference of two terms is called a binomial. For example
are binomials. The Binomial theorem or Binomial Expression is a result of expanding the powers of binomials. It is possible to expand (x + y )n into a sum involving terms of the form axbyc, exponents band c are non-negative integers with b + c = n, the coefficient ‘a’ of each term is a positive integer called binomial coefficient.
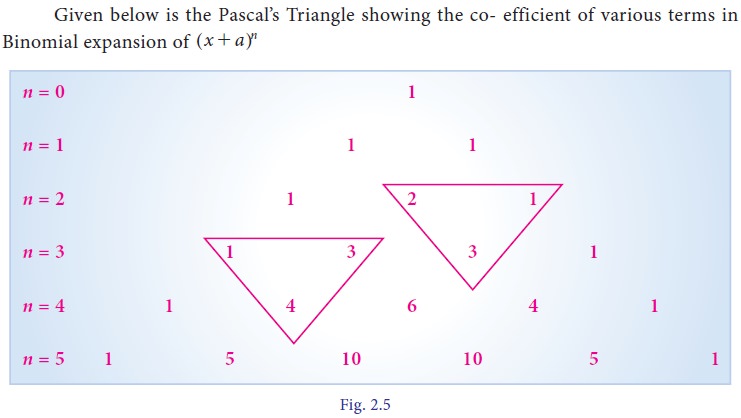
Expansion of (x + a)2 was given by Greek mathematician Euclid on 4th century and there is an evidence that the binomial theorem for cubes i.e., expansion of (x+a)3 was known by 6th century in India. The term Binomial coefficient was first introduced by Michael Stifle in 1544.Blaise Pascal (19 June 1623 to 19 August 1662) a French Mathematician, Physicist, inventor, writer and catholic theologian. In his Treatise on Arithmetical triangle of 1653 described the convenient tabular presentation for Binomial coefficient now called Pascal’s triangle. Sir Issac Newton generalized the Binomial theorem and made it valid for any rational exponent.
Now we study the Binomial theorem for (x + a)n
Sometimes we need a particular term in the expansion of (x + a)n. For this we first write the general term tr +1 . The value of r can be obtained by taking the term tr + 1 as the required term. To find the term independent of x (term without x), equate the power of x in tr + 1 to zero, we get the value of ‘r’. By substituting the value of r in tr + 1 , we get the term independent of x.
An algebraic expression of sum or the difference of two terms is called a binomial. For example
are binomials. The Binomial theorem or Binomial Expression is a result of expanding the powers of binomials. It is possible to expand (x + y )n into a sum involving terms of the form axbyc, exponents band c are non-negative integers with b + c = n, the coefficient ‘a’ of each term is a positive integer called binomial coefficient.Expansion of (x + a)2 was given by Greek mathematician Euclid on 4th century and there is an evidence that the binomial theorem for cubes i.e., expansion of (x+a)3 was known by 6th century in India. The term Binomial coefficient was first introduced by Michael Stifle in 1544.Blaise Pascal (19 June 1623 to 19 August 1662) a French Mathematician, Physicist, inventor, writer and catholic theologian. In his Treatise on Arithmetical triangle of 1653 described the convenient tabular presentation for Binomial coefficient now called Pascal’s triangle. Sir Issac Newton generalized the Binomial theorem and made it valid for any rational exponent.
Now we study the Binomial theorem for (x + a)n
Sometimes we need a particular term in the expansion of (x + a)n. For this we first write the general term tr +1 . The value of r can be obtained by taking the term tr + 1 as the required term. To find the term independent of x (term without x), equate the power of x in tr + 1 to zero, we get the value of ‘r’. By substituting the value of r in tr + 1 , we get the term independent of x.
Tags : Definition, Formula, Theorem, Solved Example Problems, Exercise | Mathematics , 11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra : Binomial theorem | Definition, Formula, Theorem, Solved Example Problems, Exercise | Mathematics
Related Topics
11th Business Mathematics and Statistics(EMS) : Chapter 2 : Algebra