P , NP , and NP-Complete Problems

P , NP , and NP-Complete Problems

In the study of the computational complexity of problems, the first concern of both computer scientists and computing professionals is whether a given problem can be solved in polynomial time by some algorithm.

DEFINITION 1 We say that an algorithm solves a problem in polynomial time if its worst-case time efficiency belongs to O(p(n)) where p(n) is a polynomial of the problem’s input size n. (Note that since we are using big-oh notation here, problems solvable in, say, logarithmic time are solvable in polynomial time as well.) Problems that can be solved in polynomial time are called tractable, and problems that cannot be solved in polynomial time are called intractable.

There are several reasons for drawing the intractability line in this way. First, the entries of Table 2.1 and their discussion in Section 2.1 imply that we cannot solve arbitrary instances of intractable problems in a reasonable amount of time unless such instances are very small. Second, although there might be a huge difference between the running times in O(p(n)) for polynomials of drastically different degrees, there are very few useful polynomial-time algorithms with the degree of a polynomial higher than three. In addition, polynomials that bound running times of algorithms do not usually have extremely large coefficients. Third, polynomial functions possess many convenient properties; in particular, both the sum and composition of two polynomials are always polynomials too. Fourth, the choice of this class has led to a development of an extensive theory called computational complexity, which seeks to classify problems according to their inherent difficulty. And according to this theory, a problem’s intractability

remains the same for all principal models of computations and all reasonable input-encoding schemes for the problem under consideration.

We just touch on some basic notions and ideas of complexity theory in this section. If you are interested in a more formal treatment of this theory, you will have no trouble finding a wealth of textbooks devoted to the subject (e.g., [Sip05], [Aro09]).

P and NP Problems

Most problems discussed in this book can be solved in polynomial time by some algorithm. They include computing the product and the greatest common divisor of two integers, sorting a list, searching for a key in a list or for a pattern in a text string, checking connectivity and acyclicity of a graph, and finding a minimum spanning tree and shortest paths in a weighted graph. (You are invited to add more examples to this list.) Informally, we can think about problems that can be solved in polynomial time as the set that computer science theoreticians call P . A more formal definition includes in P only decision problems, which are problems with yes/no answers.

DEFINITION 2 Class P is a class of decision problems that can be solved in polynomial time by (deterministic) algorithms. This class of problems is called polynomial.

The restriction of P to decision problems can be justified by the following reasons. First, it is sensible to exclude problems not solvable in polynomial time because of their exponentially large output. Such problems do arise naturally— e.g., generating subsets of a given set or all the permutations of n distinct items— but it is apparent from the outset that they cannot be solved in polynomial time. Second, many important problems that are not decision problems in their most natural formulation can be reduced to a series of decision problems that are easier to study. For example, instead of asking about the minimum number of colors needed to color the vertices of a graph so that no two adjacent vertices are colored the same color, we can ask whether there exists such a coloring of the graph’s vertices with no more than m colors for m = 1, 2, . . . . (The latter is called the m-coloring problem.) The first value of m in this series for which the decision problem of m-coloring has a solution solves the optimization version of the graph-coloring problem as well.

It is natural to wonder whether every decision problem can be solved in polynomial time. The answer to this question turns out to be no. In fact, some decision problems cannot be solved at all by any algorithm. Such problems are called undecidable, as opposed to decidable problems that can be solved by an algorithm. A famous example of an undecidable problem was given by Alan Turing in 1936.¹ The problem in question is called the halting problem: given a computer program and an input to it, determine whether the program will halt on that input or continue working indefinitely on it.

Here is a surprisingly short proof of this remarkable fact. By way of contra-diction, assume that A is an algorithm that solves the halting problem. That is, for any program P and input I,

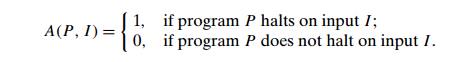
We can consider program P as an input to itself and use the output of algorithm A for pair (P , P ) to construct a program Q as follows:

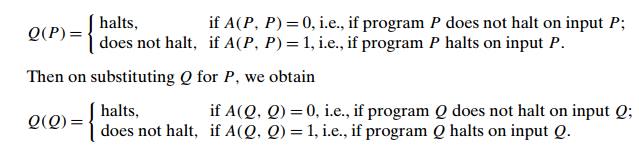
This is a contradiction because neither of the two outcomes for program Q is possible, which completes the proof.

Are there decidable but intractable problems? Yes, there are, but the number of known examples is surprisingly small, especially of those that arise naturally rather than being constructed for the sake of a theoretical argument.

There are many important problems, however, for which no polynomial-time algorithm has been found, nor has the impossibility of such an algorithm been proved. The classic monograph by M. Garey and D. Johnson [Gar79] contains a list of several hundred such problems from different areas of computer science, mathematics, and operations research. Here is just a small sample of some of the best-known problems that fall into this category:

Hamiltonian circuit problem Determine whether a given graph has a Hamiltonian circuit—a path that starts and ends at the same vertex and passes through all the other vertices exactly once.

Traveling salesman problem Find the shortest tour through n cities with known positive integer distances between them (find the shortest Hamiltonian circuit in a complete graph with positive integer weights).

Knapsack problem Find the most valuable subset of n items of given positive integer weights and values that fit into a knapsack of a given positive integer capacity.

Partition problem Given n positive integers, determine whether it is possi-ble to partition them into two disjoint subsets with the same sum. Bin-packing problem Given n items whose sizes are positive rational num-bers not larger than 1, put them into the smallest number of bins of size 1. Graph-coloring problem For a given graph, find its chromatic number, which is the smallest number of colors that need to be assigned to the graph’s vertices so that no two adjacent vertices are assigned the same color.

Integer linear programming problem Find the maximum (or minimum) value of a linear function of several integer-valued variables subject to a finite set of constraints in the form of linear equalities and inequalities.

Some of these problems are decision problems. Those that are not have decision-version counterparts (e.g., the m-coloring problem for the graph-coloring problem). What all these problems have in common is an exponential (or worse) growth of choices, as a function of input size, from which a solution needs to be found. Note, however, that some problems that also fall under this umbrella can be solved in polynomial time. For example, the Eulerian circuit problem—the problem of the existence of a cycle that traverses all the edges of a given graph exactly once—can be solved in O(n²) time by checking, in addition to the graph’s connectivity, whether all the graph’s vertices have even degrees. This example is particularly striking: it is quite counterintuitive to expect that the problem about cycles traversing all the edges exactly once (Eulerian circuits) can be so much easier than the seemingly similar problem about cycles visiting all the vertices exactly once (Hamiltonian circuits).

Another common feature of a vast majority of decision problems is the fact that although solving such problems can be computationally difficult, checking whether a proposed solution actually solves the problem is computationally easy, i.e., it can be done in polynomial time. (We can think of such a proposed solution as being randomly generated by somebody leaving us with the task of verifying its validity.) For example, it is easy to check whether a proposed list of vertices is a Hamiltonian circuit for a given graph with n vertices. All we need to check is that the list contains n + 1 vertices of the graph in question, that the first n vertices are distinct whereas the last one is the same as the first, and that every consecutive pair of the list’s vertices is connected by an edge. This general observation about decision problems has led computer scientists to the notion of a nondeterministic algorithm.

DEFINITION 3 A nondeterministic algorithm is a two-stage procedure that takes as its input an instance I of a decision problem and does the following.

Nondeterministic (“guessing”) stage: An arbitrary string S is generated that can be thought of as a candidate solution to the given instance I (but may be complete gibberish as well).

 Deterministic (“verification”) stage: A deterministic algorithm takes both I and S as its input and outputs yes if S represents a solution to instance I. (If S is not a solution to instance I , the algorithm either returns no or is allowed not to halt at all.)

We say that a nondeterministic algorithm solves a decision problem if and only if for every yes instance of the problem it returns yes on some execu-tion. (In other words, we require a nondeterministic algorithm to be capable of “guessing” a solution at least once and to be able to verify its validity. And, of course, we do not want it to ever output a yes answer on an instance for which the answer should be no.) Finally, a nondeterministic algorithm is said to be nondeterministic polynomial if the time efficiency of its verification stage is polynomial.

Now we can define the class of NP problems.

DEFINITION 4 Class NP is the class of decision problems that can be solved by nondeterministic polynomial algorithms. This class of problems is called nonde-terministic polynomial.

Most decision problems are in NP. First of all, this class includes all the problems in P :

P ⊆ NP.

This is true because, if a problem is in P , we can use the deterministic polynomial-time algorithm that solves it in the verification-stage of a nondeterministic algo-rithm that simply ignores string S generated in its nondeterministic (“guessing”) stage. But NP also contains the Hamiltonian circuit problem, the partition prob-lem, decision versions of the traveling salesman, the knapsack, graph coloring, and many hundreds of other difficult combinatorial optimization problems cataloged in [Gar79]. The halting problem, on the other hand, is among the rare examples of decision problems that are known not to be in NP.

This leads to the most important open question of theoretical computer sci-ence: Is P a proper subset of NP, or are these two classes, in fact, the same? We can put this symbolically as

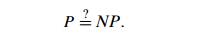
Note that P = NP would imply that each of many hundreds of difficult combinatorial decision problems can be solved by a polynomial-time algorithm, although computer scientists have failed to find such algorithms despite their per-sistent efforts over many years. Moreover, many well-known decision problems are known to be “NP-complete” (see below), which seems to cast more doubts on the possibility that P = NP.

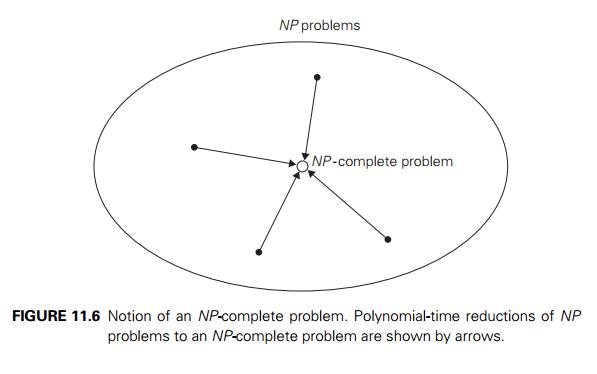
NP -Complete Problems

Informally, an NP-complete problem is a problem in NP that is as difficult as any other problem in this class because, by definition, any other problem in NP can be reduced to it in polynomial time (shown symbolically in Figure 11.6).

Here are more formal definitions of these concepts.

DEFINITION 5 A decision problem D₁ is said to be polynomially reducible to a decision problem D₂, if there exists a function t that transforms instances of D₁ to instances of D₂ such that:

            t maps all yes instances of D₁ to yes instances of D₂ and all no instances of D₁ to no instances of D₂

            t is computable by a polynomial time algorithm

This definition immediately implies that if a problem D₁ is polynomially reducible to some problem D₂ that can be solved in polynomial time, then problem D₁ can also be solved in polynomial time (why?).

DEFINITION 6                 A decision problem D is said to be NP-complete if:

            it belongs to class NP

            every problem in NP is polynomially reducible to D

The fact that closely related decision problems are polynomially reducible to each other is not very surprising. For example, let us prove that the Hamiltonian circuit problem is polynomially reducible to the decision version of the traveling

11.3  P , NP , and NP-Complete Problems

salesman problem. The latter can be stated as the existence problem of a Hamil-tonian circuit not longer than a given positive integer m in a given complete graph with positive integer weights. We can map a graph G of a given instance of the Hamiltonian circuit problem to a complete weighted graph G representing an in-stance of the traveling salesman problem by assigning 1 as the weight to each edge in G and adding an edge of weight 2 between any pair of nonadjacent vertices in G. As the upper bound m on the Hamiltonian circuit length, we take m = n, where n is the number of vertices in G (and G ). Obviously, this transformation can be done in polynomial time.

Let G be a yes instance of the Hamiltonian circuit problem. Then G has a Hamiltonian circuit, and its image in G will have length n, making the image a yes instance of the decision traveling salesman problem. Conversely, if we have a Hamiltonian circuit of the length not larger than n in G , then its length must be exactly n (why?) and hence the circuit must be made up of edges present in G, making the inverse image of the yes instance of the decision traveling salesman problem be a yes instance of the Hamiltonian circuit problem. This completes the proof.

The notion of NP-completeness requires, however, polynomial reducibility of all problems in NP, both known and unknown, to the problem in question. Given the bewildering variety of decision problems, it is nothing short of amazing that specific examples of NP-complete problems have been actually found. Neverthe-less, this mathematical feat was accomplished independently by Stephen Cook in the United States and Leonid Levin in the former Soviet Union.² In his 1971 paper, Cook [Coo71] showed that the so-called CNF-satisfiability problem is NP-complete. The CNF-satisfiability problem deals with boolean expressions. Each boolean expression can be represented in conjunctive normal form, such as the following expression

The CNF-satisfiability problem asks whether or not one can assign values true and false to variables of a given boolean expression in its CNF form to make the entire expression true. (It is easy to see that this can be done for the above formula: if x₁ = true, x₂ = true, and x₃ = false, the entire expression is true.)

Since the Cook-Levin discovery of the first known NP-complete problems, computer scientists have found many hundreds, if not thousands, of other exam-ples. In particular, the well-known problems (or their decision versions) men-tioned above—Hamiltonian circuit, traveling salesman, partition, bin packing, and graph coloring—are all NP-complete. It is known, however, that if P  = NP there must exist NP problems that neither are in P nor are NP-complete.

For a while, the leading candidate to be such an example was the problem of determining whether a given integer is prime or composite. But in an im-portant theoretical breakthrough, Professor Manindra Agrawal and his students Neeraj Kayal and Nitin Saxena of the Indian Institute of Technology in Kanpur announced in 2002 a discovery of a deterministic polynomial-time algorithm for primality testing [Agr04]. Their algorithm does not solve, however, the related problem of factoring large composite integers, which lies at the heart of the widely used encryption method called the RSA algorithm [Riv78].

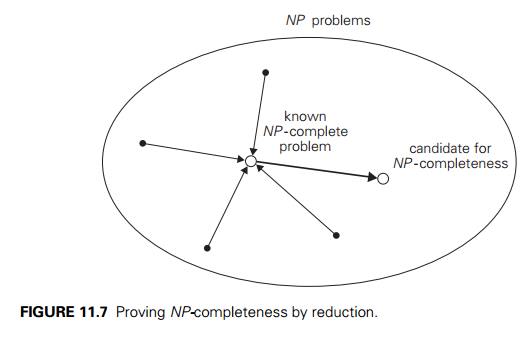
Showing that a decision problem is NP-complete can be done in two steps. First, one needs to show that the problem in question is in NP; i.e., a randomly generated string can be checked in polynomial time to determine whether or not it represents a solution to the problem. Typically, this step is easy. The second step is to show that every problem in NP is reducible to the problem in question in polynomial time. Because of the transitivity of polynomial reduction, this step can be done by showing that a known NP-complete problem can be transformed to the problem in question in polynomial time (see Figure 11.7). Although such a transformation may need to be quite ingenious, it is incomparably simpler than proving the existence of a transformation for every problem in NP. For example, if we already know that the Hamiltonian circuit problem is NP-complete, its polynomial reducibility to the decision traveling salesman problem implies that the latter is also NP-complete (after an easy check that the decision traveling salesman problem is in class NP).

The definition of NP-completeness immediately implies that if there exists a deterministic polynomial-time algorithm for just one NP-complete problem, then every problem in NP can be solved in polynomial time by a deterministic algo-rithm, and hence P = NP. In other words, finding a polynomial-time algorithm

for one NP-complete problem would mean that there is no qualitative difference between the complexity of checking a proposed solution and finding it in polyno-mial time for the vast majority of decision problems of all kinds. Such implications make most computer scientists believe that P  = NP, although nobody has been successful so far in finding a mathematical proof of this intriguing conjecture. Sur-prisingly, in interviews with the authors of a book about the lives and discoveries of 15 prominent computer scientists [Sha98], Cook seemed to be uncertain about the eventual resolution of this dilemma whereas Levin contended that we should expect the P = NP outcome.

?

Whatever the eventual answer to the P = NP question proves to be, knowing that a problem is NP-complete has important practical implications for today. It means that faced with a problem known to be NP-complete, we should probably not aim at gaining fame and fortune³ by designing a polynomial-time algorithm for solving all its instances. Rather, we should concentrate on several approaches that seek to alleviate the intractability of such problems. These approaches are outlined in the next chapter of the book.

 Exercises 11.3

            A game of chess can be posed as the following decision problem: given a legal positioning of chess pieces and information about which side is to move, determine whether that side can win. Is this decision problem decidable?

            A certain problem can be solved by an algorithm whose running time is in O(n^{log2 n}). Which of the following assertions is true?

                                 The problem is tractable.

                                 The problem is intractable.

                                 Impossible to tell.

            Give examples of the following graphs or explain why such examples cannot exist.

                                 graph with a Hamiltonian circuit but without an Eulerian circuit

                                 graph with an Eulerian circuit but without a Hamiltonian circuit

                                 graph with both a Hamiltonian circuit and an Eulerian circuit

                                 graph with a cycle that includes all the vertices but with neither a Hamil-tonian circuit nor an Eulerian circuit

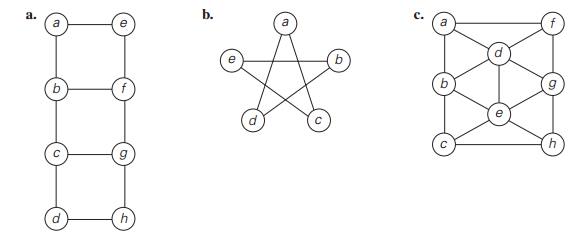
4. For each of the following graphs, find its chromatic number.

            Design a polynomial-time algorithm for the graph 2-coloring problem: deter-mine whether vertices of a given graph can be colored in no more than two colors so that no two adjacent vertices are colored the same color.

            Consider the following brute-force algorithm for solving the composite num-ber problem: Check successive integers from 2 to n/2 as possible divisors of n. If one of them divides n evenly, return yes (i.e., the number is composite); if none of them does, return no. Why does this algorithm not put the problem in class P ?

            State the decision version for each of the following problems and outline a polynomial-time algorithm that verifies whether or not a proposed solution solves the problem. (You may assume that a proposed solution represents a legitimate input to your verification algorithm.)

                                                                                        knapsack problemb. bin packing problem

            Show that the partition problem is polynomially reducible to the decision version of the knapsack problem.

            Show that the following three problems are polynomially reducible to each other.

            Determine, for a given graph G = V , E and a positive integer m ≤ |V |, whether G contains a clique of size m or more. (A clique of size k in a graph is its complete subgraph of k vertices.)

            Determine, for a given graph G = V , E and a positive integer m ≤ |V |, whether there is a vertex cover of size m or less for G. (A vertex cover of size k for a graph G = V , E is a subset V ⊆ V such that |V | = k and, for each edge (u, v) ∈ E, at least one of u and v belongs to V .)

Determine, for a given graph G = V , E and a positive integer m ≤ |V |, whether G contains an independent set of size m or more. (An independent

set of size k for a graph G = V , E is a subset V ⊆ V such that |V | = k and for all u, v ∈ V , vertices u and v are not adjacent in G.)

            Determine whether the following problem is NP-complete. Given several sequences of uppercase and lowercase letters, is it possible to select a letter from each sequence without selecting both the upper- and lowercase versions of any letter? For example, if the sequences are Abc, BC, aB, and ac, it is possible to choose A from the first sequence, B from the second and third, and c from the fourth. An example where there is no way to make the required selections is given by the four sequences AB, Ab, aB, and ab. [Kar86]

Which of the following diagrams do not contradict the current state of our knowledge about the complexity classes P, NP, and NPC (NP-complete problems)?

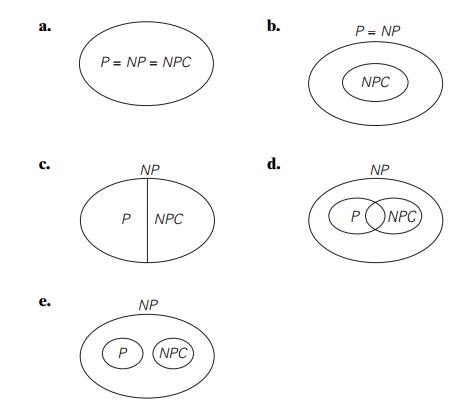
            King Arthur expects 150 knights for an annual dinner at Camelot. Unfortu-nately, some of the knights quarrel with each other, and Arthur knows who quarrels with whom. Arthur wants to seat his guests around a table so that no two quarreling knights sit next to each other.

            Which standard problem can be used to model King Arthur’s task?