Decision Trees algorithms

Decision Trees

            Many important algorithms, especially those for sorting and searching, work by comparing items of their inputs. We can study the performance of such algorithms with a device called a decision tree. As an example, Figure 11.1 presents a decision tree of an algorithm for finding a minimum of three numbers. Each internal node of a binary decision tree represents a key comparison indicated in the node, e.g., k < k . The node’s left subtree contains the information about subsequent comparisons made if k < k , and its right subtree does the same for the case of k > k . (For the sake of simplicity, we assume throughout this section that all input items are distinct.) Each leaf represents a possible outcome of the algorithm’s run on some input of size n. Note that the number of leaves can be greater than the number of outcomes because, for some algorithms, the same outcome can be arrived at through a different chain of comparisons. (This happens to be the case for the decision tree in Figure 11.1.) An important point is that the number of leaves must be at least as large as the number of possible outcomes. The algorithm’s work on a particular input of size n can be traced by a path from the root to a leaf in its decision tree, and the number of comparisons made by the algorithm on such

            a run is equal to the length of this path. Hence, the number of comparisons in the worst case is equal to the height of the algorithm’s decision tree.

        The central idea behind this model lies in the observation that a tree with a given number of leaves, which is dictated by the number of possible outcomes, has to be tall enough to have that many leaves. Specifically, it is not difficult to prove that for any binary tree with l leaves and height h,

Indeed, a binary tree of height h with the largest number of leaves has all its leaves on the last level (why?). Hence, the largest number of leaves in such a tree is 2h. In other words, 2h ≥ l, which immediately implies (11.1).

Inequality (11.1) puts a lower bound on the heights of binary decision trees and hence the worst-case number of comparisons made by any comparison-based algorithm for the problem in question. Such a bound is called the information-theoretic lower bound (see Section 11.1). We illustrate this technique below on two important problems: sorting and searching in a sorted array.

Decision Trees for Sorting

Most sorting algorithms are comparison based, i.e., they work by comparing elements in a list to be sorted. By studying properties of decision trees for such algorithms, we can derive important lower bounds on their time efficiencies.

            We can interpret an outcome of a sorting algorithm as finding a permutation of the element indices of an input list that puts the list’s elements in ascending order. Consider, as an example, a three-element list a, b, c of orderable items such as real numbers or strings. For the outcome a < c < b obtained by sorting this list (see Figure 11.2), the permutation in question is 1, 3, 2. In general, the number of possible outcomes for sorting an arbitrary n-element list is equal to n!.

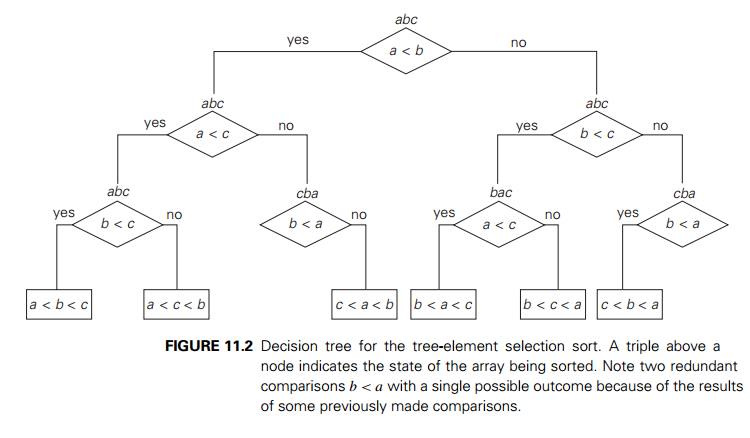
Inequality (11.1) implies that the height of a binary decision tree for any comparison-based sorting algorithm and hence the worst-case number of com-parisons made by such an algorithm cannot be less than | log2 n! |:

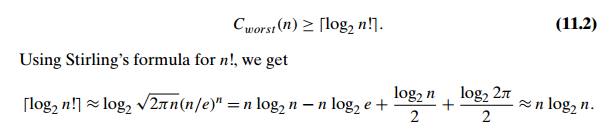
In other words, about n log2 n comparisons are necessary in the worst case to sort an arbitrary n-element list by any comparison-based sorting algorithm. Note that mergesort makes about this number of comparisons in its worst case and hence is asymptotically optimal. This also implies that the asymptotic lower bound n log2 n is tight and therefore cannot be substantially improved. We should point out, however, that the lower bound of log2 n! can be improved for some values of n. For example, log2 12! = 29, but it has been proved that 30 comparisons are necessary (and sufficient) to sort an array of 12 elements in the worst case.

We can also use decision trees for analyzing the average-case efficiencies of comparison-based sorting algorithms. We can compute the average number of comparisons for a particular algorithm as the average depth of its decision tree’s leaves, i.e., as the average path length from the root to the leaves. For example, for

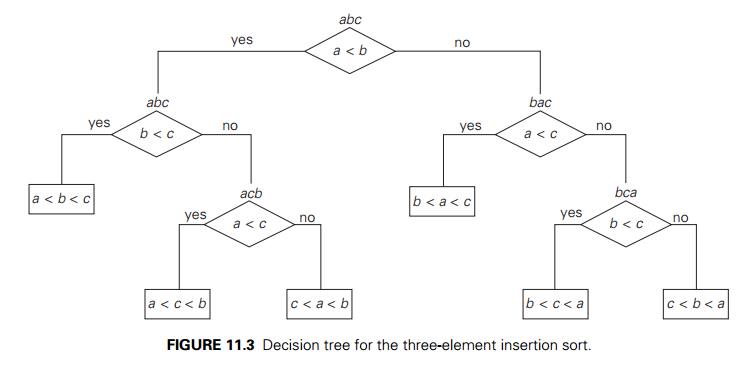
the three-element insertion sort whose decision tree is given in Figure 11.3, this

number is (2 + 3 + 3 + 2 + 3 + 3)/6 = 2 23 .

Under the standard assumption that all n! outcomes of sorting are equally likely, the following lower bound on the average number of comparisons Cavg made by any comparison-based algorithm in sorting an n-element list has been proved:

As we saw earlier, this lower bound is about n log2 n. You might be surprised that the lower bounds for the average and worst cases are almost identical. Remember, however, that these bounds are obtained by maximizing the number of compar-isons made in the average and worst cases, respectively. For a particular sorting algorithm, the average-case efficiency can, of course, be significantly better than their worst-case efficiency.

Decision Trees for Searching a Sorted Array

In this section, we shall see how decision trees can be used for establishing lower bounds on the number of key comparisons in searching a sorted array of n keys: A[0] < A[1] < . . . < A[n − 1]. The principal algorithm for this problem is binary search. As we saw in Section 4.4, the number of comparisons made by binary search in the worst case, Cworstbs (n), is given by the formula

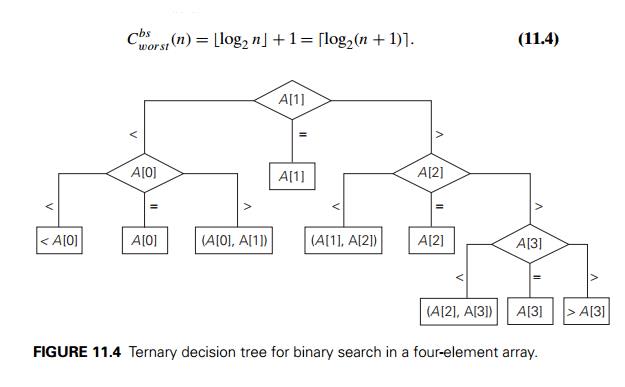
We will use decision trees to determine whether this is the smallest possible number of comparisons.

Since we are dealing here with three-way comparisons in which search key K is compared with some element A[i] to see whether K < A[i], K = A[i], or K > A[i], it is natural to try using ternary decision trees. Figure 11.4 presents such a tree for the case of n = 4. The internal nodes of that tree indicate the array’s elements being compared with the search key. The leaves indicate either a matching element in the case of a successful search or a found interval that the search key belongs to in the case of an unsuccessful search.

We can represent any algorithm for searching a sorted array by three-way comparisons with a ternary decision tree similar to that in Figure 11.4. For an array of n elements, all such decision trees will have 2n + 1 leaves (n for successful searches and n + 1 for unsuccessful ones). Since the minimum height h of a ternary tree with l leaves is log3 l , we get the following lower bound on the number of worst-case comparisons:

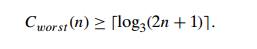
This lower bound is smaller than log2(n + 1) , the number of worst-case comparisons for binary search, at least for large values of n (and smaller than or equal to log2(n + 1) for every positive integer n—see Problem 7 in this section’s exercises). Can we prove a better lower bound, or is binary search far from being optimal? The answer turns out to be the former. To obtain a better lower bound, we should consider binary rather than ternary decision trees, such as the one in Figure 11.5. Internal nodes in such a tree correspond to the same three-way comparisons as before, but they also serve as terminal nodes for successful searches. Leaves therefore represent only unsuccessful searches, and there are n + 1 of them for searching an n-element array.

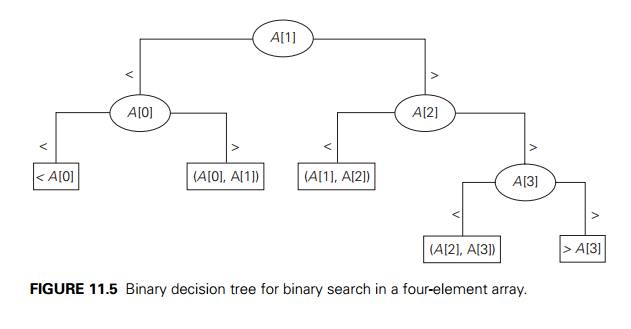
As comparison of the decision trees in Figures 11.4 and 11.5 illustrates, the binary decision tree is simply the ternary decision tree with all the middle subtrees eliminated. Applying inequality (11.1) to such binary decision trees immediately yields

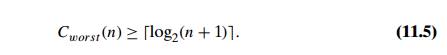
This inequality closes the gap between the lower bound and the number of worst-case comparisons made by binary search, which is also log2(n + 1) . A much more sophisticated analysis (see, e.g., [KnuIII, Section 6.2.1]) shows that under the standard assumptions about searches, binary search makes the smallest number of comparisons on the average, as well. The average number of comparisons made by this algorithm turns out to be about log2 n − 1 and log2(n + 1) for successful and unsuccessful searches, respectively.

Exercises 11.2

            Prove by mathematical induction that

            h ≥  log2 l  for any binary tree with height h and the number of leaves l.

            h ≥  log3 l  for any ternary tree with height h and the number of leaves l.

            Consider the problem of finding the median of a three-element set {a, b, c} of orderable items.

            What is the information-theoretic lower bound for comparison-based al-gorithms solving this problem?

            Draw a decision tree for an algorithm solving this problem.

If the worst-case number of comparisons in your algorithm is greater than the information-theoretic lower bound, do you think an algorithm

matching the lower bound exists? (Either find such an algorithm or prove its impossibility.)

            Draw a decision tree and find the number of key comparisons in the worst and average cases for

            the three-element basic bubble sort.

            the three-element enhanced bubble sort (which stops if no swaps have been made on its last pass).

            Design a comparison-based algorithm for sorting a four-element array with the smallest number of element comparisons possible.

            Design a comparison-based algorithm for sorting a five-element array with seven comparisons in the worst case.

            Draw a binary decision tree for searching a four-element sorted list by sequen-tial search.

            Compare the two lower bounds for searching a sorted array— log3(2n + 1) and log2(n + 1) —to show that

            log3(2n + 1)  ≤  log2(n + 1)  for every positive integer n.

            log3(2n + 1)  <  log2(n + 1)  for every positive integer n ≥ n0.

            What is the information-theoretic lower bound for finding the maximum of n numbers by comparison-based algorithms? Is this bound tight?

            A tournament tree is a complete binary tree reflecting results of a “knockout tournament”: its leaves represent n players entering the tournament, and each internal node represents a winner of a match played by the players represented by the node’s children. Hence, the winner of the tournament is represented by the root of the tree.

            What is the total number of games played in such a tournament?

            How many rounds are there in such a tournament?

            Design an efficient algorithm to determine the second-best player using the information produced by the tournament. How many extra games does your algorithm require?

Advanced fake-coin problem There are n ≥ 3 coins identical in appearance; either all are genuine or exactly one of them is fake. It is unknown whether the fake coin is lighter or heavier than the genuine one. You have a balance scale with which you can compare any two sets of coins. That is, by tipping to the left, to the right, or staying even, the balance scale will tell whether the sets weigh the same or which of the sets is heavier than the other, but not by how much. The problem is to find whether all the coins are genuine and, if not, to find the fake coin and establish whether it is lighter or heavier than the genuine ones.

            Prove that any algorithm for this problem must make at least log3(2n + 1) weighings in the worst case.

            Draw a decision tree for an algorithm that solves the problem for n = 3 coins in two weighings.

            Prove that there exists no algorithm that solves the problem for n = 4 coins in two weighings.

            Draw a decision tree for an algorithm that solves the problem for n = 4 coins in two weighings by using an extra coin known to be genuine.

            Draw a decision tree for an algorithm that solves the classic version of the problem—that for n = 12 coins in three weighings (with no extra coins being used).

            Jigsaw puzzle A jigsaw puzzle contains n pieces. A “section” of the puzzle is a set of one or more pieces that have been connected to each other. A “move” consists of connecting two sections. What algorithm will minimize the number of moves required to complete the puzzle?