Microbial Killing

MICROBIAL KILLING

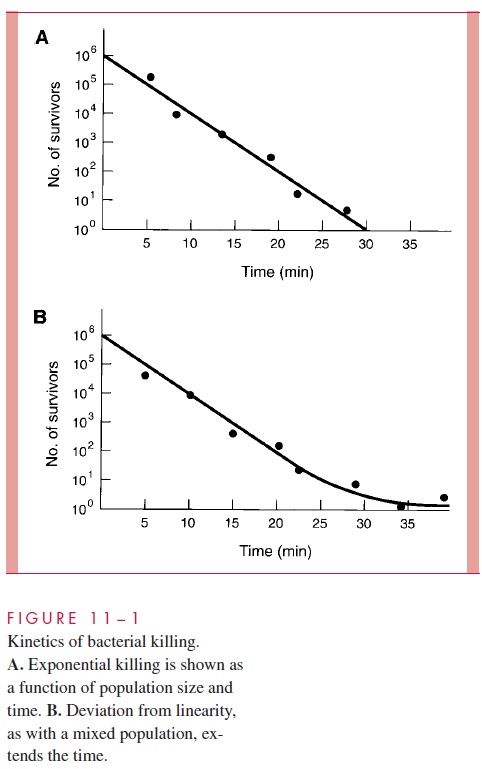
Killing of bacteria by heat, radiation, or chemicals is usually exponential with time; that is, a fixed proportion of survivors are killed during each time increment. Thus, if 90% of a population of bacteria are killed during each 5 minutes of exposure to a weak solution of a disinfectant, a starting population of 106/mL is reduced to 105/mL after 5 minutes, to 103/mL after 15 minutes, and theoretically to 1 organism (100)/mL after 30 minutes. Ex-ponential killing corresponds to a first-order reaction or a “single-hit” hypothesis in which the lethal change involves a single target in the organism, and the probability of this change is constant with time. Thus, plots of the logarithm of the number of survivors against time are linear (Fig 11 – 1A); however, the slope of the curve varies with the effec-tiveness of the killing process, which is influenced by the nature of the organism, lethal agent, concentration (in the case of disinfectants), and temperature. In general, the rate of killing increases exponentially with arithmetic increases in temperature or in concentra-tions of disinfectant.

     An important consequence of exponential killing with most sterilization processes is that sterility is not an absolute term, but must be expressed as a probability. Thus, to con-tinue the example given previously, the chance of a single survivor in 1 mL is theoreti-cally 10 -1 after 35 minutes. If a chance of 10-9 were the maximum acceptable risk for a single surviving organism in a 1-mL sample (eg, of a therapeutic agent), the procedure would require continuation for a total of 75 minutes.

     A simple single-hit curve often does not express the kinetics of killing adequately. In the case of some bacterial endospores, a brief period (activation) may elapse before expo-nential killing by heat begins. If multiple targets are involved, the experimental curve will deviate from linearity. More significant is the fact that microbial populations may include a small proportion of more resistant mutants or of organisms in a physiologic state that confers greater resistance to inactivation. In these cases, the later stages of the curve are flattened (Fig 11 – 1B), and extrapolations from the exponential phase of killing may seriously underestimate the time needed for a high probability of achieving complete sterility. In practice, materials that come into contact with tissues are sterilized under con-ditions that allow a very wide margin of safety, and the effectiveness of inactivation of or-ganisms in vaccines is tested directly with large volumes and multiple samples before a product is made available for use.