Methods Based on Chemical Kinetics: Characterization Applications

Characterization Applications

Chemical kinetic methods also find use in determining rate constants and elucidat- ing reaction mechanisms. These applications are illustrated by two examples from the chemical kinetic analysis of enzymes.

Determining V_max and K_m for Enzyme-Catalyzed Reactions 

The value of V_max and K_m for an enzymatic reaction are of significant interest in the study of cellular chemistry.15 From equation 13.19 we see that V_max provides a means for determin- ing the rate constant k₂. For enzymes that follow the mechanism shown in reaction 13.15, k₂ is equivalent to the enzyme’s turnover number, k_cat. The turnover number is the maximum number of substrate molecules converted to product by a single ac- tive site on the enzyme, per unit time. Thus, the turnover number provides a direct indication of the catalytic efficiency of an enzyme’s active site. The Michaelis con- stant, K_m, is significant because it provides an estimate of the substrate’s intracellu- lar concentration.

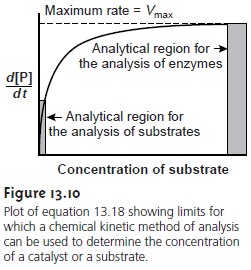
Values of V_max and K_m for reactions obeying the mechanism shown in reaction 13.15 can be determined using equation 13.18 by measuring the rate of reaction as a function of the substrate’s concentration. The curved nature of the relationship be- tween rate and the concentration of substrate (see Figure 13.10), however, is incon- venient for this purpose. Equation 13.18 can be rewritten in a linear form by taking its reciprocal

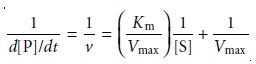
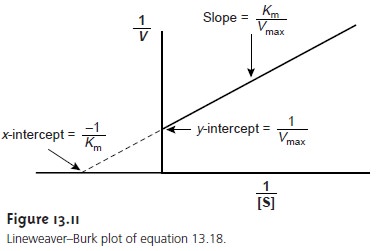
A plot of 1/v versus 1/[S], which is called a double reciprocal, or Lineweaver–Burk plot, is a straight line with a slope of K_m/V_max, a y-intercept of 1/V_max, and an x-intercept of –1/K_m (Figure 13.11).

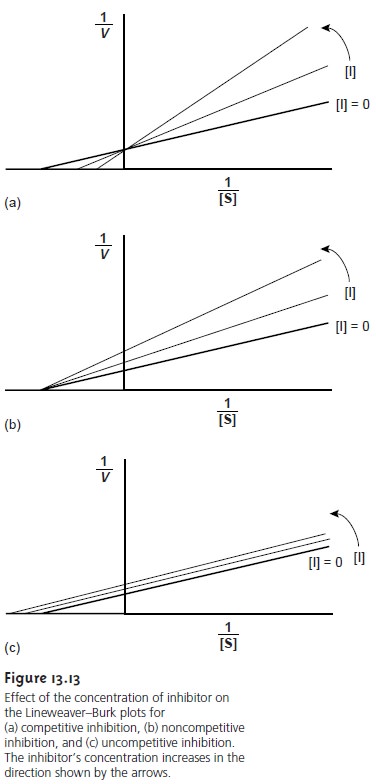
Elucidating Mechanisms for the Inhibition of Enzyme Catalysis 

An inhibitor inter- acts with an enzyme in a manner that decreases the enzyme’s catalytic efficiency. Examples of inhibitors include some drugs and poisons. Irreversible inhibitors co- valently bind to the enzyme’s active site, producing a permanent loss in catalytic ef- ficiency even when the inhibitor’s concentration is decreased. Reversible inhibitors form noncovalent complexes with the enzyme, thereby causing a temporary decrease in catalytic efficiency. If the inhibitor is removed, the enzyme’s catalytic effi- ciency returns to its normal level.

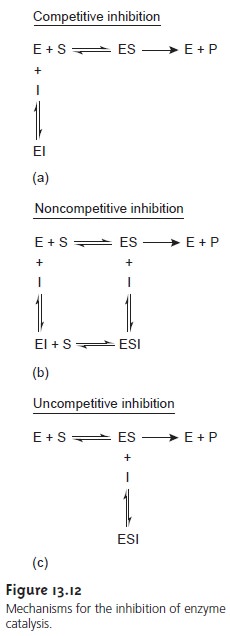
The reversible binding of an inhibitor to an enzyme can occur through several pathways, as shown in Figure 13.12. In competitive inhibition (Figure 13.12a), the substrate and the inhibitor compete for the same active site on the enzyme. Because the substrate cannot bind to an enzyme that is already bound to an inhibitor, the enzyme’s catalytic efficiency for the substrate is decreased. With noncompetitive in- hibition (Figure 13.12b) the substrate and inhibitor bind to separate active sites on the enzyme, forming an enzyme–substrate–inhibitor, or ESI complex. The presence of the ESI complex, however, decreases catalytic efficiency since only the enzyme–substrate complex can react to form product. Finally, in uncompetitive in- hibition (Figure 13.12c) the inhibitor cannot bind to the free enzyme, but can bind to the enzyme–substrate complex. Again, the result is the formation of an inactive ESI complex.

The three reversible mechanisms for enzyme inhibition are distinguished by ob- serving how changing the inhibitor’s concentration affects the relationship between the rate of reaction and the concentration of substrate. As shown in Figure 13.13, when kinetic data are displayed as a Lineweaver–Burk plot, it is possible to determinewhich mechanism is in effect.