Evaluation of Chemical Kinetic Methods

Evaluation of Chemical Kinetic Methods

Scale of Operation 

The detection limit for chemical kinetic methods ranges from minor components to ultratrace components and is principally determined by two factors: the rate of the reaction and the instrumental method used for monitoring the rate. Because the signal is directly proportional to the reaction rate, faster reactions generally result in lower detection limits. All other considerations being equal, the detection limit is smaller for catalytic reactions than for noncatalytic reactions. Not surprisingly, chemical kinetic methods based on catalysis were among the earliest techniques for trace-level analysis. Ultratrace analysis is also possible when using catalytic reactions. For example, ultratrace levels of Cu (<1 ppb) can be determined by measuring its catalytic effect on the redox re- action between hydroquinone and H₂O₂. Without a catalyst, most chemical kinetic methods for organic compounds involve reactions with relatively slow rates, limit- ing the method to minor and higher concentration trace analytes. Noncatalytic chemical kinetic methods for inorganic compounds involving metal–ligand com- plexation may be fast or slow, with detection limits ranging from trace to minor lev- els of analyte.

The second factor influencing detection limits is the instru- mental method used to monitor the reaction’s progress. Most reactions are monitored spectrophotometrically or electro- chemically.

Accuracy 

As noted earlier, chemical kinetic methods are po- tentially subject to larger errors than equilibrium methods due to the effect of uncontrolled or poorly controlled variables, such as temperature and solution pH. Although the direct- computation chemical kinetic methods described can yield results with moderate accuracy (1–5%), re- action systems are encountered in which accuracy is quite poor. An improvement in accuracy may be realized by using curve-fitting methods. In one study, for example, accuracy was improved by two orders of magnitude (500–5%) by replacing a direct-computation analysis with a curve-fitting analysis. Although not discussed in this, data analy- sis methods that include the ability to compensate for experi- mental error can lead to a significant improvement in accuracy.

Precision 

The precision of a chemical kinetic method is lim- ited by the signal-to-noise ratio of the instrumental method used to monitor the reaction’s progress. With integral methods, precisions of 1–2% are routinely possible. The precision for dif- ferential methods may be somewhat poorer, particularly for noisy signals, due to the difficulty in measuring the slope of a noisy rate curve.19 It may be possible to improve the precision in this case by using a combination of signal averaging and smoothing of the data before its analysis.

Sensitivity 

The sensitivity for a one-point fixed-time integral method of analysis is improved by making measurements under conditions in which the concentration of the monitored species is larger rather than smaller. When the analyte’s concentra- tion, or the concentration of any other reactant, is monitored, measurements are best made early in the reaction before its concentration has substantially decreased. On the other hand, when a product is used to monitor the reaction, measurements are more appropriately made at longer times. For a two-point fixed-time integral method, sensitivity is improved by increasing the difference between times t₁ and t₂. As discussed earlier, the sensitivity of a rate method improves when using the initial rate.

Selectivity 

The analysis of closely related compounds, as we have seen in earlier, is often complicated by their tendency to interfere with one an- other. To overcome this problem, the analyte and interferent must first be sepa- rated. An advantage of chemical kinetic methods is that conditions can often be adjusted so that the analyte and interferent have different reaction rates. If the difference in rates is large enough, one species may react completely before the other species has a chance to react. For example, many enzymes selectively cat- alyze a single substrate, allowing the quantitative analysis of that substrate in the presence of similar substrates.

The conditions necessary to ensure that a faster-reacting species can be kineti- cally separated from a more slowly reacting species can be determined from the ap- propriate integrated rate laws. As an example, let’s consider a system consisting of an analyte, A, and an interferent, B, both of which show first-order kinetics with a common reagent. To avoid an interference, the relative magnitudes of their rate constants must be sufficiently different. The fractions, f, of A and B remaining at any point in time, t, are given as

For a first-order reaction we can write, from equations 13.2, 13.21, and 13.22

ln(f_A)_t = –k_At

ln(f_B)_t = –k_Bt

Taking the ratio of these two equations gives

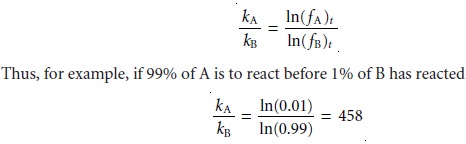
then the rate constant for A must be 458 times larger than that for B. Under these conditions the analyte’s concentration can be determined before the interferent be- gins to react. If the analyte has the slower reaction, then it can be determined after the interferent’s reaction is complete.

The method described here is impractical when the simultaneous analysis of both A and B is desired. The difficulty in this case is that conditions favoring the analysis of A generally do not favor the analysis of B. For example, if condi- tions are adjusted such that 99% of A reacts in 5 s, then B must reach 99% com- pletion in either 0.01 s if it has the faster kinetics or 2300 s if it has the slower kinetics.

Several additional approaches for analyzing mixtures have been developed that do not require such a large difference in rate constants.3,4 Because both A and B react at the same time, the integrated form of the first-order rate law becomes

C_t = [A]_t + [B]_t = [A]₀e–kAt + [B]₀e–kBt ………………….13.23

where C_t is the total concentration of A and B. If C_t is measured at times t₁ and t₂, the resulting pair of simultaneous equations can be solved to give [A]₀ and [B]₀. The rate constants k_A and k_B must be determined in separate experiments using standard solutions of A and B. Alternatively, if A and B react to form a common product, P, equation 13.23 can be written as

P_t = [A]₀(1 – e–kAt) + [B]₀(1 – e–kBt)

Again, a pair of simultaneous equations at times t₁ and t₂ can be solved for [A]₀ and [B]₀.

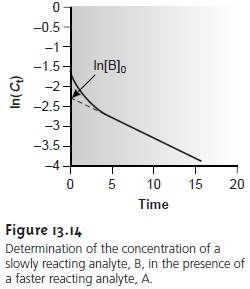
Equation 13.23 can also be used as the basis for a curve-fitting method. As shown in Figure 13.14, a plot of ln(C_t) as a function of time consists of two regions. At short times the plot is curved since A and B are reacting simultaneously. At later times, however, the concentration of the faster-reacting component, A, decreases to 0, and equation 13.23 simplifies to

Under these conditions a plot of ln(C_t) versus time is linear. Extrapolating the linear portion to time 0 gives [B]₀, and [A]₀ is determined by difference.

Time, Cost, and Equipment 

Automated chemical kinetic methods of analysis provide a rapid means for analyzing samples, with throughputs ranging from several hundred to several thousand determinations per hour. The initial start-up costs, however, may be fairly high because an automated analysis requires a dedicated in- strument designed to meet the specific needs of the analysis. When handled manu- ally, chemical kinetic methods can be accomplished using equipment and instru- mentation routinely available in most laboratories. Sample throughput, however, is much lower than with automated methods.