Linear block and Hamming codes

Block Codes:

Block codes operate on a block of bits.Block codes are referred to as (n, k) codes. A block of k information bits are coded to become a block of n bits. But before we go any further with the details, let‟s look at an important concept in coding called Hamming distance. Let‟s say that we want to code the 10 integers, 0 to 9 by a digital sequence. Sixteen unique sequences can be obtained from four bit words. We assign the first ten of these, one to each integer. Each integer is now identified by its own unique sequence of bits.

Hamming Weight: The Hamming weight of this code scheme is the largest number of 1‟s ina valid codeword. This number is 3 among the 10 codewords we have chosen. (the ones in the while space).

Concept of Hamming Distance: In continuous variables, we measure distance by Euclidean concepts such as lengths, angles and vectors.In the binary world, distances are measured between two binary words by something called the Hamming distance. The Hamming distance is the number of disagreements between two binary sequences of the same size. The Hamming distance between sequences 001 and 101 is = 1 The Hamming distance between sequences 0011001 and 1010100 is = 4. Hamming distance and weight are very important and useful concepts in coding. The knowledge of Hamming distance is used to determine the capability of a code to detect and correct errors. Although the Hamming weight of our chosen code set is 3, the minimum Hamming distance is 1. We can generalize this to say that the maximum number of error bits that can be detected is

t = dmin –1

Where dmin is Hamming distance of the codewords. For a code with dmin = 3, we can both detect 1 and 2 bit errors. So we want to have a code set with as large a Hamming distance as possible since this directly effects our ability to detect errors. The number of errors that we can correct is given by

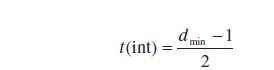
Creating block codes: The block codes are specified by (n.k). The code takes k informationbits and computes (n-k) parity bits from the code generator matrix. Most block codes are systematic in that the information bits remain unchanged with parity bits attached either to the front or to the back of the information sequence.

*  Hamming code, a simple linear block code

*  Hamming codes are most widely used linear block codes.

*  A Hamming code is generally specified as (2n- 1, 2n-n-1).

*  The size of the block is equal to 2n-1.

*  The number of information bits in the block is equal to 2n-n-1 and the number of overhead bits is equal to n. All Hamming codes are able to detect three errors and correct one.

Reed-Solomon Codes: Reed Solomon (R-S) codes form an important sub-class of the familyof Bose- Chaudhuri-Hocquenghem (BCH) codes and are very powerful linear non-binary block codes capable of correcting multiple random as well as burst errors. They have an important feature that the generator polynomial and the code symbols are derived from the same finite field. This enables to reduce the complexity and also the number of computations involved in their implementation. A large number of R-S codes are available with different code rates.

An R-S code is described by a generator polynomial g(x) and other usual important code parameters such as the number of message symbols per block (k), number of code symbols per block (n), maximum number of erroneous symbols (t) that can surely be corrected per block of received symbols and the designed minimum symbol Hamming distance (d). A parity-check polynomial h (X) of order k also plays a role in designing the code. The symbol x, used in polynomials is an indeterminate which usually implies unit amount of delay.

For positive integers m and t, a primitive (n, k, t) R-S code is defined as below: Number of encoded symbols per block: n = 2m – 1 Number of message symbols per block: k Code rate: R= k/n Number of parity symbols per block: n – k = 2t Minimum symbol Hamming distance per block: d = 2t +1. It can be noted that the block length n of an (n, k, t) R-S code is bounded by the corresponding finite field GF(2m). Moreover, as n – k = 2t, an (n, k, t) R-S code has optimum error correcting capability.