Chapter: Digital Communication : Error Control Coding
Convolutional codes
Convolutional codes:
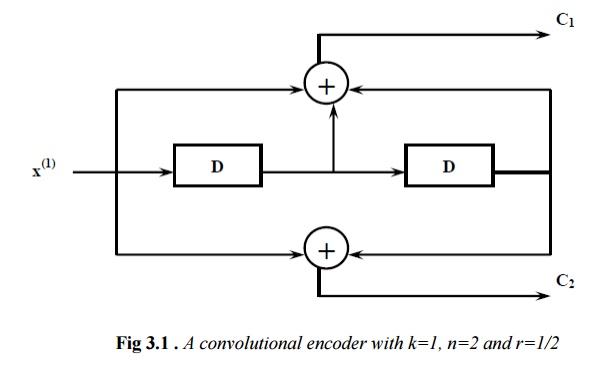
*Convolutional codes are widely used as channel codes in practical communication systems for error correction. *The encoded bits depend on the current k input bits and a few past input bits. * The main decoding strategy for convolutional codes is based on the widely used Viterbi algorithm. *Convolutional codes are commonly described using two parameters: the code rate and the constraint length. The code rate, k/n, is expressed as a ratio of the number of bits into the convolutional encoder (k) to the number of channel symbols output by the convolutional encoder (n) in a given encoder cycle. *The constraint length parameter, K, denotes the "length" of the convolutional encoder, i.e. how many k-bit stages are available to feed the combinatorial logic that produces the output symbols. Closely related to K is the parameter m, which can be thought of as the memory length of the encoder. A simple convolutional encoder is shown below(fig.). The information bits are fed in small groups of k-bits at a time to a shift register. The output encoded bits are obtained by modulo-2 addition (EXCLUSIVE-OR operation) of the input information bits and the contents of the shift registers which are a few previous information bits.
The operation of a convolutional encoder can be explained in several but equivalent ways such as, by
a) state diagram representation.
b) Tree diagram representation.
c) trellis diagram representation.
a) State Diagram Representation:
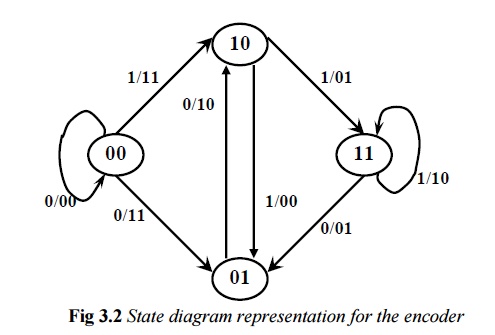
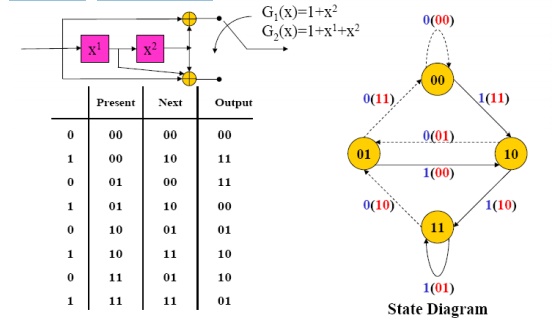
A convolutional encoder may be defined as a finite statemachine. Contents of the rightmost (K-1) shift register stages define the states of the encoder. So, the encoder in Fig. 3.1 has four states. The transition of an encoder from one state to another, as caused by input bits, is depicted in the state diagram.Fig. 3.2shows the state diagram of the encoder in Fig. 3.1. A new input bit causes a transition from one state to another
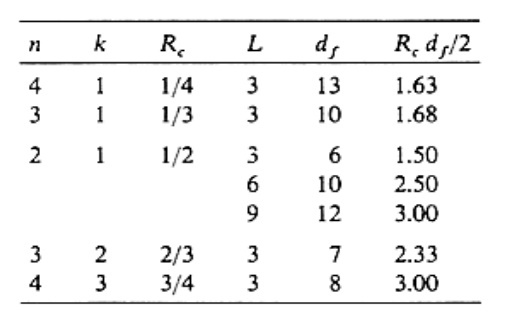
b) Tree Diagram Representation:
The tree diagram representation shows all possibleinformation and encoded sequences for the convolutional encoder. Fig. 3.3 shows the tree diagram for the encoder in Fig. 3.1. The encoded bits are labeled on the branches of the tree. Given an nput sequence, the encoded sequence can be directly read from the tree.
Representing convolutional codes compactly: code trellis and state diagram:
STATE DIAGRAM:
Inspecting state diagram: Structural properties of convolutional codes:
·Each new block of k input bits causes a transition into new state.
·Hence there are 2k branches leaving each state.
· Assuming encoder zero initial state, encoded word for any input of k bits can thus be obtained. For instance, below for u=(1 1 1 0 1), encoded wordv=(1 1, 1 0, 0 1, 0 1, 1 1, 1 0, 1 1, 1 1) is produced:
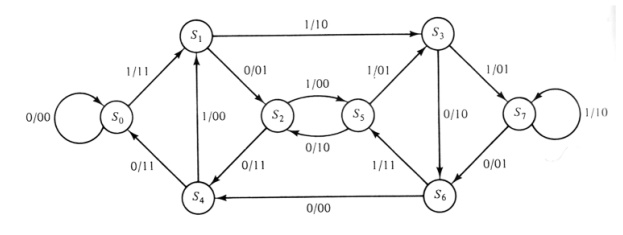
- Encoder state diagram for (n,k,L)=(2,1,2) code
- Note that the number of states is 2L+1 = 8.
Distance for some convolutional codes:
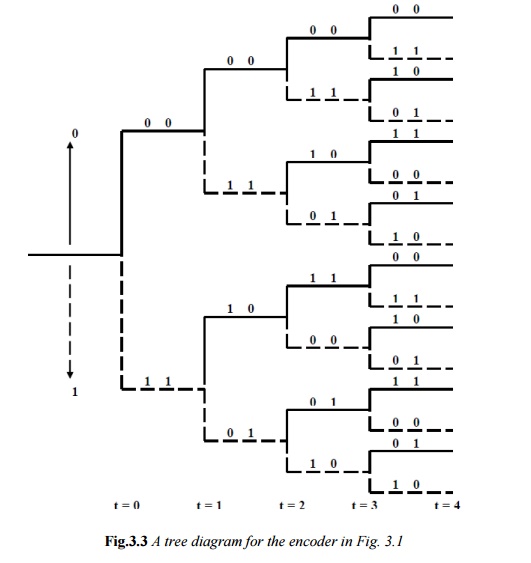
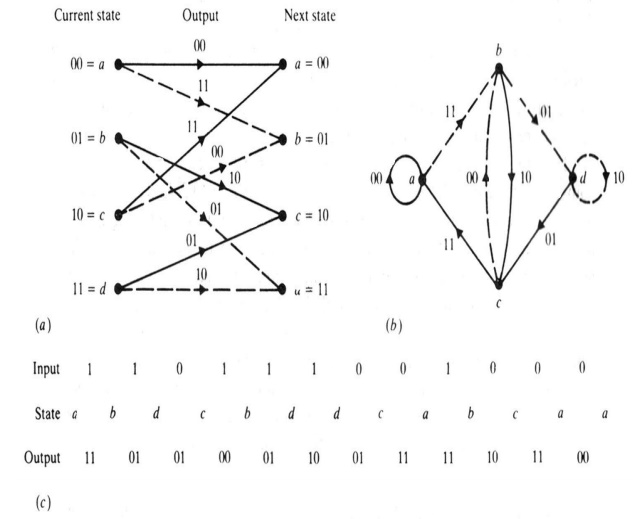
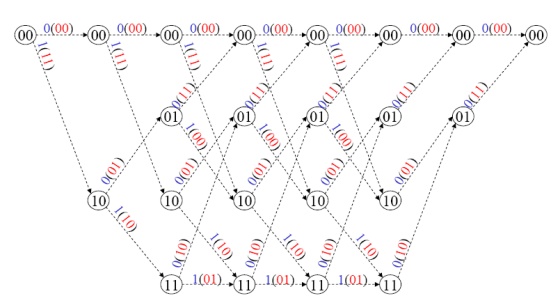
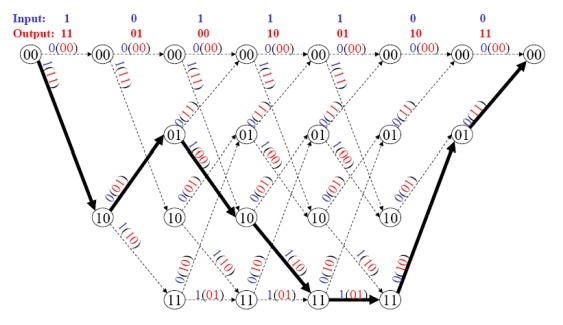
c) Trellis Diagram Representation:
The trellis diagram of a convolutional code is obtainedfrom its state diagram. All state transitions at each time step are explicitly shown in the diagram to retain the time dimension, as is present in the corresponding tree diagram. Usually, supporting descriptions on state transitions, corresponding input and output bits etc. are labeled in the trellis diagram. It is interesting to note that the trellis diagram, which describes the operation of the encoder, is very convenient for describing the behavior of the corresponding decoder, especially when the famous „Viterbi Algorithm (VA)‟ is followed. Fig. 3.4 shows the trellis diagram for the encoder in Figure 3.1.
Hamming Code Example:
H (7,4)
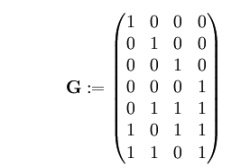
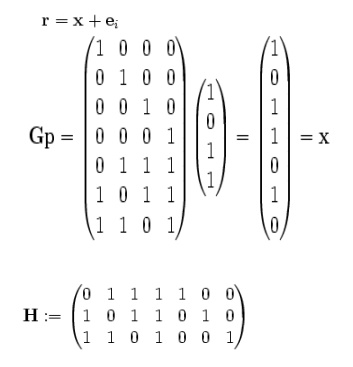
Generator matrix G: first 4-by-4 identical matrix
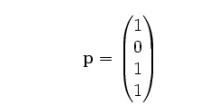
·Message information vector p
·Transmission vector x
·Received vector r and error vector e
· Parity check matrix H
Error Correction:
If there is no error, syndrome vector z=zeros
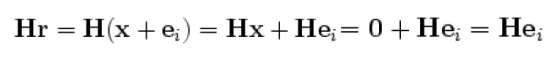
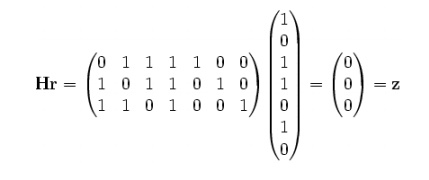
If there is one error at location 2
New syndrome vector z is
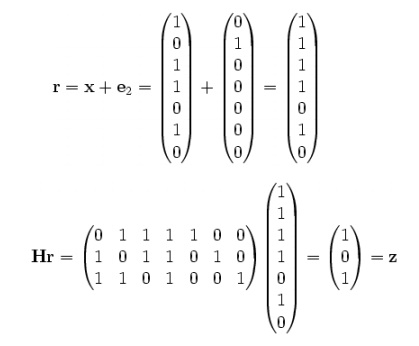
1. Consider a single error correction (7,4) linear code and the corresponding decoding table.
2. Find the (7,4) linear systematic block code word corresponding to 1101.Assume a suitable generator matrix.

n=7 k=4 q = n-k= 3
code vector G=[Ik: P]
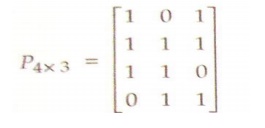
Check matrix C=MP
C1 = m1+m2+m3
C2= m2+m3+m4
C3= m1+m2+m4
C=[010]
Complete code word can be calculated X={M:C}={1 1 0 0 0 1 0}
The parity matrix H=[pT :I] =[I: pT] =

Minimum weight W(X)=3
3. Determine the generator polynomial g(X) FOR A (7,4) cyclic code and fine the code vector for the following data vector 1010, 1111 and 1000
n=7 k=4
q=n-k=3
To obtain the generator polynomial (p7+1) =(p+1)(p3+p2+1)(p3+p+1) Let G(p)= (p3+p+1)
To obtain the generator matrix in systematic form

To determine the code vector
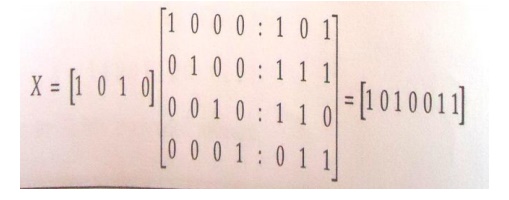
1. code vector for M=1010
X=MG
2. code vector for M=1111

4. Assume a (2,1) convolutional coder with constraint length 6.Draw the tree diagram, state diagram and trellis diagram for the assumed coder
Design block code for a message block of size eight that can correct for single errors Briefly discuss on various error control codes and explain in detail with one example for convolution code.
N=2, K=1 AND K=6 (CONSTRAIN LENGHT)
M=K/n=6/2=3, since constrain length k=n*M
3 storage element in shift register
N=2 two output bits
One set k=1 of shift register having 3 storage element the convolutional code structure is easy to draw from its parameters. First draw m boxes representing the m memory register. Then draw n modulo-2 adders to represent the n output bits. Now connect the memory registers to the adders using the generator polynomial
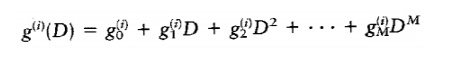
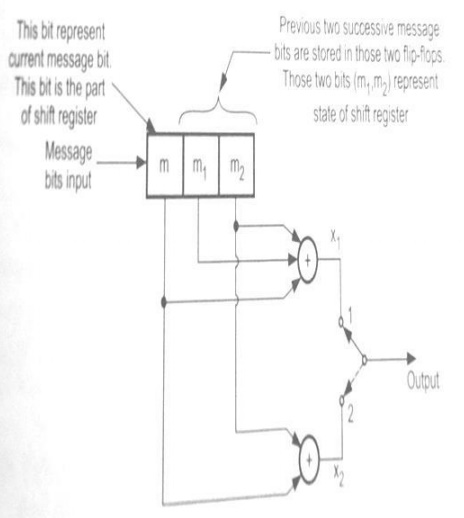
Convolutional codes
k = number of bits shifted into the encoder at one time
k=1 is usually used!!
n = number of encoder output bits corresponding to the k0020information bits
r = k/n = code rate
K = constraint length, encoder memory
Each encoded bit is a function of the present input bits and their past ones.
Generator Sequence
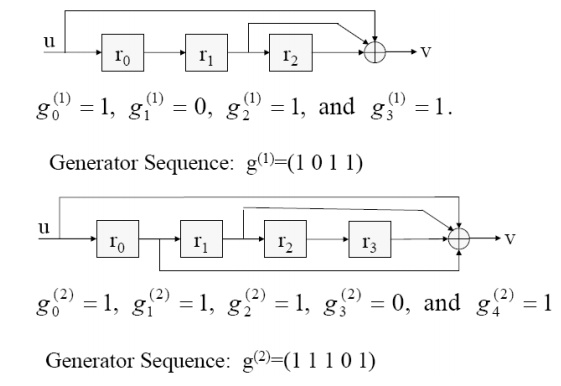
An Example – (rate=1/2 with K=2)

Related Topics