Intermediate Languages

INTERMEDIATE CODE GENERATION

INTRODUCTION

The front end translates a source program into an intermediate representation from which the back end generates target code.

Benefits of using a machine-independent intermediate form are:

1.         Retargeting is facilitated. That is, a compiler for a different machine can be created by attaching a back end for the new machine to an existing front end.

2.     A machine-independent code optimizer can be applied to the intermediate representation.

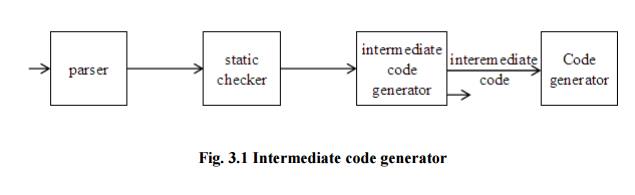
Fig. 3.1 Intermediate code generator

INTERMEDIATE LANGUAGES

Three ways of intermediate representation:

*    Syntax tree

*    Postfix notation

*    Three address code

The semantic rules for generating three-address code from common programming language constructs are similar to those for constructing syntax trees or for generating postfix notation.

Graphical Representations: Syntax tree:

A syntax tree depicts the natural hierarchical structure of a source program. A dag (Directed Acyclic Graph) gives the same information but in a more compact way because common subexpressions are identified. A syntax tree and dag for the assignment statement a : = b * - c + b * - c are shown in Fig.3.2:

Postfix notation:

Postfix notation is a linearized representation of a syntax tree; it is a list of the nodes of the tree in which a node appears immediately after its children. The postfix notation for the syntax tree given above is

Syntax-directed definition:

Syntax trees for assignment statements are produced by the syntax-directed definition. Non-terminal S generates an assignment statement. The two binary operators + and * are examples of the full operator set in a typical language. Operator associativities and precedences are the usual ones, even though they have not been put into the grammar. This definition constructs the tree from the input a : = b * - c + b* - c.

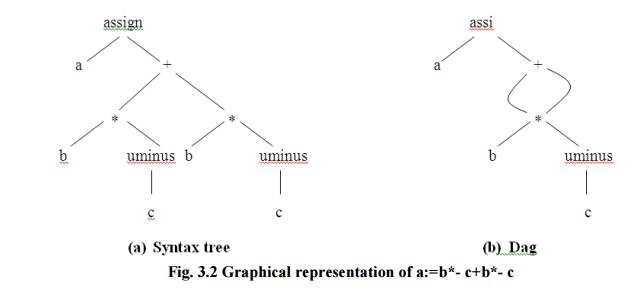
Fig. 3.2 Graphical representation of a:=b*- c+b*- c

Fig. 3.3 Syntax-directed definition to produce syntax

The token id has an attribute place that points to the symbol-table entry for the toen identifier. A symbol-table entry can be found from an attribute id.name, representing the lexeme associated with that occurrence of id. If the lexical analyzer holds all lexemes in a single array of characters, then attribute name might be the index of the first character of the lexeme.

Two representations of the syntax tree are as follows. In (a) each node is represented as a record with a field for its operator and additional fields for pointers to its children. In (b), nodes

are allocated from an array of records and the index or position of the node serves as the pointer to the node. All the nodes in the syntax tree can be visited by following pointers, starting from the root at position 10.

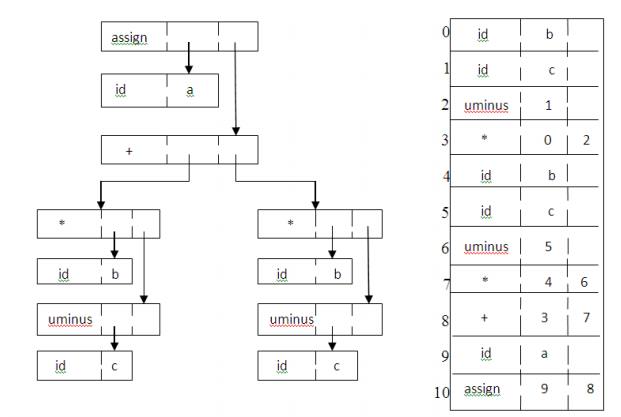
Fig. 3.4 Two representations of the syntax tree

Three-address code

Three-address code is a sequence of statements of the general form x : = y op z

where x, y and z are names, constants, or compiler-generated temporaries; op stands for any operator, such as a fixed- or floating-point arithmetic operator, or a logical operator on boolean-valued data. Thus a source language expression like x+ y*z might be translated into a sequence

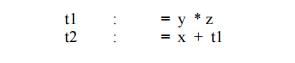
where t1 and t2 are compiler-generated temporary names.

Advantages of three-address code:

* The unraveling of complicated arithmetic expressions and of statements makes three-address code desirable for target code generation and optimization. * The use of names for the intermediate values computed by a program allows three-address code to be easily rearranged - unlike postfix notation.

Three-address code is a linearized representation of a syntax tree or a dag in which explicit names correspond to the interior nodes of the graph. The syntax tree and dag are represented by the three-address code sequences. Variable names can appear directly in three address statements.

Fig.3.5 Three-address code corresponding to the syntax tree and dag

The reason for the term “three-address code” is that each statement usually contains three addresses, two for the operands and one for the result.

Types of Three-Address Statements:

The common three-address statements are:

1.    Assignment statements of the form x : = y op z, where op is a binary arithmetic or logical operation.

2. Assignment instructions of the form x : = op y, where op is a unary operation. Essential unary operations include unary minus, logical negation, shift operators, and conversion operators that, for example, convert a fixed-point number to a floating-point number.

3. Copy statements of the form x : = y where the value of y is assigned to x.

4.     The unconditional jump goto L. The three-address statement with label L is the next to be executed.

5.  Conditional jumps such as if x relop y goto L. This instruction applies a relational operator (<, =, >=, etc. ) to x and y, and executes the statement with label L next if x stands in relation relop to y. If not, the three-address statement following if x relop y as in the usual sequence.

6. param x and call p, n for procedure calls and return y, where y representing a returned value is optional. For example,

7.Indexed assignments of the form x : = y[i] and x[i] : = y.

8.Address and pointer assignments of the form x : = &y , x : = *y, and *x : = y.

Syntax-Directed Translation into Three-Address Code:

When three-address code is generated, temporary names are made up for the interior nodes of a syntax tree. For example, id : = E consists of code to evaluate E into some temporary t, followed by the assignment id.place : = t.

Given input a : = b * - c + b * - c, the three-address code is as shown in Fig. 8.3a. The synthesized attribute S.code represents the three-address code for the assignment S.

The nonterminal E has two attributes :

1. E.place, the name that will hold the value of E , and

2. E.code, the sequence of three-address statements evaluating E.

Syntax-directed definition to produce three-address code for assignments

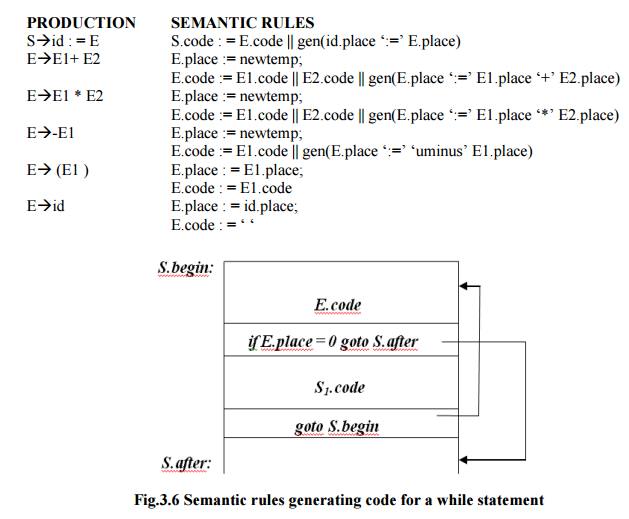
Fig.3.6 Semantic rules generating code for a while statement

PRODUCTION : SEMANTIC RULES

S->whileEdoS1: S.begin := newlabel;

S.after := newlabel;

S.code := gen(S.begin ‘:’) ||

E.code ||

gen ( ‘if’ E.place ‘=’ ‘0’ ‘goto’ S.after)|| S1.code ||

gen ( ‘goto’ S.begin) || gen ( S.after ‘:’)

The function newtemp returns a sequence of distinct names t1,t2,….. in response to successive calls.

Ø     Notation gen(x ‘:=’ y ‘+’ z) is used to represent three-address statement x := y + z. Expressions appearing instead of variables like x, y and z are evaluated when passed to gen, and quoted operators or operand, like ‘+’ are taken literally.

Ø     Flow-of-control statements can be added to the language of assignments. The code for S

while E do S1 is generated using new attributes S.begin and S.after to mark the first statement in the code for E and the statement following the code for S, respectively.

The function newlabel returns a new label every time it is called.

We assume that a non-zero expression represents true; that is when the value of E becomes zero, control leaves the while statement.

Implementation of Three-Address Statements:

A three-address statement is an abstract form of intermediate code. In a compiler, these statements can be implemented as records with fields for the operator and the operands. Three such representations are: Quadruples, Triples, Indirect triples

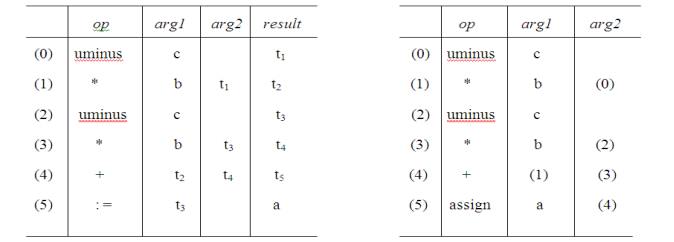
Fig.3.7 (a) Quadruples (b) Triples

Quadruples:

Ø     A quadruple is a record structure with four fields, which are, op, arg1, arg2 and result.

Ø     The op field contains an internal code for the operator. The three-address statement x : = y op z is represented by placing y in arg1, z in arg2 and x in result.

Ø     The contents of fields arg1, arg2 and result are normally pointers to the symbol- entries for the names represented by these fields. If so, temporary names must be entered into the symbol table as they are created.

Triples:

Ø     To avoid entering temporary names into the symbol table, we might refer to a temporary value by the position of the statement that computes it.

Ø     If we do so, three-address statements can be represented by records with only three fields: op, arg1 and arg2.

Ø     The fields arg1 and arg2, for the arguments of op, are either pointers to the symbol table or pointers into the triple structure ( for temporary values ).

Ø     Since three fields are used, this intermediate code format is known as triples.

A ternary operation like x[i] : = y requires two entries in the triple structure while x : = y[i] is naturally represented as two operations.

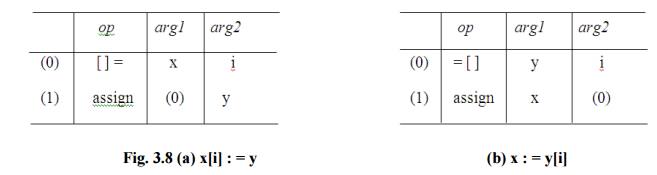
Fig. 3.8 (a) x[i] : = y (b) x : = y[i]

Indirect Triples:

Another implementation of three-address code is that of listing pointers to triples, rather than listing the triples themselves. This implementation is called indirect triples.

For example, let us use an array statement to list pointers to triples in the desired order. Then the triples shown above might be represented as follows:

Fig. 3.9 Indirect triples representation of three-address statements