Chapter: Principles of Compiler Design : Intermediate Code Generation
Assignment Statements
ASSIGNMENT STATEMENTS
Suppose that the context in which an
assignment appears is given by the following grammar.
P->M
D
M->ɛ
D->D ; D | id: T | proc id; N D ; S
N->ɛ
Nonterminal P becomes
the new start symbol when these productions are added to those in the tran
slation scheme shown below.
Translation scheme to produce three-address code for
assignments
S->id : = E { p : = lookup (
id.name); if p ≠ nil then
emit(
p ‘ : =’ E.place) else error }
E->E1 + E2 { E.place : = newtemp;
emit(
E.place ‘: =’ E1.place ‘ + ‘ E2.place ) }
E->E1 * E2 { E.place : = newtemp;
emit(
E.place ‘: =’ E1.place ‘ * ‘ E2.place ) }
E->-E1 { E.place : = newtemp;
emit
( E.place ‘: =’ ‘uminus’ E1.place ) }
E-> ( E1) { E.place : = E1.place }
E->id { p : = lookup ( id.name); if p
≠ nil then
E.place
: = p else error }
Reusing Temporary Names
The temporaries used to
hold intermediate values in expression calculations tend to clutter up the
symbol table, and space has to be allocated to hold their values. Temporaries
can be reused by changing newtemp. The code generated by the rules for E E1 +
E2 has the general form:
evaluate E1 into t1
evaluate E2 into t2
t : = t1 + t2
* The
lifetimes of these temporaries are nested like matching pairs of balanced
parentheses.
* Keep
a count c , initialized to zero. Whenever a temporary name is used as an
operand, decrement c by 1. Whenever a new temporary name is generated, use $c
and increase c by 1.
* For
example, consider the assignment x := a * b + c * d - e * f
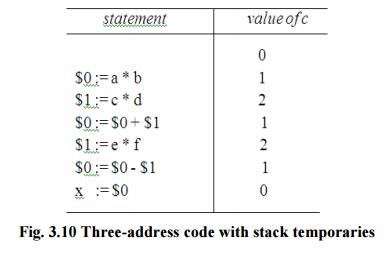
Fig.
3.10 Three-address code with stack temporaries
Addressing Array Elements:
Elements of an array
can be accessed quickly if the elements are stored in a block of consecutive
locations. If the width of each array element is w, then the ith element of
array A begins in location
base
+ ( i - low ) x w
where low is the lower
bound on the subscript and base is the relative address of the storage
allocated for the array. That is, base is the relative address of A[low].
The expression can be partially
evaluated at compile time if it is rewritten
ixw+ (base-low x w)
The subexpression c =
base - low x w can be evaluated when the declaration of the array is seen. We
assume that c is saved in the symbol table entry for A , so the relative
address of A[i] is obtained by simply adding i x w to c.
Address calculation of multi-dimensional
arrays:
A two-dimensional array is stored in of
the two forms :
Row-major (row-by-row)
Column-major
(column-by-column)
In the case of row-major form, the
relative address of A[ i1 , i2] can be calculated by the formula base + ((i1 -
low1) x n2 + i2 - low2) x w
where, low1 and low2
are the lower bounds on the values of i1 and i2 and n2 is the number of values
that i2 can take. That is, if high2 is the upper bound on the value of i2, then
n2 = high2 - low2 + 1.
Assuming that i1 and i2
are the only values that are known at compile time, we can rewrite the above
expression as
(( i1 x n2 ) + i2 ) x w + ( base - (( low1 x n2 ) +
low2 ) x w)

(a)
ROW-MAJOR (b) COLUMN-MAJOR
Fig.
3.11 Layouts for a 2 x 3 array
Generalized formula:
The expression
generalizes to the following expression for the relative address of A[i1,i2,…,ik]
(( . . . (( i1n2 + i2 ) n3 + i3) . . . ) nk + ik ) x w + base - (( . .
.((low1n2 + low2)n3 + low3) . . .) nk + lowk) x w
for all j, nj = highj - lowj + 1
The Translation Scheme for Addressing
Array Elements :
Semantic actions will be added to the grammar :
(1)
S-> L : = E
(2)
E-> E + E
(3)
E-> (E)
(4)
E-> L
(5)
L-> Elist ]
(6)
L-> id
(7)
Elist-> Elist , E
(8)
Elist-> id [ E
We generate a normal
assignment if L is a simple name, and an indexed assignment into the location
denoted by L otherwise :

When an array reference
L is reduced to E , we want the r-value of L. Therefore we use indexing to
obtain the contents of the location L.place [ L.offset ] :
(4) E-> L { if L.offset = null then
/* L is a simple id* / E.place : = L.place
else
begin
E.place
: = newtemp;
emit
( E.place ‘: =’ L.place ‘ [‘ L.offset ‘]’) end }
(5) L-> Elist ] { L.place
: = newtemp;
L.offset : = newtemp;
emit (L.place ‘: =’ c( Elist.array ));
(6) L-> id emit (L.offset ‘: =’ Elist.place ‘*’ width (Elist.array)) }
{ L.place := id.place;
L.offset := null }
(7) Elist-> Elist1 , E { t
:= newtemp;
m : = Elist1.ndim + 1;
emit ( t ‘: =’ Elist1.place ‘*’ limit (Elist1.array,m));
emit ( t ‘: =’ t ‘+’ E.place);
Elist.array : = Elist1.array;
Elist.place : = t;
(8) Elist-> id [ E Elist.ndim
: = m }
{ Elist.array : = id.place;
Elist.place : = E.place;
Elist.ndim : = 1 }
Type conversion within Assignments :
Consider the grammar
for assignment statements as above, but suppose there are two types - real and
integer , with integers converted to reals when necessary. We have another
attribute E.type, whose value is either real or integer. The semantic rule for
E.type associated with the production

The entire semantic rule for E = E+E ans most o the
other productions must modified to generate, when necessary, three-address
statements of the form x : = inttoreal y, whose effect is to convert integer y
to a real of equal value, called x.
Semantic action for
E-> E1+E2
E.place := newtemp;
if E1.type = integer and E2.type =
integer then begin emit( E.place ‘: =’ E1.place ‘int +’ E2.place);
E.type
: = integer
end
else if E1.type = real and E2.type = real then begin
emit(
E.place ‘: =’ E1.place ‘real +’ E2.place);
E.type
: = real
end
else if E1.type = integer and E2.type = real then
begin
u
: = newtemp;
emit( u ‘: =’ ‘inttoreal’ E1.place);
emit( E.place ‘: =’ u ‘
real +’ E2.place); E.type : = real end
else if E1.type = real and E2.type =integer then
begin
u
: = newtemp;
emit( u ‘: =’ ‘inttoreal’ E2.place);
emit( E.place ‘: =’
E1.place ‘ real +’ u); E.type : = real end
else
E.type : = type_error;
For example, for the input x : = y + i * j
assuming x and y have type real, and i
and j have type integer, the output would look like
t1 : = i int* j
t3
: = inttoreal t1
t2 : = y real+ t3
x : = t2
Related Topics