Interest rate Formulas

Interest Formulas

Interest Formulas 

Interest rate can be classified into simple interest rate and compound interest rate.

ü  In simple interest, the interest is calculated, based on the initial deposit for every interest period. In this case, calculation of interest on interest is not applicable.

ü  In compound interest, the interest for the current period is computed based on the amount (principal plus interest up to the end of the previous period) at the beginning of the current period.

The notations which are used in various interest formulae are as follows: P = principal amount

n =  No. of interest periods

i = interest rate (It may be compounded monthly, quarterly, semiannually or annually)

F =  future amount at the end of year n

A =  equal  amount deposited at the end of every interest period

G = uniform amount which will be added/subtracted period after period to/from the amount of deposit A1 at the end of period 1

Time Value of Money - . It represents the growth of capital per unit period. The period may be a month, a quarter, semiannual or a year.

An interest rate 15% compounded annually means that for every hundred rupees invested now, an amount of Rs. 15 will be added to the account at the end of the first year. So, the total amount at the end of the first year will be Rs. 115.

At the end of the second year, again 15% of Rs. 115, i.e. Rs. 17.25 will be added to the account.

Hence the total amount at the end of the second year will be Rs. 132.25. The process will continue thus till the specified number of years.

If an investor invests a sum of Rs. 100 in a fixed deposit for five years with an interest rate of 15% compounded annually, the accumulated amount at the end of every year will be as shown in Table

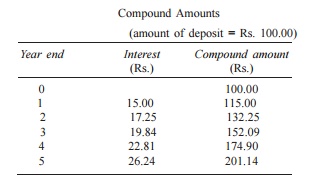
                   Compound Amounts

                   (amount of deposit = Rs. 100.00)

          Year end    Interest       Compound amount

                   (Rs.)  (Rs.)

          0                 100.00       

          1        15.00 115.00       

          2        17.25 132.25       

          3        19.84 152.09       

          4        22.81 174.90       

          5        26.24 201.14       

The formula to find the future worth in the third column is

F = P    (1 + i)ⁿ

where

P = principal amount invested at time 0, F = future amount,

i = interest rate compounded annually, n = period of deposit.

The maturity value at the end of the fifth year is Rs. 201.14. This means that the amount Rs. 201.14 at the end of the fifth year is equivalent to Rs. 100.00 at time 0 (i.e. at present). This is diagrammatically shown in Fig. 3.1. This explanation assumes that the inflation is at zero percentage.

Single-Payment Compound Amount - Here, the objective is to find the single future sum (F) of the initial payment (P) made at time 0 after n periods at an interest rate i compounded every

Cash flow diagram of single-payment compound amount.

The formula to obtain the single-payment compound amount is

F = P(1 + i)ⁿ = P(F/P, i, n)

where

(F/P, i, n) is called as single-payment compound amount factor.

Single-Payment Present Worth Amount - Here, the objective is to find the present worth amount (P) of a single future sum (F) which will be received after n periods at an interest rate of i compounded at the end of every interest period.

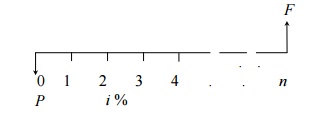
Cash flow diagram of single-payment present worth amount.

The formula to obtain the present worth is

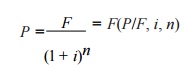
Where

(P/F, i, n) is termed as single-payment present worth factor.

Equal-Payment Series Sinking Fund

In this type of investment mode, the objective is to find the equivalent amount (A) that should be deposited at the end of every interest period for n interest periods to realize a future sum (F) at the end of the nth interest period at an interest rate of i.

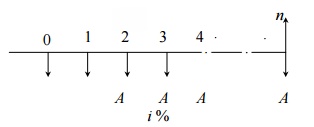
A = equal amount to be deposited at the end of each interest period n = No. of interest periods

i = rate of interest

F = single future amount at the end of the nth period

The formula to get F is

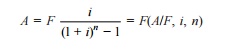
Where

(A/F, i, n) is called as equal-payment series sinking fund factor.

Equal-Payment Series Present Worth Amount The objective of this mode of investment is to find the present worth of an equal payment made at the end of every interest period for n interest periods at an interest rate of i compounded at the end of every interest period.

The corresponding cash flow diagram is shown in Fig. 3.8. Here,

P = present worth

A = annual equivalent payment i = interest rate

n = No. of interest periods

The formula to compute P is

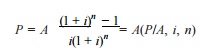
Where

(P/A, i, n) is called equal-payment series present worth factor

 Equal-Payment Series capital recovery The objective of  this  mode  of  investment  is to  find  the  annual equivalent amount (A) which is to be recovered at the end of every interest period for n interest periods for a loan (P) which is sanctioned now at an interest

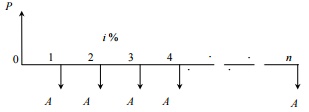
Cash flow diagram of equal-payment series capital recovery amount.

P = present worth (loan amount)

A = annual equivalent payment (recovery amount) i = interest rate

n = No. of interest periods

The formula to compute P is as follows:

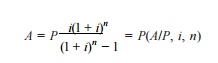
Where,

(A/P, i, n) is called equal-payment series capital recovery factor.

Uniform Gradient series annual equivalent The objective of this mode of investment is to find the annual equivalent amount of a series with an amount A1 at the end of the first year and with an equal increment (G) at the end of each of the following n – 1 years with an interest rate i compounded annually.

The corresponding cash flow diagram is shown in Fig

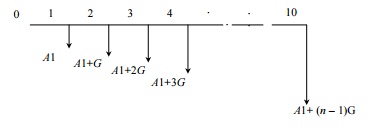
Cash flow diagram of uniform gradient series annual equivalent amount.

The formula to compute A under this situation is

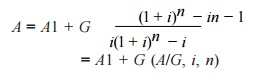
here Where

(A/G, i, n) is called uniform gradient series factor

Effective Interest rate Let i be the nominal interest rate compounded annually. But, in practice, the compounding may occur less than a year. For example, compounding may be monthly, quarterly, or semi-annually. Compounding monthly means that the interest is computed at the end of every month. There are 12 interest periods in a year if the interest is compounded monthly. Under such situations, the formula to compute the

effective interest rate, which is compounded annually, is Effective interest rate, 

R = 1 + i/C ^C − 1

where,

i = the nominal interest rate

C = the number of interest periods in a year.