Definition, Formula, Solved Example Problems, Exercise | Mathematics - Infinite Sequences and Series | 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
Chapter: 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
Infinite Sequences and Series
Infinite Sequences and Series
A finite sum of real numbers is well defined by the properties of real numbers, but in order to make sense of an infinite series, we need to consider the concept of convergence. Consider the infinite sum: ½ + ¼ + 1/8 + · · · with each term positive. Can we assign a numerical value to the sum? While at first it may seem difficult or impossible, we can certainly do something similar where we have one quantity getting closer and closer to a fixed quantity.
Let us discuss an interesting problem. Let there be two plates A and B. Let a full cake be placed on the plate A and let B as empty. Let us cut the cake in A into exactly two equal parts and place one part on B leaving the other part in A. Let us cut the remaining part of the cake in A into exactly two equal parts and place one part on B leaving the other part in A. Let us again cut the remaining part of the cake in A into exactly two equal parts and place one part on B leaving the other part in A. If we go on doing this what will happen? What will be the amount of cake “finally” in A and in B? Let us list the stage by stage status:
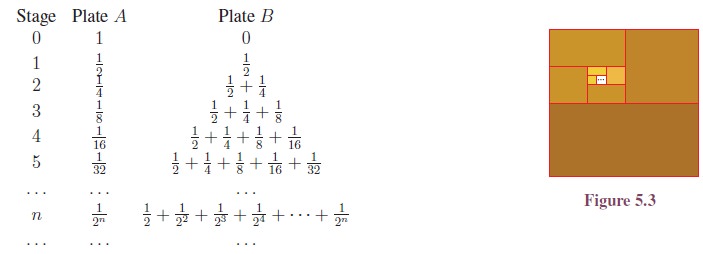
Intuitively we feel that “finally” nothing will remain in plate A and the full cake will be in plate B. In other words, the cake available in A is 0 and the cake available in B is 1. That is, intuitively we feel that


goes to some number. In other words, this sequence do not converge to any limit. So a sequence may not have a limit. But we can prove that a sequence cannot converge to more than one limit; that is, if a sequence converges to a limit, then it is unique.
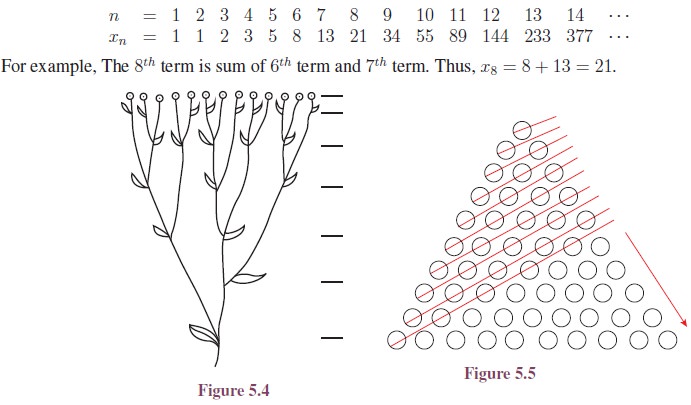
1. Fibonacci Sequence
The Fibonacci sequence is a sequence of numbers where a number other than first two terms, is found by adding up the two numbers before it. Starting with 1, the sequence goes 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth. Written as a rule, the expression is xn = xn−1 + xn−2, n ≥ 3 with x0 = 1, x1 = 1
Named after Fibonacci, also known as Leonardo of Pisa or Leonardo Pisano, Fibonacci numbers were first introduced in his Liber abaci in 1202. The son of a Pisan merchant, Fibonacci traveled widely and traded extensively. Mathematics was incredibly important to those in the trading industry, and his passion for numbers was cultivated in his youth.
Knowledge of numbers is said to have first originated in the Hindu-Arabic arithmetic system, which Fibonacci studied while growing up in North Africa. Prior to the publication of Liber abaci, the Latin-speaking world had yet to be introduced to the decimal number system. He wrote many books about geometry, commercial arithmetic and irrational numbers. He also helped in the development of the concept of zero.

Infinite Series



The problem of finding the values of x for which sequences of this form converges is beyond the scope of this book. However in the rest of the chapter we list some series with the appropriate values of x for which the series converges and the sum of the series whenever it converges.
2. Infinite Geometric Series


3. Infinite Arithmetico-Geometric Series
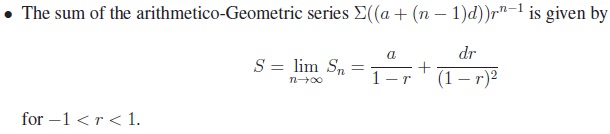

4. Telescopic Summation for Infinite Series
We discussed about summing terms of a finite sequence using telescopic summation technique in Section 5.5.2. The same applies for infinite series also.

5. Binomial Series
In the discussion on geometric series we have seen that
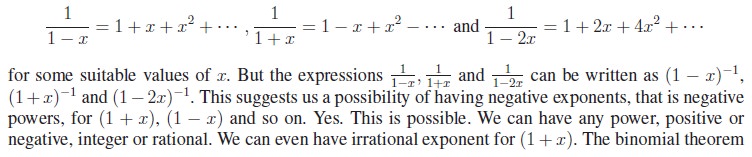
(Theorem 5.1) we proved already is for positive integral exponent (integral exponent means integer power). Now let us state the binomial theorem for rational power.
Binomial Theorem for Rational Exponent
Theorem 5.4 (Binomial Theorem for Rational Exponent): For any rational number n,
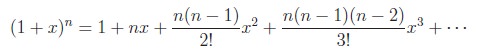
for all real numbers x satisfying |x| < 1.
As the proof involves higher mathematical concepts, let us assume the theorem without proof and see some particular cases and solve some problems. In the theorem
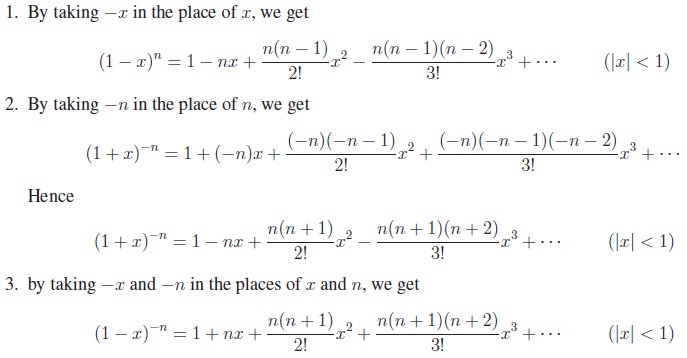
Even though we have explicitly mentioned that n is a rational number in the theorem, some of us may hesitate to use n in place of a general rational number. So we give the theorem using the representation p/q for a rational number.
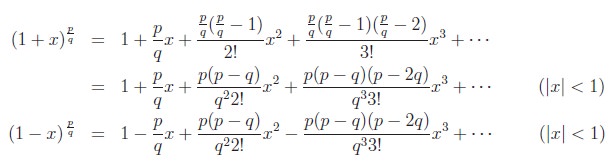
Though the theorem gives a formula to compute (1 + x)n, to solve numerical problems quickly we must remember and able to write certain expansions directly. Observation of the coefficient in each of such expansions will be very helpful in solving problems. Let us list some of them: (Try yourself!).
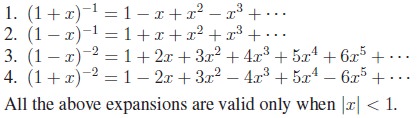



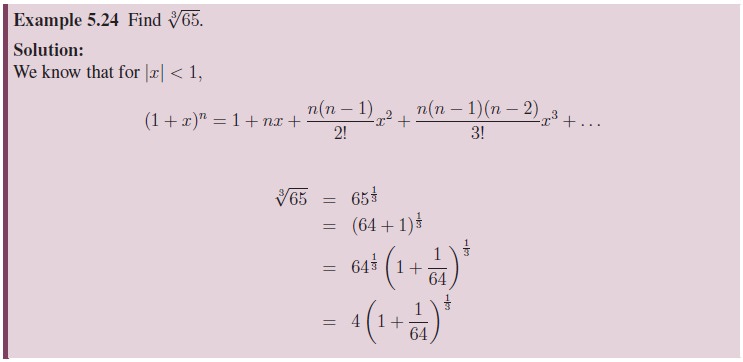


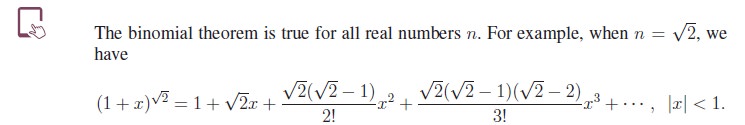
6. Exponential Series


7. Logarithmic Series
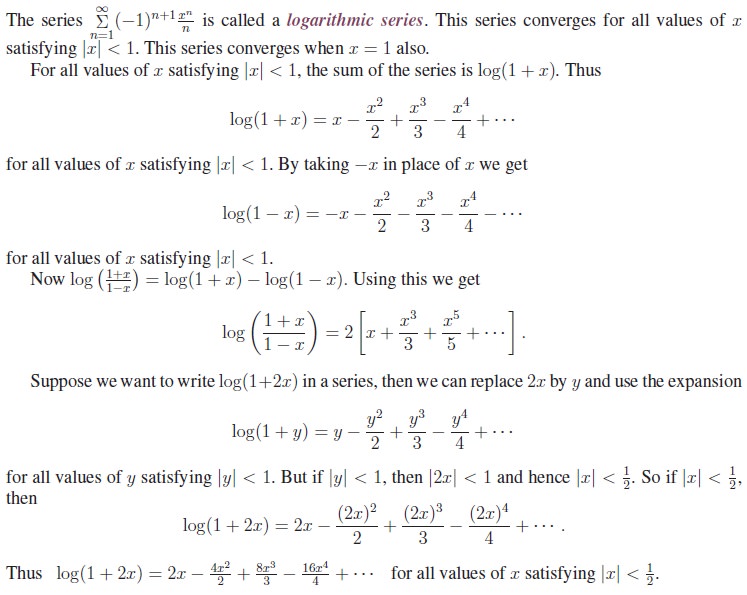

Related Topics