Finite Sequences

Finite Sequences

A sequence is a list of elements with a particular order. While the idea of a sequence of numbers, a₁, a₂, · · · , is straight forward, it is useful to think of a sequence as a function whose domain is either the set of first n natural numbers or N. Throughout this chapter, we consider only sequences of real numbers and we will refer to them as sequences. The arithmetic sequences and geometric sequences are also known as arithmetic progressions(AP) and geometric progressions (GP). Let us recall, the basic definitions of sequences and series.

·        If X is any set and n ∈ N, then any function f : {1, 2, 3, . . . , n} → X is called a finite sequence on X and any function g : N → X is called an infinite sequence on X. The value f(n) of the function f at n is denoted by a_n and the sequence itself is denoted by (a_n).

·        If the set X happens to be a set of real numbers, the sequence is called a numerical sequence or a sequence of real numbers.

·        Though every sequence is a function, a function is not necessarily a sequence.

·        Unlike sets, where elements are not repeated, the terms in a sequence may be repeated. In particular, a sequence in which all terms are same is called a constant sequence.

·        A useful way to visualise a sequence (a_n) is to plot the graph of {(n, a_n) : n ∈ N} which gives some details about the sequence.

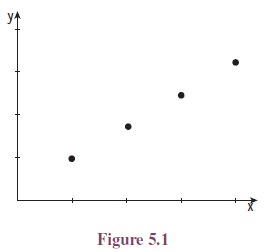
1. Arithmetic and Geometric Progressions

Progressions are some special cases of sequences where the terms of the sequences are either in increasing form or decreasing form.

We recall some definitions and results we discussed in earlier classes on arithmetic and geometric progressions.

Arithmetic Progression (AP)

Geometric Progression (GP)

It is interesting to note that the constant sequence c, c, c, . . . is an arithmetic sequence and is also a geometric sequence if c ¹ 0.

Let us consider the special constant sequence 0, 0, 0, 0, . . . . We have no problem in seeing this as an arithmetic sequence. But when we try to see this as a geometric sequence clearly the initial term a must be 0. What can we say about the common ratio r? If we take r as 1, 2 or any other number we get the same sequence 0, 0, 0, 0, . . . . We are left with the situation where a geometric sequence has infinitely many common ratios. To overcome these confusions some mathematicians exclude this sequence from the class of geometric sequences by assuming a = 0 in the definition. (We made this assumption)

2. Arithmetico-Geometric Progression (AGP)

Combining arithmetic and geometric progressions, a new progression called arithmetico geometric progression is formed. As we use the abbreviations AP and GP for arithmetic progressions and geometric progressions, we use the abbreviation AGP for arithmetico geometric progression. AGP’s arise in various applications, such as the computation of expected value in probability theory.

3. Harmonic Progression (HP)

Harmonic progression is one of many important sequences and is closely related to the arithmetic progression. Harmonic progression is widely used.

Note that a sequence is in harmonic progression if its reciprocals are in arithmetic progression. But we should not say that harmonic progressions are reciprocals of arithmetic progressions; in fact, if an arithmetic sequence contains a zero term, then its reciprocal is not meaningful. Of course, if an arithmetic progression contains no zero term, then its reciprocal is a harmonic progression. So a general harmonic progression will be of the form

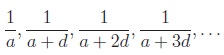
As the denominator of a fraction cannot be 0, a + kd ¹ 0 for any integer k ≥ 0. So the condition ^–a/a is not a whole number is essential. Problems in harmonic progression can be converted into problems in arithmetic progression and be solved using arithmetic progression techniques and formulae.

What can we say about constant sequences? All constant sequences other than the zero sequence are harmonic progressions also.

4. Arithmetic, Geometric and Harmonic Mean

We know the concept of “average”. There are many “averages”. Arithmetic mean (AM), Geometric mean(GM) and Harmonic mean(HM) are also some averages. Let us now recall the definitions of arithmetic mean and geometric mean, where the terms need not in AP or GP.

Arithmetic Mean and Geometric Mean

The numbers a₁, a₂, a₃, . . . , a_n need not be distinct and it is not necessary that the numbers are positive. It easily follows from the definition that 16 is the arithmetic mean of the numbers 14, 14, 17, 20, 15.

Taking the multiplication in place of addition and n^th root in place of division by n in the definition of arithmetic mean we get the definition of geometric mean.

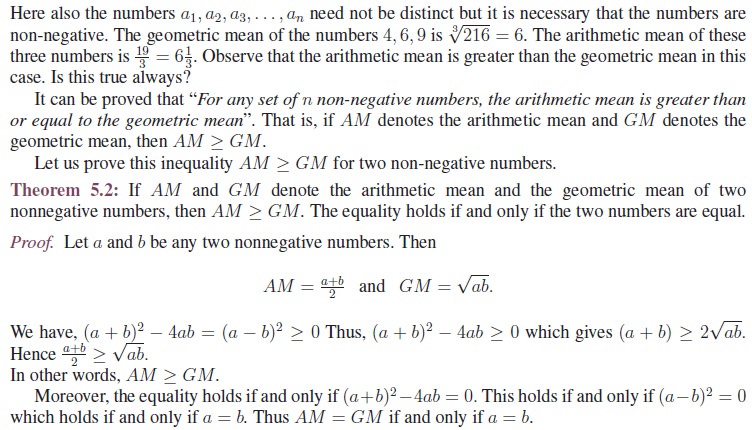
Geometrical Proof for AM ≥ GM

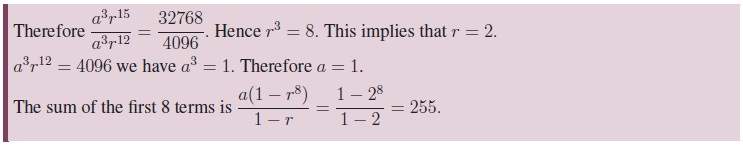
Harmonic Mean

It can be proved that “For any set of n positive numbers, the geometric mean is greater than or equal to the harmonic mean”. That is, GM ≥ HM.

Let us prove this inequality GM ≥ HM for two non-negative numbers.

Theorem 5.3: If GM and HM denote the geometric mean and the harmonic mean of two non-negative numbers, then GM ≥ HM. The equality holds if and only if the two numbers are equal.

Proof. Let a and b be any two positive numbers. Then

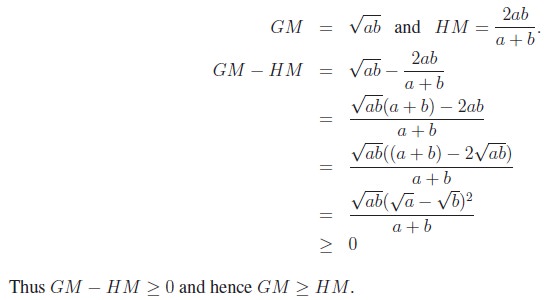
We have already proved that AM ≥ GM and now we have GM ≥ HM. Combining these two, we have an important inequality AM ≥ GM ≥ HM.

Result 5.3: For any two positive numbers, the three means AM, GM and HM are in geometric progression.