Important Short Questions and Answers: Analysis of Discrete Time Signals

1. What is the relation between Z transform and fourier transform of discrete time  signal.

 X(ω)=X(Z)|z=e^jω.This means Z transform is same as fourier transform when

 evaluated on unit circle.

2. Define region of convergence with respect to Z transform.

 Region of convergence (ROC) is the area in Z plane where Z transform convergence

 .In other word, it is possible to calculate the X(z) in ROC.

3. State the initial value theorem of Z transforms.

 The initial value of the sequence is given as, X(0)=lim_z->1X(z).

4. What is meant by aliasing?

 When the high frequency interferes with low frequency and appears as low

 then the phenomenon is called aliasing.

5. Define Nyquist rate and Nyquist interval.

When the sampling rate becomes exactly equal to ‘2W’ samples/sec,for a give bandwidth of W hertz, then it is called Nyquist rate .’

Nyquist interval is the time interval between any two adjacent samples.

Nyquist rate =2W hz&Nyquist interval=1/2W seconds.

6. Define unilateral Z-Transform or one sided Z-transform

The unilateral Z-Transform of signal x(t) is given as,

The unilateral and bilateral Z-Transforms are same for causal signals.

7. State the final value theorem for z-transform.

The final value of a sequence is given as,

8. Define DTFT pair.

DTFT,

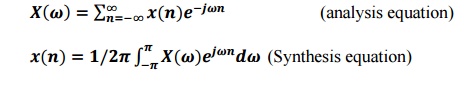
9. State the sampling theorem.

• A bandwidth signal of finite energy, which has no frequency components higher than W hertz, is completely described by specifying the values of the signal at instants of time separated by 1/2W seconds.

• A band limited signal of finite energy, which has no frequency components higher than W hertz, may be completely recovered from the knowledge of its samples taken at the rate of 2W samples per second.

10. Define two sided Z transform.

The z- transform of the DT signal is given by,

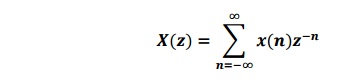
Here ‘z’ is the complex variable. The z- transform pair is denoted by,

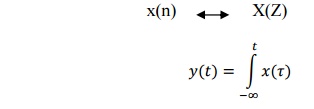
11. State the convolution property of z transform.

The convolution states that,

That is the convolution of two sequences in time domain is equivalent to multiplication of their z-transforms.

12. State parseval‟s theorem.

Consider the complex valued sequences x(n) and y(n).

If x(n)----_X(k)

y(n)----_Y(k)

then x(n)y*(n)=1/N X(k)Y*(k)

13. Find Z transform of x(n)={1,2,3,4} x(n)= {1,2,3,4}

X(z)= x(n)z-n

= 1+2z-1+3z-2+4z-3.

= 1+2/z+3/z2+4/z3.

14. What z transform of (n-m)?

By time shifting property

Z[A (n-m)]=AZ-m sinZ[ (n)] =1

15. Obtain the inverse z transform of X(z)=1/z-a,|z|>|a|

Given X(z)=z-1/1-az-1

By time shifting property

X(n)=an.u(n-1)