Chapter: Signals and Systems : Analysis of Discrete Time Signals
Analysis of Discrete Time Signals
ANALYSIS OF DISCRETE TIME SIGNALS
Sampling theory
Let x(t)
be a continuous signal which is to be sampled, and that sampling is performed
by measuring the value of the continuous signal every T seconds, which is called the sampling interval. Thus, the sampled
signal x[n] given by:x[n]
= x(nT), with n = 0, 1, 2, 3,
...
The
sampling frequency or sampling rate fs
is defined as the number of samples obtained in one second, or fs = 1/T. The sampling rate is measured in hertz or in samples per second.
The
frequency equal to one-half of the sampling rate is therefore a bound on the
highest frequency that can be unambiguously represented by the sampled signal.
This frequency (half the sampling rate) is called the Nyquist frequency of the
sampling system. Frequencies above the Nyquist frequency fN can be observed in the sampled signal, but their frequency is
ambiguous. That is, a frequency component with frequency f cannot be distinguished from other components with frequencies NfN + f and NfN – f for nonzero integers N. This ambiguity is called aliasing. To
handle this problem as gracefully as possible, most analog signals are filtered
with an anti-aliasing filter (usually a low-pass filter with cutoff near the
Nyquist frequency) before conversion to the sampled discrete representation.
The
theory of taking discrete sample values (grid
of color pixels) from functions defined over continuous domains (incident radiance defined over the film
plane) and then using those samples to reconstruct new functions that are
similar to the original (reconstruction).
Sampler: selects sample points on the
image plane
Filter: blends multiple samples
together
Sampling Theorem:
Sampling
Theorem: bandlimited signal can be reconstructed exactly if it is sampled at a
rate atleast twice the maximum frequency component in it."
Consider
a signal g(t) that is bandlimited.
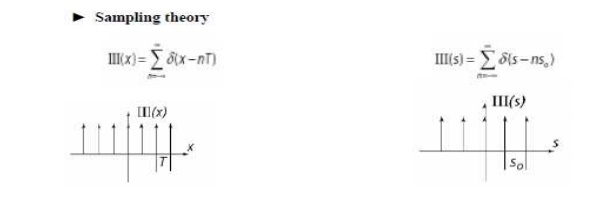
The
maximum frequency component of g(t) is fm. To recover the signal g(t) exactly
from its samples it has to be sampled ata rate fs _ 2fm. The minimum
required sampling rate fs = 2fm is called nyquist rate
A
continuous time signal can be processed by processing its samples through a
discrete time system. For reconstructing the continuous time signal from its
discrete time samples without any error, the signal should be sampled at a
sufficient rate that is determined by the sampling theorem.
Aliasing
Aliasing
is a phenomenon where the high frequency components of the sampled signal interfere
with each other because of inadequate sampling ωs< 2ωm. Aliasing
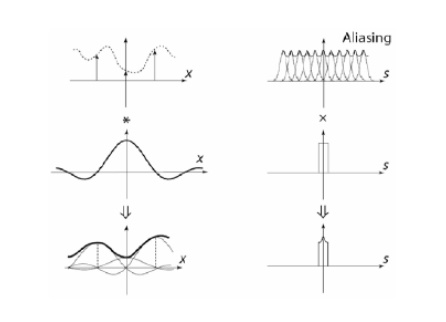
Aliasing
leads to distortion in recovered signal. This is the reason why sampling
frequency should be atleast twice the bandwidth of the signal.
Sampling of Non-bandlimited Signal:
Anti-aliasing Filter
Anti
aliasing filter is a filter which is used before a signal sampler, to restrict
the
bandwidth
of a signal to approximately satisfy the sampling theorem. The potential
defectors are all the frequency components beyond fs/2 Hz. We should have to eliminate these components
from x(t) before sampling x(t). As a result of this we lose only
the components beyond the folding frequency fs/2
Hz. These frequency components cannot reappear to corrupt the components with
frequencies below the folding frequency. This suppression of higher frequencies
can be accomplished by an ideal filter of bandwidth fs/2 Hz. This filter is called the anti-aliasing filter. The anti aliasing operation must be performed
before the signal is sampled. The anti aliasing filter, being an ideal filter
is unrealizable. In practice, we use a steep cutoff filter, which leaves a
sharply attenuated residual spectrum beyond the folding frequency fs/2.
DISCRETE TIME FOURIER TRANSFORM
In
mathematics, the discrete-time Fourier
transform (DTFT) is one of the specific
forms of
Fourier analysis. As such, it transforms one function into another, which is
called the frequency domain
representation, or simply the "DTFT", of the original function (which
is often a function in the time-domain). But the DTFT requires an input
function that is discrete. Such
inputs are often created by sampling a continuous function, like a
person's voice.



Inverse transform
The
following inverse transforms recover the discrete-time sequence:
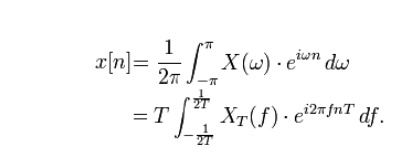
The
integrals span one full period of the DTFT, which means that the x[n] samples
are also the coefficients of a Fourier series expansion of the DTFT.
Infinite
limits of integration change the transform into a continuous-time Fourier
transform [inverse], which produces a sequence of Dirac impulses. That is:
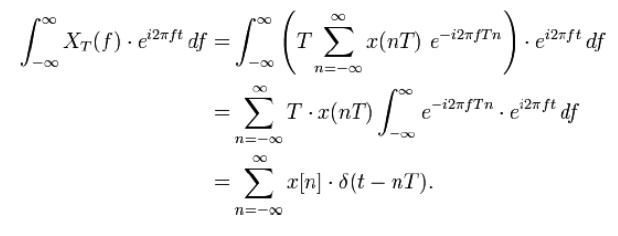
Properties


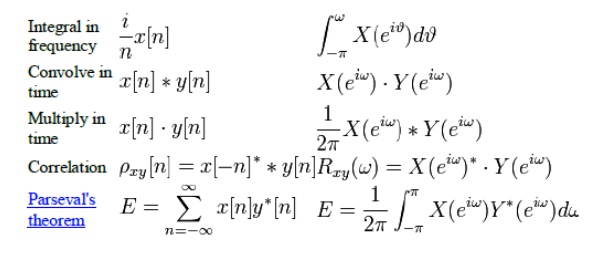
SYMMETRY PROPERTIES
The
Fourier Transform can be decomposed into a real and imaginary part or into an
even and odd part.


Z-transforms
Definition: The Z – transform of a discrete-time signal x(n)
is defined as the power series:

where z is a complex variable. The above given
relations are sometimes called the
direct Z-transform because they
transform the time-domain signal x(n)into
its complex-plane representation X(z).
Since Z – transform is an infinite
power series, it exists only for those values of z for which this series converges.
The region of convergence of X(z) is the set of all values of z for which X(z) attains a finite value.
For discrete-time systems, z-transforms play the same role of
Laplace transforms do in continuous-time systems


Using the
definition requires a contour integration in the complex z-plane.
Fortunately,
we tend to be interested in only a few basic signals (pulse, step, etc.)
Virtually all of the signals we’ll see can be built up from these basic
signals.
Z transform properties

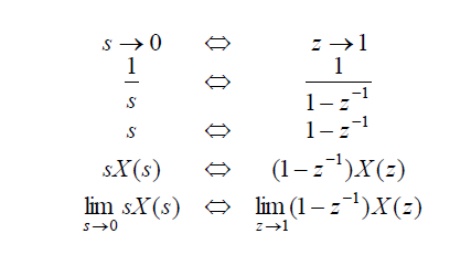





Related Topics