Important Short Objective Question and Answers: Solution of Equations and Eigenvalue Problems

1. What is the order of convergence of Newton-Raphson methods if the multiplicity of the root is one.

Sol:

Order of convergence of N.R method is 2

2.      Derive   Newton’s   algorithm root of number Nth.   for   finding   the

Sol:

If x= N ^1/p ,

Then x^p-N = 0 is the equation to be solved.

By N.R rule, if x_r is the r ^th iterate

3. What is the rate of convergence in N.R method?

Sol:

The rate of convergence in N.R method is of order 2

4. Define round off error.

Sol:

The round off error is the quantity R which must be added to the finite representation of a computed number in order to make it the true representation of that number.

5. State the principle used in Gauss-Jordan method.

Sol:

Coefficient matrix is transformed into diagonal matrix.

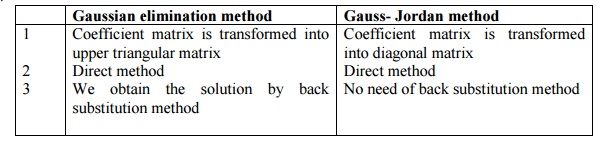
6. Compare Gaussian elimination method and Gauss- Jordan method.

Sol:

7. Determine the largest eigen value and the corresponding eigen value vector of the matrix correct to two decimal places using power method.

Sol:

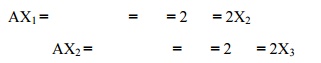
This shows that the largest eigen value = 2

The corresponding eigen value =

8. Write the Descartes rule of signs

Sol:

1) An equation f (x) = 0 cannot have more number of positive roots than there are changes of sign in the terms of the polynomial f (x) .

2)An equation f (x) = 0 cannot have more number of positive roots than there are changes of sign in the terms of the polynomial f (x) .

9. Write a sufficient condition for Gauss seidel method to converge .(or) State a sufficient condition for Gauss Jacobi method to converge.

Sol:

The process of iteration by Gauss seidel method will converge if in each equation of the system the absolute value of the largest coefficient is greater than the sum of the

absolute values of the remaining coefficients.

10. State the order of convergence and convergence condition for NR method?

Sol:

The order of convergence is 2 Condition of convergence is

11. Compare Gauss Seidel and Gauss elimination method?

Sol:

12) Is the iteration method a self correcting method always?

Sol:

In general iteration is a self correcting method since the round off error is smaller.

13) If g(x) is continuous in [a , b] then under what condition the iterative method x = g(x) has a unique solution in [a , b].

Sol:

Let x = r be a root of x = g(x) .Let I = [a , b] be the given interval combining the point x = r. if g′(x) for all x in I, the sequence of approximation x₀ , x ₁,......x _nwill converge to the root r, provided that the initial approximation x₀ is chosen in r.

14) When would we not use N-R method .

Sol:

If  x₁ is the exact root and  x₀ is its approximate value of the equation

f (x) = 0.we know that 

this, method will be a slow process or may even be impossible.

Hence the method should not be used in cases where the graph of the function when it crosses the x axis is nearly horizontal.

15) Write the iterative formula of NR method.

Sol:

X_n+1 = x_n