Chapter: Mechanical : Gas Dynamics and Jet Propulsion : Basic Concepts and Isentropic Flows
Important Questions and Answers: Isentropic Flows
GAS DYNAMICS AND JET PROPULSION
1.What is the basic difference between
compressible and incompressible fluid flow?
Compressible
1. Fluid velocities are appreciable
compared with the
velocity of sound
2. Density is not constant
3. Compressibility factor is greater than
one.
Incompressible
1. Fluidvelocitiesaresmall compared with
the velocity of sound
2. Density is constant
3. Compressibility factor is one.
2. Write the steady flow energy equation for an
adiabatic flow of air.
In an adiabatic flow q = 0. Therefore energy equation becomes.
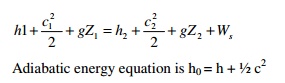
3. Define the mach number in terms of bulk modulus
of elasticity.
Mach number is a non-dimensional number and is
used for the analysis of compressible fluid flows.

4. Explain the meaning of stagnation state with
example.
The state
of a fluid attained by isentropically decelerating it to zero velocity at zero
elevation is referred as stagnation state.
(e.g.)
Fluid in a reservoir (or) in a settling chamber.
5. Distinguish between static and stagnation
pressures.
In
stagnation pressure state, the velocity of the flowing fluid is zero whereas in
the static pressure state, the fluid velocity is not equal to zero.
6. Differentiate between the static and stagnation
temperatures.
The actual temperature of the fluid in a
particular state is known as “static temperature” whereas the
temperature of the fluid when the fluid velocity is zero at zero elevation
is known as “stagnation temperature”.

7. What is the use of mach number?
Mach number is defined as the ratio between the local fluid velocity to the velocity of sound.
i.e. Mach number
M = Local
fluid velocity / Velocity of sound = c/ a
It is used for the analysis of compressible fluid
flow problems. Critical mach number is a dimensionless number at which the
fluid velocity is equal to its sound velocity. Therefore,
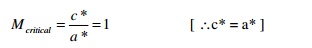
Crocco
number is a non – dimensional fluid velocity which is defined as the ratio of
fluid velocity to its maximum fluid velocity.

8. Write down the relationship between stagnation
and static temperature interms of the flow, mach number for the case of
isentropic flow.
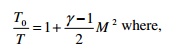
T0= stagnation temperature
T= Static temperature
M= Mach
number.
9.Give
the expression of p/P0 for an isentropic flow through a duct.
The
expression of
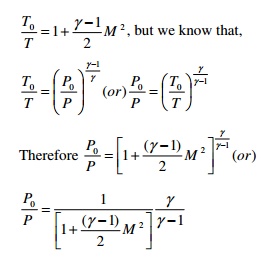
10. Name
the four reference velocities that are used in expressing the fluid velocities
in
non-dimensional
form?

11.
What are the different regions of
compressible flow.
![]()
The
adiabatic energy equation for a perfect gas is derived in terms of fluid
velocity © and sound velocity (a). This is then plotted graphically on the c- a
co-ordinates, a steady flow ellipse is obtained.
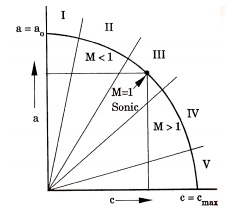
The
various regions of flow are:
i.Incompressible
region (M ≈ 0)
(ii) Subsonic region (M < 1)
(iii) Transonic region (0.8 – 1.2)
(iv) Supersonic region (M > 1 and M < 5)
(v) Hypersonic region (M ≥ 5)
12. Define
M* and give
the relation between
M
and M*.
It is a
non-dimensional mach number and is defined by the ratio between the local fluid
velocity to its critical velocity of sound / fluid.
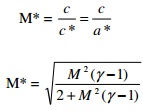
13. If
an aeroplane goes
to higher altitudes
maintaining the same
speed, the Mach
number
will remain constant. Say true or false.
False.
W.K.T. M
= c/a
At higher altitude, the sound velocity ‘a’ will
decrease and hence M will increase. Therefore, M is not constant.
14. Show
h – S
diagram for the
flow through a
nozzle. Show how
the stagnation
properties
get affected.
1 – 2’ =
Isentropic expansion
1 – 2 =
Adiabatic expansion
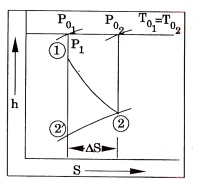
It is
assumed that, the exit pressure is same for both cases.
But stagnation pressure
at the exit of the adiabatic process
(P02 ) will be less than
isentropic pressure (P02 ' ) .
This is due to friction
and irresversibilities. But
stagnation temperature remains constant.
15. A plane travels at a speed of 2400 KM/h in an
atmosphere of 5°C, find the mach angle.
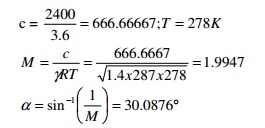
16.Define
mach angle and mach wedge.
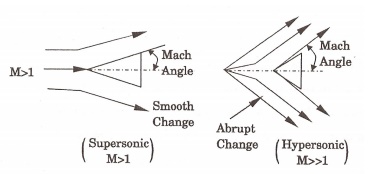
Mach
angle is formed, when an object is moving with supersonic speed. The wave
propagation and changes are smooth. When an object is moving with hypersonic
speed the changes are abrupt is shown in Fig. Hence for a supersonic flow over
two – dimensional object “mach wedge” is used instead of “mach cone”.
17. How
will you illustrate the role of mach number as a measure of compressibility?
If the
flow is assumed to be incompressible, the value of pressure co-efficient (or) compressibility
factor obtained by Bernoulli equation is unity.

By substituting different values of M, we can get
different values of compressibility factor and is given in the table.
In the above table, when M increases, the
compressibility factor also increases from the initial value 1. Thus the role
of mach number is a measure of compressibility.
18. What
is meant by isentropic flow with variable area?
A steady one dimensional isentropic flow in a
variable area passages is called “variable area flow”. The heat transfer is
negligible and there are no other irreversibilities due to fluid friction, etc.
19.
Define zone of action and zone of silence
with neat sketch.
20.Find
the sonic velocity in oxygen when it is at 110° C, γ=1.4 and molecular weight 32.
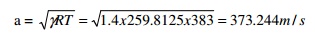
Related Topics