Basic Concepts and Isentropic Flows

Momentum Principle for a Control Volume

For a finite control volume between Sections 1 and 2 the momentum principle is,

Where F is the x-component of resultant force exerted on the fluid by the walls. Note that the momentum principle is applicable even when there are frictional dissipative processes within the control volume.

Stagnation Enthalpy

Suppose that our steady flow control volume is a set of streamlines describing the flow up to the nose of a blunt object, as in Figure

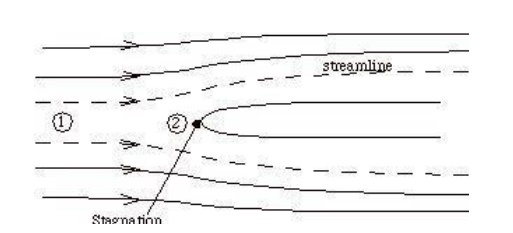
Streamlines and a stagnation region; a control volume can be drawn between the dashed streamlines and points 1 and 2. The streamlines are stationary in space, so there is no external work done on the fluid as it flows. If there is also no heat transferred to the flow (adiabatic),

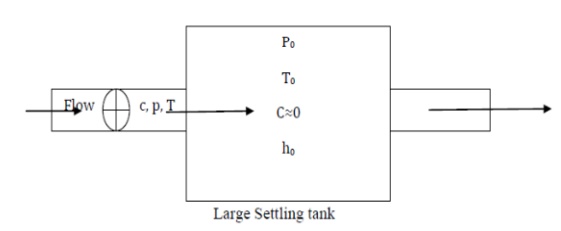
Stagnation enthalpy of a gas or vapor is its enthalpy when it is adiabatically decelerated to zero velocity at zero elevation.

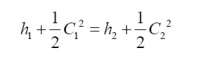
Put,

Ø h₁=h,

Ø c₁=c

Ø for the initial state h₂=h₀

Ø for the final state c₂=0

We    have   the   energy   equation   for   a   nozzle   and   diffuser   is

By substituting this in above equation,

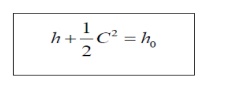
Where,

h₀ = Stagnation enthalpy h = Static enthalpy

c =  Fluid velocity m / s

In an adiabatic energy transformation process the stagnation enthalpy remain constant.

Stagnation Temperature (or) Total temperature (T₀)

Stagnation temperature of a gas when its isentropically decelerated to zero velocity at zero elevation.

We know that, Stagnation enthalpy

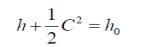
We have stagnation enthalpy and static enthalpy for a perfect gas is,

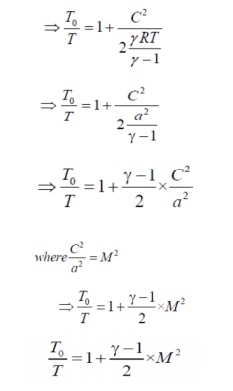
Divide by C_p through out the eqn.

Where

Ø To= stagnation temperature

Ø T = static temperature

Ø M = Mach number (C/a)

Stagnation Pressure, [Po] or total pressure

Stagnation pressure of a gas when it is isentropically decelerated to zero velocity at zero elevation. For isentropic flow.

Stagnation velocity of sound (a_o):

We know that the acoustic velocity of sound

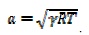
For a given value of Stagnation temperature, Stagnation velocity of sound, For stagnation condition, Put, a a_{0 ,} T T₀

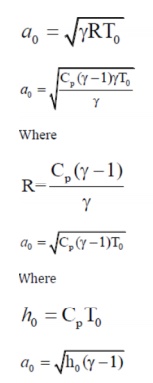
Various regions of flow

The adiabatic energy equation for a perfect gas is derived in terms of velocity of fluid(C) and Velocity of sound ao

We have stagnation enthalpy and static enthalpy for a perfect gas is h₀ c_pT₀

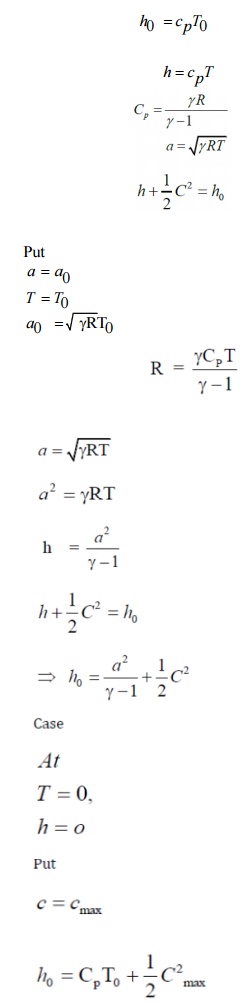
Flow Regime Classification

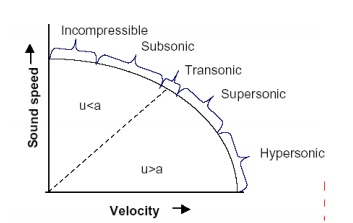
Ø Subsonic Flow (0.8 < M_o)

Ø Transonic Flow (0.8 > M0 > 1.2)

Ø Supersonic Flow (M0 > 1.2)

Ø Hypersonic Flow (M0  > 5)

Ø  Incompressible region

In incompressible flow region fluid velocity (c) is much smaller than the sound velocity (a). Therefore the Mach number (M = c/a) is very low. Eg: flow through nozzles

Ø Subsonic flow region

The subsonic flow region is on the right of the incompressible flow region. In subsonic flow, fluid velocity (c) is less than the sound velocity (a) and the Mach number in this region is always less than unity.

i.e. M = c a   1.

Eg: passenger air craft

Ø Sonic flow region

If the fluid velocity (c) is equal to the sound velocity (a), that type of flow is known as sonic flow. In sonic flow Mach number value is unity.

M = c a = 1   c  a. Eg: Nozzle throat

Ø Transonic flow region

If the fluid velocity close to the speed of sound, that type of flow is known as transonic flow .In transonic flow, Mach number value is in between 0.8 and 1.2. i.e.0.8 < M < 1.2.

Ø Supersonic flow region

The supersonic region is in the right of the transonic flow region. In supersonic flow, fluid velocity (c) is more than the sound velocity (a) and the Mach number in this region is always greater than unity.

i.e. M = c/a >1.Eg: military air crafts

Hypersonic flow region

In hypersonic flow region, fluid velocity (c) is much greater than sound velocity (a).In this flow, Mach number value is always greater than 5.

i.e. M = c/a >5. Eg: rockets

Reference Velocities

In compressible flow analysis it is often convenient to express fluid velocities is non dimensional forms.

Ø       Local velocity of sound

Ø       Stagnation velocity of sound

Ø       Maximum velocity of fluid

Ø       Critical velocity of fluid/sound. C^*=a^*

1.Maximum velocity of fluid:

From adiabatic energy equation has two components of the total energy: the enthalpy h and the kinetic energy .If kinetic energy is absent the total energy is entirely energy represented by the stagnation enthalpy h0 .the other extreme conditions which can be conceived is when the entire energy is made up of kinetic energy only=0 and C = C_max. The fluid velocity (C_max) corresponding to this condition is the maximum velocity that would be achieved by the fluid when it is accelerated to absolute zero temperature (T = 0, T = 0) in an imaginary adiabatic expansion process.

2 Critical velocity of sound

It is the velocity of flow that would exist if the flow is isentropically accelerated or decelerated to unit Mach number (critical condition).

We have

Considering the *section (where M = 1) and its stagnation section M 1

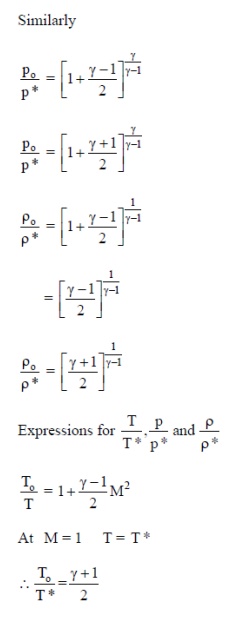
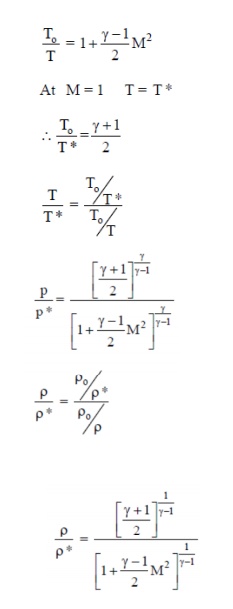
Mach number

In fluid mechanics, Mach number (M or Ma) is a dimensionless quantity representing the ratio of speed of an object moving through a fluid and the local speed of sound.

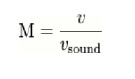
Mach Cone

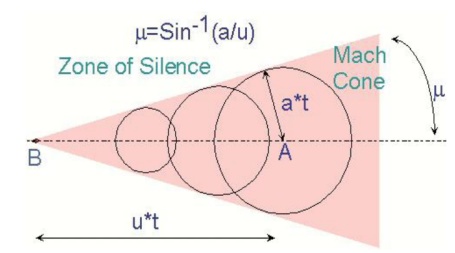
A conical surface that bounds the region in a supersonic flow of gas in which the sound waves (perturbations) emanating from a point source A of the perturbations are concentrated.

Reference Mach number M^*

In the analysis of high speed flows, another Mach number called M^*is employed. It is defined as the non dymensionlizing the fluid velocity by the critical fluid velocity or the sound velocity.

That is,

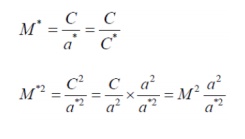
Some it is more convenient to use M^* instead of M because

(i)  at high fluid velocities M approaches infinity

(ii) M is not proportional to the velocity alone

It should be pointed out here that M^*does not mean M = 1this only other type of Mach number.

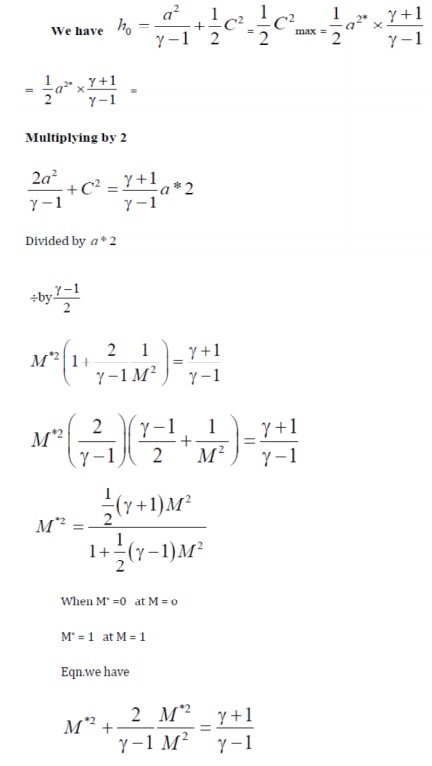
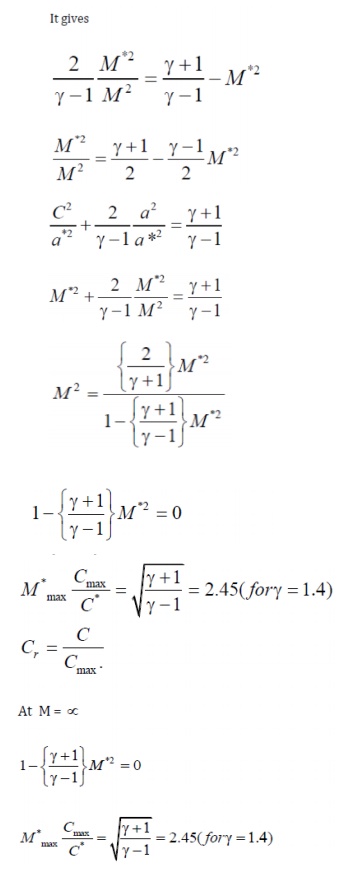
Crocco number

A non -dimensional fluid velocity can be defined by using the Maximum fluid velocity,

Isothermal Flow

Ø     Adiabatic and Reversible.

Ø     No energy added, No energy losses.

Ø     Small and gradual change in flow variables.

The earliest reference to is other mal flow was found in Shapiro’s Book. The model Suggests that the choking occurs at 1 /√kanditappearsthatShapirowasthefirstoneto realize this difference compared to the other models. In reality, the flow is choked somewhere between 1 Root of k to one for cases that are between Fanno (adiabatic) and isothermal flow. This fact was evident in industrial applications where the expectation of the choking is at Mach one, but can be explained by choking at a lower Mach number. No experimental evidence, known by the undersigned, was ever produced to verify this finding.

Law of conservation of momentum (Newton’s Second Law) Law of conservation of momentum to a system

Assumptions

Ø     1 - D flow

Ø     Steady flow

Ø     Higher order terms (Hot’s) are neglected

Ø     The fluid is invicid (M = 0)

Ø     Compressible fluid

^Fxx - This represents the summation of all forces acting on CV and includes surface and body forces. Surface forces are of normal and tangential forms. Since the fluid is invicid shear force (tangential) = 0

Figure above shows a flow through CV. All fluid properties at inlet and exit are represented. Various forces act ing are also represented in their respective direction at the appropriate locations.

Problems

1) Atm air at 1.1×10⁵ N/m² and 65^oC is accelerated isentropically to a mach number of 1.

Find final temp, pressure and flow velocity.

Ans.Assume, the given state is the stagnation state, From data book, is entropic table, K = 1.4

T = T* = 8.834 × To = 0.834 × 338

T = 281.9 K

Final temperature T* = 281.9 K

P = P* = Po × 0.528

=  1.1 × 10⁵ × 0.528

0.581 × 10⁵ N/m²

Flow through Nozzles

A nozzle is a duct that increases the velocity of the flowing fluid at the expense of pressure drop. A duct which decreases the velocity of a fluid and causes a corresponding increase in pressure is a diffuser. The same duct may be either a nozzle or a diffuser depending upon the end conditions across it. If the cross-section of a duct decreases gradually from inlet to exit, the duct is said to be convergent. Conversely if the cross section increases gradually from the inlet to exit, the duct is said to be divergent. If the cross-section initially decreases and then increases, the duct is called a convergent-divergent nozzle. The minimum cross-section of such ducts is known as throat. A fluid is said to be compressible if its density changes with the change in pressure brought about by the flow. If the density does not changes or changes very little, the fluid is said to be incompressible. Usually the gases and vapors are compressible, whereas liquids are incompressible.

Nozzle:

A nozzle is primarily used to increase the flow velocity.

The velocity is increased at the cost of drop in enthalpy. If an ideal gas is flowing through the nozzle, the exit velocity Ve can be expressed in terms of inlet and outlet pressure and temperatures by making use of the relations

Diffuser:

A diffuser can be thought of as a nozzle in which the direction of flow is reversed.

For an adiabatic diffuser, Q and Wsh are zero and the first law reduces to

The diffuser discharges fluid with higher enthalpy. The velocity of the fluid is reduced.

Ø                 Example of a reversible process:

– Slow compression of air in a balloon does work on the air inside the balloon, and takes away energy from the surroundings - When the balloon is allowed to expand, the air inside and the surrounding air are both restored to original conditions

Example of an irreversible process:

Heat flows from hot to cold, never in the opposite direction; Most conductive and viscous processes are irreversible Stagnation point is thus when fluid is brought to stagnant state (eg, reservoir)

Stagnation properties can be obtained at any point in a flow field if the fluid at that point were decelerated from local conditions to zero velocity following an isentropic (frictionless, adiabatic) process

Pressure:          p0

Temperature:    T0

Density:            ρ0

Ø     If a fluid were brought to a complete stop (C 2 = 0)

Ø     Therefore, h0 represents the enthalpy of a fluid when it is brought to rest adiabatically.

Ø     During a stagnation process, kinetic energy is converted to enthalpy.

Ø     Properties at this point are called stagnation properties (which are identified by subscript 0)

If the process is also reversible, the stagnation state is called the isentropic stagnation state.

Stagnation enthalpy is the same for isentropic and actual stagnation states

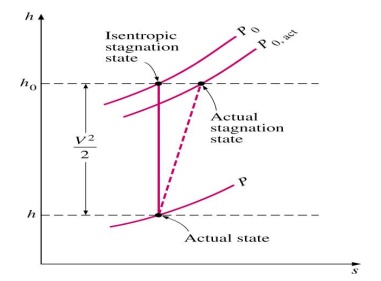
Actual stagnation pressure P0,act is lower than P0 due to increase in entropy s as a result of fluid friction. Nonetheless, stagnation processes are often approximated to be isentropic, and isentropic properties are referred to as stagnation properties

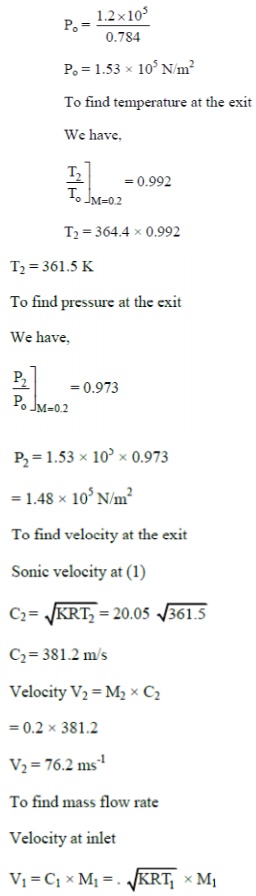
Q 9) Air is discharged from a reservoir at Po = 6.91 Kgf/cm²and to = 325^oC through a nozzle to an exit pressure of 0.98 Kgf/cm² . If the flow rate is 1 kg/s, find the throat area, pressure and velocity. Also find the exit area, exit temperature and exit velocity.

Ans

Exit Mach number M_e] = 1.93

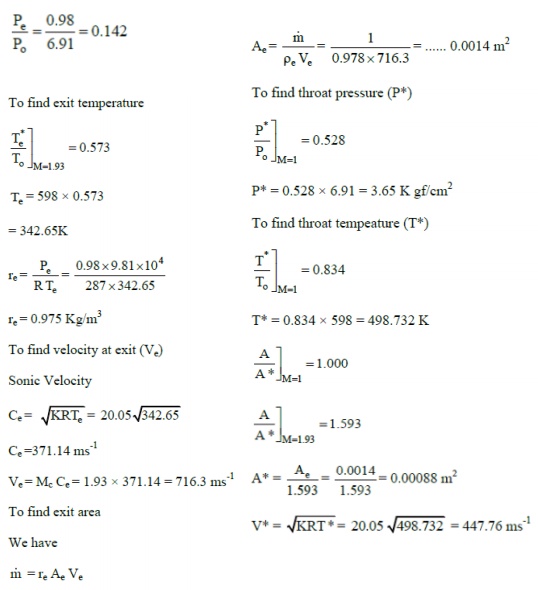
Q 10) Air flows isentropically through a C.D. The inlet conditions are pressure 700 KN/m², temperature 320^oC, velocity 50 m/s. The exit pressure is 10⁵KN/m² and the exist area is 6.25 cm². Calculate

i)                   Mach number, temperature and velocity at exit

ii)                  Pressure, temperature and velocity at throat

iii)              Mass flow rate

iv)              Throat area

Ans: To find the exit mach number (M2)

Sonic velocity at inlet

Tutorial Problems:

1.The pressure, temperature and Mach number at the entry of a flow passage are 2.45 bar, 26.5° C and 1.4 respectively. If the exit Mach number is 2.5 determine for adiabatic flow of perfect gas (γ =1.3, R=0.469 KJ/Kg K).

2. Air flowing in a duct has a velocity of 300 m/s ,pressure 1.0 bar and temperature 290 k. Taking γ=1.4 and R =287J/Kg K determine: 1) Stagnation pressure and temperature, 2) Velocity of sound in the dynamic and stagnation conditions, 3) Stagnation pressure assuming constant density.

3. A nozzle in a wind tunnel gives a test –section Mach number of 2.0 .Air enters the nozzle from a large reservoir at 0.69 bar and 310 k .The cross –sectional area of the throat is1000cm²

.Determine the following quantites for the tunnel for one dimensional isentropic flow 1) Pressures,temperature and velocities at the throat and test sections, 2) Area of cross- sectional of the test section , 3) Mass flow rate, 4) Power rate required to drive the compressor.

4.Air is discharged from a reservoir at Po =6.91bar and To =325°c through a nozzle to an exit

pressure of 0.98 bar .If the flow rate is 3600Kg/hr determine for isentropic flow: 1)Throat area, pressure,and velocity, 2)Exit area,Mach number ,and 3)Maximum velocity.

5.Air flowing in a duct has a velocity of 300 m/s ,pressure 1.0 bar and temperature 290 K. Taking γ=1.4 and R =287J/Kg K determine: 1)Stagnation pressure and temperature, 2)Velocity

of sound in the dynamic and stagnation conditions 3)Stagnation pressure assuming constant density.

6.A conical diffuser has entry and exit diameters of 15 cm and 30cm respectively. Pressure ,temperature and velocity of air at entry are 0.69bar,340 k and 180 m/s respectively . Determine 1) The exit pressure, 2) The exit velocity and 3) The force exerted on the diffuser walls.Assume isentropic flow,γ =1.4,Cp =1.00 KJ Kg-K