Chapter: Civil : Strength of Materials : Advanced Topics In Bending of Beams
Important Questions and Answers: Advanced Topics In Bending of Beams
1. What
are the assumptions made in the analysis of curved bars?
1.Plane sections remain plane during bending.
2.The material obeys Hooke's law.
3.Radial strain is negligible.
4.The fibres are
free to expand or contract without any constraining effect from the adjacent
fibres.
2.
Write the formula for stress using Winkler-Bach theory?

3. Define
unsymmetrical bending.
If the plane of
loading or that of bending, does not lie in (or parallel to) a plane that
contains the principal centroidal axisof the cross-section, the bending is
called unsymmetrical bending.
4.
What are the reasons for
unsymmetrical bending?
1.The section is
symmetrical but the load line is inclined to both the principal axes. 2.The
section itself is unsymmetrical and the load line is along the centroidal axis.
5.
How will you calculate the stress
due to unsymmetrical bending?
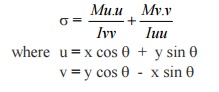
6.
How will you calculate the distance
of neutral axis from centroidal axis.

-ve sign shows that neutral axis is below the
centroidal axis.
7. How will you calculate the angle of inclination of neutral axis
with respect to principal axis?
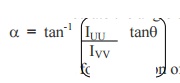
8. Write the formula for
deflection of a beam causing unsymmetrical bending.

Where K = a constant depending upon
the end conditions of the beam and the position of the load along the beam
l = length of the beam
q= angle of inclination of load W with respect to VV principal
axis
9.How will you calculate the
resultant stress in a curved bar subjected to direct stress and bending stress.
?r = ?o + ?b
where so = Direct stress = P/A sb = Bending stress
10. How eill you calculate the resultant stress
in a chain link.
?r = ?o + ?b
where ?o = Direct stress = P/2A x sin q
?b = Bending stress
11. What is shear centre or angle of twist?
The shear centre
for any transverse section of the beam is the point of intersection of the
bending axis and the plane of the transverse section.
12. Who postulated the theory of curved beam?
Winkler-Bach postulated the theory of curved
beam.
13. What is the shape of
distribution of bending stress in a curved beam? The distribution of bending
stress is hyperbolic in a curved beam.
14. Where does the neutral axis lie in a curved
beam?
The neutral axis does not coincide with the
geometric axis.
15. What is the nature of stress in
the inside section of a crane hook? Tensile stress
16. Where does the maximum stress in a ring
under tension occur?
The maximum stress in a ring under tension
occurs along the line of action of load.
17. What is the most suitable
section for a crane?
Trapezoidal section.
18. What is pure bending of a beam?
When the loads pass
through the bending axis of a beam, then there shall be pure bending of the
beam.
19.
How will you determine the product of
inertia.
The product of
inertia is determined with respect to a set of axes which are perpendicular to
each other.
The product of
inertia is obtained by multiplying each elementary area dA by its co-ordinates
x and y and integrated over the area A.
IXY = òxy dA
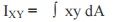
20. Define principal moment of inertia.
The perpendicular axis about which the product
of inertia is zero are called
'principal
axes' and the moments of inertia with respect to these axes are called as
principal moments of inertia.
The maximum moment of inertia is
known as Major principal moment of inertia and the minimum moment of inertia is
known as Minor principal moment of inertia.
Related Topics