Deflection Of Determinate Structures

DEFLECTION OF DETERMINATE STRUCTURES

The physical quantity work is defined as the product of force times a conjugate d isplacement, i.e., a displacement in the same d irection as the force we are considering. We are familiar with real work, i.e., the product of a r eal force and a real displacement, i.e., a force and a displacement that both actually occur. The situ ation is illustrated in Part 1 of the following figure:

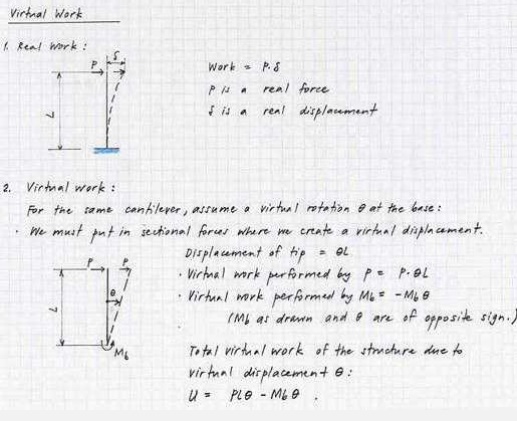
We can extend the concept of real work to a definition of virtual work, which is the product of a real force and a conjugate displacement, either real or virtual. In Part 2 of the example shown above, we assume that the cantilever column loaded with force P undergoes a virtual rotation of magnitude at its base. We compute the virtual work corresponding to this virtual displacement by summing the products of real forces times conjugate virtual displacements.

For this calculation, we must introduce unknown sectional forces at those locations where we have cut the structure to create the virtual displacement. In the example shown above, therefore, we have introduced bending moment at the base, M_b. For completeness, we would also have to

introduce a shear force V and an axial force N at the base of the column, but, as we shall see, there is no component of virtual displacement conjugate to these forces. They have therefore not been shown in the example.

We calculate the virtual displacements of the structure corresponding to all known and unknown forces. For a rotation at the base, horizontal translation of the tip of the cantilever is · L. We then multiply force times displacement and sum these products to obtain the following expression for virtual work corresponding to the assumed virtual displacement:

U = P · L ·    - M_b ·

We treat the virtual work done by force M_b as negative since the direction of M_b as drawn is opposite to the direction of the virtual rotation .

The principle of virtual work states that a system of real forces is in equilibrium if and only if the virtual work performed by these forces is zero for all virtual displacements that are compatible with geometrical boundary conditions.

For the example given in the previous subsection, this implies that the virtual work of the simple cantilever, U, must be zero for the system to be in equilibrium:

U = P · L ·    - M_b ·    = 0

Since    is nonzero, it follows that Mb = P • L, which is precisely the familiar expression for

bending moment at the base of a cantilever loaded with force P at its tip.

A more general mathematical statement of the principle of virtual work is as follows:

Let Qi be a set of real loads acting on a given structure

Let Ri be the corresponding real support reactions

Let Mi, Vi, and Ni be the sectional forces (bending moment, shear, and axial force) introduced at

the locations where the structure has been cut to allow it to undergo a virtual displacement.

Let   Qi,   Ri,   Mi,   Vi, and   Ni be virtual displacements compatible with the geometrical

boundary conditions and conjugate to the forces defined previously.

Then the structure is in equilibrium if and and only if:

(Q_i·  _Qi) +   (R_i·  _Ri) +   (M_i·  _Mi) +   (V_i·  _Vi) +   (N_i·  _Ni) = 0

Virtual Work

Virtual work is defined as the f ollowing line integral

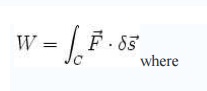
Where

C is the path or curve tra versed by the object, keeping all constraints sati sfied;

 the force vector : 

 the infinitesimal v irtual displacement vector : 

Virtual work is therefore a special case of mechanical work. For the work to be called virtual, the motion undergone by the system must be compatible with the system's const raints, hence the use of a virtual displacement.

One of the key ideas of Lagrangian mechanics is that the virtual work done by th e constraint forces should be zero. This is a reasonable assumption, for otherwise a physical system might gain or lose energy simply by being constrained (imagine a bead on a stationary hoop moving faster and faster for no apparent reason)!

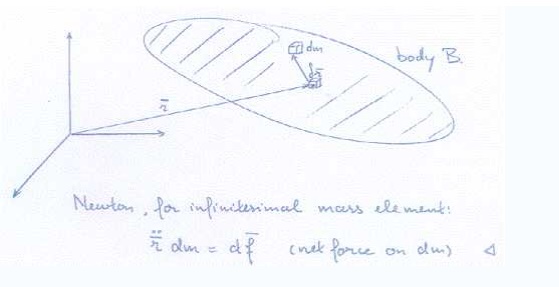
The idea of virtual work also plays a key role in interpreting D'Alembert's principle:

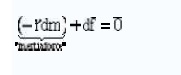
Equilibrium of forces ('staic' tre atment)

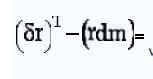 virtual wor k produced by inertia force

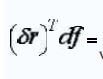  virtual work rpodu ced by net applied force.

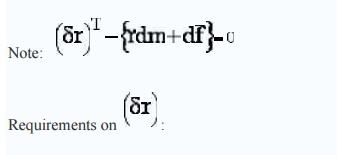
-         compatible with the kinematic constraints, but otherwise arbitrary

-         instantaneous

-         increasingly small

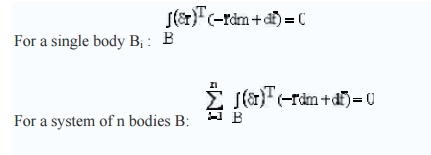
'Lagrange form of d'Alembert's Principle' 

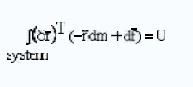
This formalism is convenient, as the constraint (non-working) loads disappear. ( forces, torques)

Where u iis the vector of independent degrees-of-freedom.

Example (i)

The motivation for introducing virtual work can be appreciated by the following simple example from statics of particles. Supposee a particle is in equilibrium under a set of force s Fx_i, Fy_i, Fz_i i =

1,2,...n:

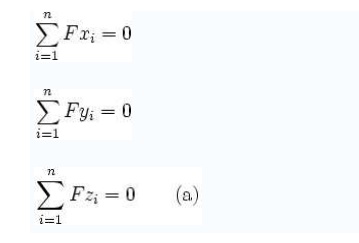
Multiplying the three equations with the respective arbitrary constants ?_x, ?_y, ?_z :

When the arbitrary constants ?_x, ?_y, ?_z are thought of as virtual displacements of the particle, then the left-hand-sides of (b) represent the virtual work. The total virtual work is:

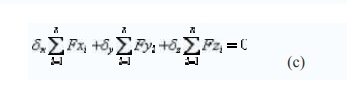
Since the preceding equality is valid for arbitrary virtual displacements, it leads back to the equilibrium equations in (a). The equation (c) is called the principle of virtual w ork for a particle. Its use is equivalent to the use of many equilibrium equations.

Applying to a deformable body in equilibrium that undergoes compatible displa cements and deformations, we can find the tottal virtual work by including both internal and external forces acting on the particles. If the mat erial particles experience compatible displacements and deformations, the work done by internal stresses cancel out, and the net virtual w ork done reduces to the work done by the applied external forces. The total virtual work i n the body may also be found by the volume integral of the product of stresses 

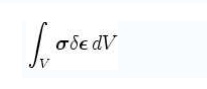
Thus, the principle of virtual wo rk for a deformable body is:

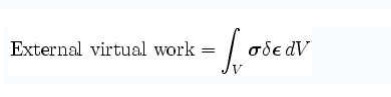
This relation is equivalent to the set of equilibrium equations written for the particles in the deformable body. It is valid irrespective of material behaviour, and hence leads to powerful applications in structural analysi s and finite element analysis.

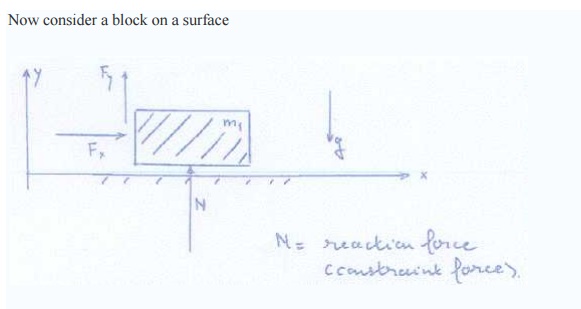
Now consider a block on a surfa       ce

Applying formula (c) gives:

Observe virtual work formalism leads directly to Newton's equation of motion i n the

kinematically allowable directio n.

Example (ii)

Two bodies connected by a rotary joint

Virtual wotk produced by these constranit loads:

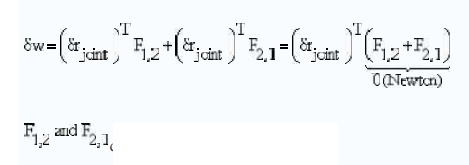
drop out of the exp ression

By assuming the contributions to virtual work produced by all forces in and an all system elements, the constraint loads dis appear.

For multi-body system, the derivation of the equatios of motion now becomes much more simple.

Degree of freedom or Kine matic Indeterminacy

Members of structure deform due to external loads. The minimum number of parameters required  to  uniquely  descr ibe the  deformed shape  of  structure  is  called  'Degree  of Freedom'. Displacements  and rotations  at  various p oints in structure are the parameters considered in describing the deformed shape of a structure. In framed structure the deformation at joints is first computed and then shape of deformed structure. Deformation at intermediate points on the structure is expressed in terms of end deformations. At supports the deformations corresponding to a reaction is zero. For example hinged support of a two dimensional system permits only rotation and translation along x and y directions are zero. Degree of freedom of a structure is expressed as a number equal to number of free displacements at all joints. For a two dimensional structure each rigid joint has three displacements as shown in

In case of three dimensional structure each rigid joint has six displacement.

•        Expression for degrees of freedom

1.       2D Frames: NDOF = 3NJ - NR        NR ?3

2.       3D Frames: NDOF = 6NJ - NR        NR ?6

3.       2D Trusses: NDOF= 2NJ - NR        NR ?3

4.       3D Trusses: NDOF = 3NJ - NR       NR ?6

Where, NDOF is the number of degrees of freedom

In 2D analysis of frames some times axial deformation is ignored. Then NAC=No. of axial condition is deducted from NDOF

Conditions of Equilibrium and Static Indeterminacy

A body is said to be under static equilibrium, when it continues to be under rest after application of loads. During motion, the equilibrium condition is called dynamic equilibrium. In two dimensional system, a body is in equilibrium when it satisfies following equation.

SFx=0 ;       SFy=0 ;       SMo=0 ---1.1

To use the equation 1.1, the force components along x and y axes are considered. In three dimensional system equilibrium equations of equilibrium are

SFx=0 ;       SFy=0 ;       SFz=0;       

SMx=0 ;     SMy=0 ;     SMz=0;       ----1.2

To use the equations of equilibrium (1.1 or 1.2), a free body diagram of the structure as a whole or of any part of the structure is drawn. Known forces and unknown reactions with assumed direction is shown on the sketch while drawing free body diagram. Unknown forces are computed using either equation 1.1 or 1.2

Before analyzing a structure, the analyst must ascertain whether the reactions can be computed using equations of equilibrium alone. If all unknown reactions can be uniquely determined from the simultaneous solution of the equations of static equilibrium, the reactions of the structure are referred to as statically determinate. If they cannot be determined using equations of equilibrium alone then such structures are called statically indeterminate structures. If the number of unknown reactions are less than the number of equations of equilibrium then the structure is statically unstable.

The degree of indeterminacy is always defined as the difference between the number of unknown forces and the number of equilibrium equations available to solve for the unknowns. These extra forces are called redundants. Indeterminacy with respect external forces and reactions are called externally indeterminate and that with respect to internal forces are called internally indeterminate.

A general procedure for determining the degree of indeterminacy of two-dimensional structures are given below:

NUK= Number of unknown forces

NEQ= Number of equations available

IND= Degree of indeterminacy

IND= NUK - NEQ

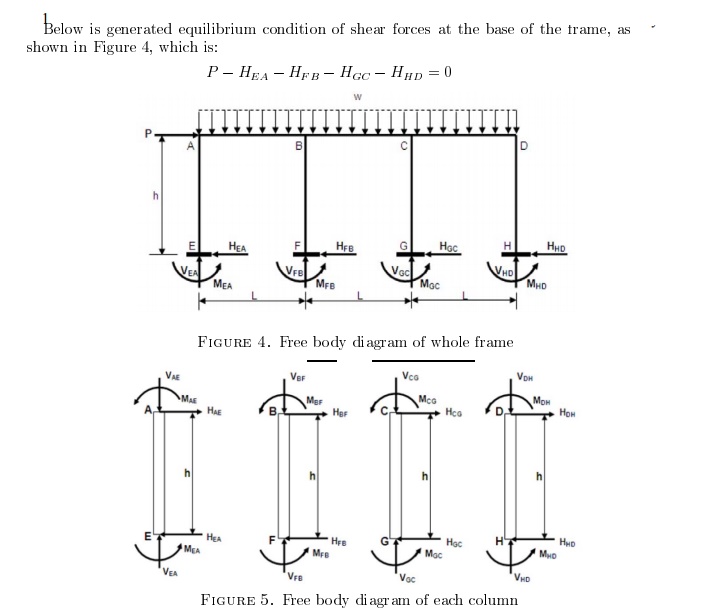
Indeterminacy of Planar Frames

For entire structure to be in equilibrium, each member and each joint must be in equilibrium (Fig. 1.9)

NEQ = 3NM+3NJ

NUK= 6NM+NR

IND= NUK - NEQ = (6NM+NR)-(3NM+3NJ)

IND= 3NM+NR-3NJ ----- 1.3