Graphical Representation of Motion along a Straight Line

Graphical Representation of Motion along a Straight Line

Plotting the distance/displacement or speed/velocity on a graph helps us visually understand certain things about time and position.

1. The distance – time graph for uniform motion

The following Table shows the distance walked by Surya at different times.

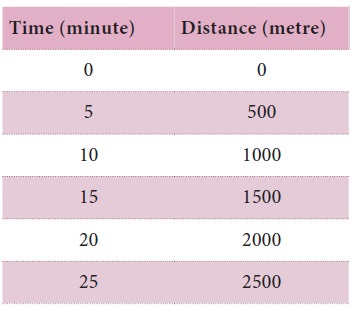
A graph is drawn by taking time along X-axis and distance along Y-axis. The graph is known as distance – time graph. When we look at the distance – time graph of Surya’s walk, we notice certain things. First, it is a straight line. We also notice that Surya covers equal distances in equal intervals of time. 

We can therefore conclude that Surya walked at a constant speed. Can you find the speed at which Surya walked, from the graph? Yes, you can. The parameter is referred to as the slope of the line.

Speed at which Surya walked = distance covered / time taken = BC/AC (From the graph)

 = slope of the straight line

 = 500 / 5 = 100 ms^-1

Steeper the slope (in other words the larger value) the greater is the speed.

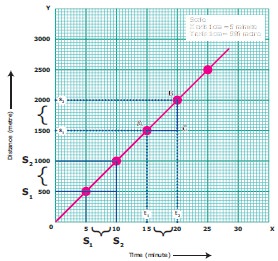
Let us take a look at the distance–time graphs of three different people – Surya walking, Monica cycling and Hari going in a car, along the same path. We know that cycling can be faster than walking and a car can go faster than a cycle. The distance – time graph of the three would be as given in the following graph. The slope of the line on the distance – time graph becomes steeper and steeper as the speed increases.

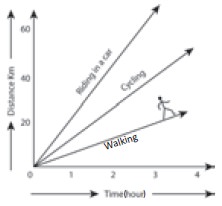
2. The distance time graph for non uniform motion

We can also plot the distance – time graph for accelerated motion (non uniform motion). Table given below shows the distance travelled by a car in a time interval of two second.

Note that the graph is not a straight line as we got in the case of uniform motion. is nature of the graph shows non – linear variation of the distance travelled by the car with time. us, the graph represents motion with non uniform speed.

3. Velocity – Time graph

The variation in velocity of an object with time can be represented by velocity – time graph. In the graph, time is represented along the X – axis and the velocity is represented along the Y – axis. If the object moves at uniform velocity, a straight line parallel to X-axis is obtained. is Graph shows the velocity – time graph for a car moving with uniform velocity of 40 km/hour.

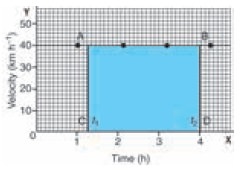
We know that the product of velocity and time gives displacement of an object moving with uniform velocity.

The area under the velocity – time graph is equal to the magnitude of the displacement.

So the distance (displacement) S covered by the car in a time interval of t can be expressed as

S = AC × CD

S = Area of the rectangle ABCD (shaded portion in the graph)

We can also study about uniformly accelerated motion by plotting its velocity – time graph. Consider a car being driven along a straight road for testing its engine. Suppose a person sitting next to the driver records its velocity for every 5 seconds from the speedometer of the car. The velocity of the car in ms-1 at different instants of time is shown in the Table below.

In this case, the velocity – time graph for the motion of the car is shown in graph (straight line). The nature of the graph shows that the velocity changes by equal amounts in equal intervals of time. Thus, for all uniformly accelerated motion, the velocity – time graph is a straight line.

One can also determine the distance moved by the car from its velocity – time graph. The area under the velocity – time graph gives the distance (magnitude of displacement) moved by the car in a given interval of time.

Since the magnitude of the velocity of the car is changing due to acceleration, the distance S travelled by the car will be given by the area ABCDE under the velocity – time graph. That is

S = area ABCDE

 = area of the rectangle ABCD + area of the triangle ADE

S = (AB × BC) + ½ (AD × DE)

The area ABCDE can also be calculated by considering the shape as trapezium. Area of the quadrangle ABCDE can also be calculated by calculating the area of trapezium ABCDE. It means

S = area of trapezium ABCDE

 = ½ × sum of length of parallel sides × distance between parallel sides

S = ½ × (AB + CE) × BC

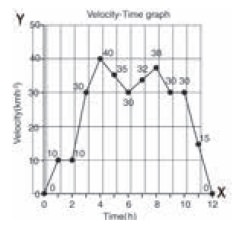
In the case of non uniformly accelerated motion, distance – time graph, velocity – time graphs can have any shape as shown in Figure below: