Equations of Motion

Equations of Motion

Newton studied the motion of an object and gave a set of three equations of motion. These equations relate the displacement, velocity, acceleration and time of an object under motion. An object is in motion with initial velocity u attains a final velocity v in time t due to acceleration a, with displacement s.

The three equations of motion can be written as,

v = u + at

s = ut + ½ a t²

 v²= u² + 2as

Let us try to derive these equations by graphical method.

Equations of motion from velocity – time graph:

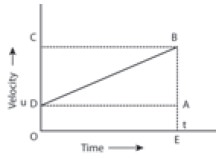
Graph shows the change in velocity with time for an uniformly accelerated object. The object starts from the point D in the graph with velocity u. Its velocity keeps increasing and after time t it reaches the point B on the graph.

The initial velocity of the object = u = OD = EA

The nal velocity of the object = v = OC = EB Time = t = OE = DA

Also from the graph we know that, AB = DC

1. First equation of motion

By definition, acceleration = change in velocity / time

= (final velocity – initial velocity)/time

= (OC – OD) / OE

= (OC – OD) / OE = DC / OE

a = DC / t

DC = AB = at

From the graph EB = EA + AB

v = u + at                 ………(1)

This is first equation of motion.

2. Second equation of motion

From the graph the distance covered by the object during time t is given by the area of quadrangle DOEB

s = area of the quadrangle DOEB

= area of the rectangle DOEA + area of the triangle DAB

= (AE × OE) + (1/2 × AB × DA)

s = ut + ½ at²       ….(2)

This is second equation of motion.

3. Third equation of motion

From the graph the distance covered by the object during time t is given by the area of the quadrangle DOEB. Here DOEB is a trapezium. Then

S = area of trapezium DOEB

= ½ × sum of length of parallel side × distance between parallel sides

= ½ × (OD + BE) × OE

S = ½ × (u + v) × t

since a = (v – u) / t or t = (v – u)/a

Therefore s = ½ × (v + u) × (v – u)/a

2as = v ² – u²

v² = u² + 2as         ……(3)

This is third equation of motion.

Motion of objects under the influence of gravitational force of the earth – Freely falling body:

Activity 7

Take a large stone and a small eraser. Stand on the top of a table and drop them simultaneously from the same height? What do you observe?

Activity 8

Take a small eraser and a sheet of paper. Stand on the top of a table and drop them simultaneously from the same height? What do you observe?

Activity 9

Take two sheets of paper having same mass. Now, crumple one of the sheets into a ball and drop the sheet and the ball from the same height. What do you observe?

In activity 7, both the stone and the eraser have reached the surface of the earth almost at the same time but in activity 8, the eraser reaches first, the sheet of paper reaches later. In activity 9, the paper crumpled into a ball reaches ground first and plain sheet of paper reaches later, although they have equal mass. Do you know the reason? When all these objects are dropped in the absence of air medium (vacuum), all would have reached the ground at the same time. In air medium, due to friction, air offers resistance to the motion of free falling objects. The resistance offered by air is negligibly small when compared to the gravitational pull acting on the stone and rubber (in activity 7). Hence, they reach the ground at the same time. But, in activity 8, the air resistance exerted on the sheet of paper is much higher than that on the eraser. Again in activity 9, the air resistance offered to the plain sheet of paper is much higher than that offered to the paper ball. This is because the magnitude of air resistance depends on the area of objects exposed to air. 

If we do experiment in a tall glass jar from which air has been sucked out, both the paper and the eraser would fall at the same rate. Galileo dropped different objects from the top of the Leaning Tower of Pisa in Italy to prove the same. We know that an object experiences acceleration during free fall. This acceleration experienced by an object is independent of mass. This means that all objects hollow or solid, big or small, should fall at the same rate.

The equation of motion for a freely falling body can be obtained by replacing ‘a’ in equations 1 to 3 with g, the acceleration due to gravity. For an object falling freely, its initial velocity u = 0. Thus we get the following equations

v = gt, s = ½ gt², v² = 2gh

when we through an object vertically upwards, it moves against the acceleration due to gravity. Hence g is taken to be –g in such cases.

Uniform circular motion

If you carefully observe, on being released the stone moves along a straight line tangential to the circular path. is is because once the stone is released, it continues to move along the direction it has been moving at that instant. is shows that the direction of motion changed at every point when the stone was moving along the circular path. When an object moves with constant speed along a circular path, the motion is called uniform circular motion. When an object is moving with a constant speed along a circular path, the velocity changes due to the change in direction. Hence it is an accelerated motion.

Examples of uniform circular motion.

1.     Revolution of earth around the sun.

2.     Revolution of moon around the earth.

3.     The tip of the second’s hand of a clock.

If an object, moving along a circular path of radius r, takes time T to come back to its starting position, the speed v is given by,

Speed = circumference/time taken

V = 2πr/T

Giant Wheel moves in a vertical circular path.