Chapter: Medical Immunology: Antigen-Antibody Reactions
General Characteristics of the Antigen-Antibody Reaction
GENERAL CHARACTERISTICS OF THE ANTIGEN-ANTIBODY REACTION
The reaction between antigens and antibodies involves complementary binding sites on the antibody and on the antigen molecules. The sites on the antigen molecule that combine with the binding site of an antibody are known as epitopes. In the same way that the binding site is determined by different segments on the variable regions of heavy and light chains that come in close proximity due to the folding of those regions, the epitopes are also formed by discontinuous segments of an antigen molecule. Crystallographic studies have defined protein epitopes as large areas, usually involving 15–22 amino acids located on several sur-face loops. Some subsets of amino acids within the epitope are likely to contribute most of the binding energy with the antibody, while the surrounding residues provide structural complementarity, which may play a stabilizing role when antigens and antibodies interact. The significance of critical amino acids in an epitope is illustrated by the fact that antibod-ies can distinguish immunoglobulin allotypes structurally determined by one or two amino acid substitutions in the constant regions of heavy or light chains .
The interaction between the antibody-binding site and the antigen epitope involves exclusively noncovalent bonds, in a manner similar to that in which proteins bind to their cellular receptors or enzymes bind to their substrates. The binding is reversible and can be prevented or dissociated by high ionic strength or extreme pH. The following intermolec-ular forces are involved in antigen-antibody binding:
Electrostatic Bonds.Electrostatic bonds result from the attraction between oppositelycharged ionic groups of two protein side chains, for example, an ionized amino group (NH4+ ) on a lysine in the antibody and an ionized carboxyl group (COO- ) on an aspartate residue in the antigen.
Hydrogen Bonding.When the antigen and antibody are in very close proximity, rel-atively weak hydrogen bonds can be formed between hydrophilic groups (e.g., OH and C==O, NH and C==O, and NH and OH groups).
Hydrophobic Interactions.Hydrophobic groups, such as the side chains of valine,leucine, and phenylalanine, tend to associate due to van der Waals bonding and coalesce in an aqueous environment, excluding water molecules from their sur-roundings. As a consequence, the distance between them decreases, enhancing the energies of attraction involved. This type of interaction is estimated to con-tribute up to 50% of the total strength of the antigen-antibody bond.
Van der Waals Bonds. These forces depend upon interactions between the “electronclouds” that surround the antigen and antibody molecules. The interaction has been compared to that which might exist between alternating dipoles in two molecules, alternating in such a way that at any given moment oppositely ori-ented dipoles will be present in closely apposed areas of the antigen and anti-body molecules.
All these types of interactions depend on the close proximity of the antigen and anti-body molecules. For that reason, the “good fit” between an antigenic determinant and an antibody combining site determines the stability of the antigen-antibody reaction.
A. Antibody Specificity
Most of the data concerning this topic was generated in studies of the immune response to closely related haptens. Using a conjugate of m-aminobenzene sulfonate (haptenic group) with an immunogenic carrier protein, it was noticed that an animal inoculated with it would produce antibody that recognized this simple chemical group. When the antibody to m-aminobenzene sulfonate was tested for its ability to bind to the ortho, meta, and para iso-mers of aminobenzene sulfonate and to related molecules in which the sulfonate group was substituted by arsonate or carboxylate, it was noted (as shown in Table 8.1) that best reac-tivity occurred with the hapten used for immunization (m-aminobenzene sulfonate). Of the related haptens, o-aminobenzene sulfonate reacted reasonably while m-aminobenzene ar-sonate and m-aminobenzene carboxylate reacted very poorly or not at all.
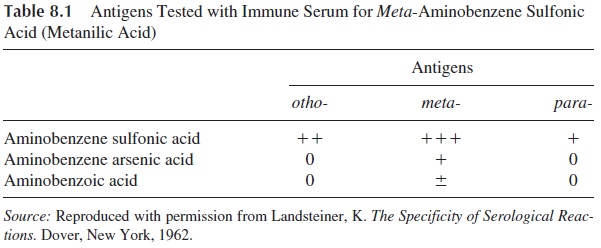
These and other experiments of the same type led to the conclusion that specificity is mainly determined by the overall degree of complementarity between antigenic determinant and antibody-binding site (Fig. 8.1); differences in the degree of complementarity de-termine the affinity of the antigen-antibody reaction.
B. Affinity
Antibody affinity can be defined as the attractive force between the complementary con-formations of the antigenic determinant and the antibody-combining site. Experimentally, the reaction is best studied with antibodies directed against monovalent haptens. The reac-tion, as we know, is reversible and can be defined by the following equation:

wherek1 is the association constant and k2 the dissociation constant.
In simple terms, Thek1/k2 ratio is the intrinsic association constant or equilibriumconstant (K). This equilibrium constant represents the intrinsic affinity of the antibody-binding sites for the hapten. High values for K will reflect a predominance of k1 over k2, or, in other words, a tendency for the antigen-antibody complex to be stable and not to disso-ciate. The equilibrium constant (K) can be defined by the equation below:
k1[Ab][Hp] = k2[AbHp]
that can be converted into:
K = k1 / k2 = [Ab.Hp] / [Ab][Hp]

where [Ab] corresponds to the concentration of free antibody-binding sites, [Hp] to the concentration of free hapten, and [Ab.Hp] to the concentration of saturated antibody-bind-ing sites.
K, also designated as affinity constant, is usually determined by equilibrium dialysisexperiments in which antibody is enclosed in a semi-permeable membrane and dialyzed against a solution containing known amounts of free hapten. Free hapten diffuses across the membrane into the dialysis bag, where it will bind to antibody. Part of the hapten inside the bag will be free, part will be bound, and the ratio of free and bound haptens depends on the antibody affinity. When equilibrium is reached, the amounts of free hapten will be identi-cal inside and outside the bag. The difference between the amount of hapten inside the bag minus the concentration of free hapten outside the bag is equal to the amount of bound hap-ten. If the molar concentration of antibody in the system is known, it becomes possible to determine the values of r (number of hapten molecules bound per antibody molecule) and c (concentration of free hapten).
Taking Eq. (3) as a starting point, if [Ab Hp] is divided by the total concentration of antibody, the quotient equals the number of hapten molecules bound per antibody molecule [r], and the quotient between the number of vacant antibody sites [Ab] divided by the total concentration of antibody equals the difference between the maximum number of antibody molecules that can be bound by antibody molecule [nor valency], and the number of hap-ten molecules bound per Ab molecule [r] at a given hapten concentration [c]. Eq. (3) can be rewritten as
K = r / [(n – r)c]

Equation (4), in turn can be rewritten as the Scatchard equation:
r / c = Kn - Kr

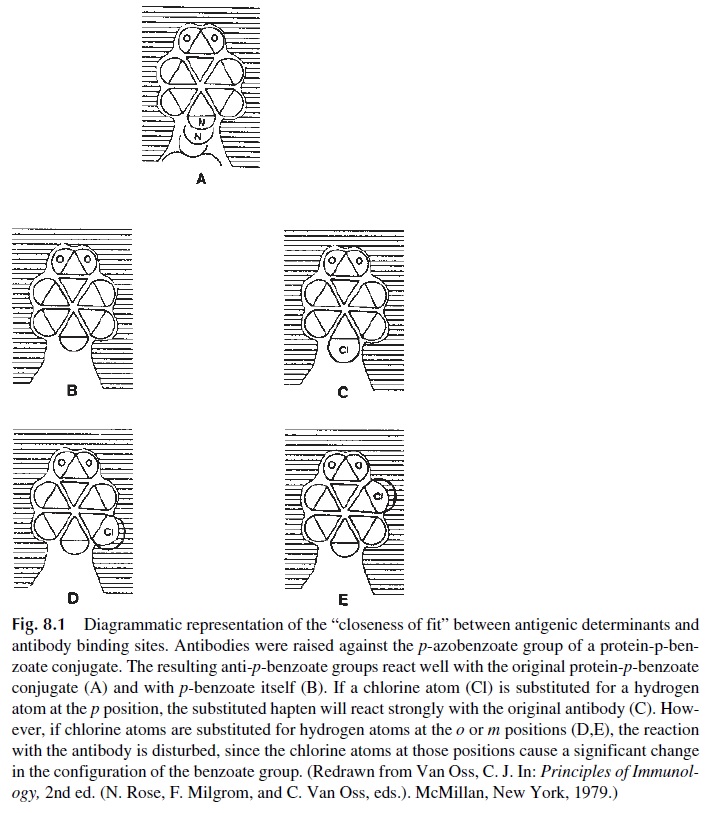
By determining r and c concentrations in a series of experiments with dialysis mem-branes carried out at different total hapten concentrations, it becomes possible, using Eq. (5), to construct what is known as a Scatchard plot, in which r/c is plotted vs. r (Fig. 8.2). It is also possible to determine the slope of the plot of r/c vs. r values that corresponds to K. The correlation between the slope and the affinity constant is also illustrated in Figure8.2. With high-affinity antibodies, r will reach saturation (r=n) at relatively low concen-trations of hapten, and the plot will have a steep slope, as shown at the left. With low-affin-ity antibodies, the stable occupancy of the antibody binding sites will require higher con-centrations of free hapten, so the r/c quotients will be considerably lower and the slope considerably less steep, as shown on the right. Since the reactants (antibodies and haptens) are expressed as moles liter -1, the affinity constant is expressed as liters mole -1 (L . mol -1).
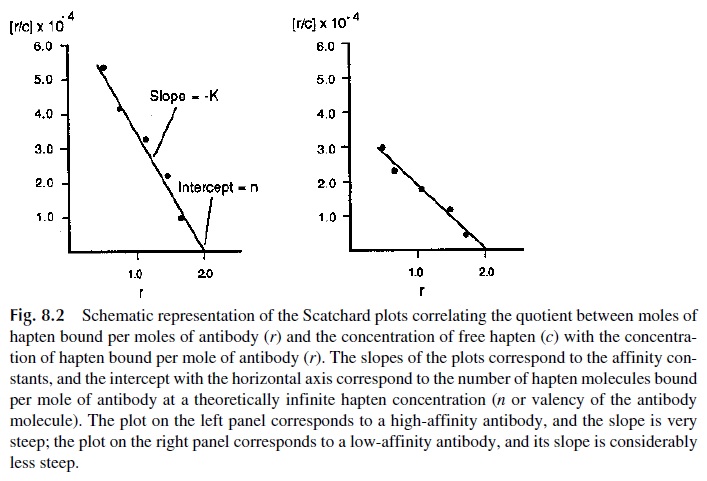
From the Scatchard plot it is obvious that at extremely high concentrations of un-bound hapten (c), r/c becomes close to 0, and the plot of r/c vs. r will intercept r on the hor-izontal axis (the interception corresponds to n, the antibody valency). For an IgG antibody and all other monomeric antibodies, the value of n is 2; for IgM antibodies, the theoretical valency is 10, but the functional valency is usually 5, suggesting that steric hindrance ef-fects prevent simultaneous occupation of the binding sites of each subunit.
In most experimental conditions, an antiserum raised against one given hapten is composed of a restricted number of antibody populations with slightly different affinity constants. Under those conditions, it may be of practical value to calculate an average in-trinsic association constant or average affinity (K0), which is defined as the free haptenconcentration required to occupy half of the available antibody-binding sites (r =n/2). Substitution of r=n/2 for r in Eq. (4) leads to the formula K0 =1/c. In other words, the average affinity constant equals the reciprocal of the free antigen concentration when anti-gens occupy half of the antibody-binding sites.
High-affinity antibodies have K0 values as high as 1010 L-mol -1. High-affinity bind-ing is believed to result from a very close fit between the antigen-binding sites and the cor-responding antigenic determinants, which favor the establishment of strong noncovalent interactions between antigen and antibody.
C. Avidity
Antibody avidity can be defined as the strength of the binding of the several different anti-bodies produced in response to an immunogen, which presents several different epitopes to the immune system.
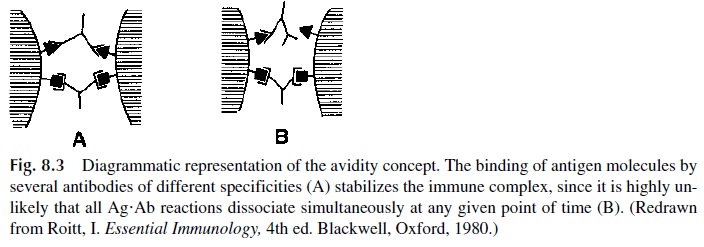
The strength of the Ag-Ab reaction is enhanced when several different antibodies bind simultaneously to different epitopes on the antigen molecule, cross-linking antigen molecules very tightly. Thus, a more stable bonding between antigen and antibody will be established due to the “bonus effect” of multiple antigen-antibody bonds (Fig. 8.3); the increased stability of the overall antigen-antibody reaction corresponds to an increased avidity.
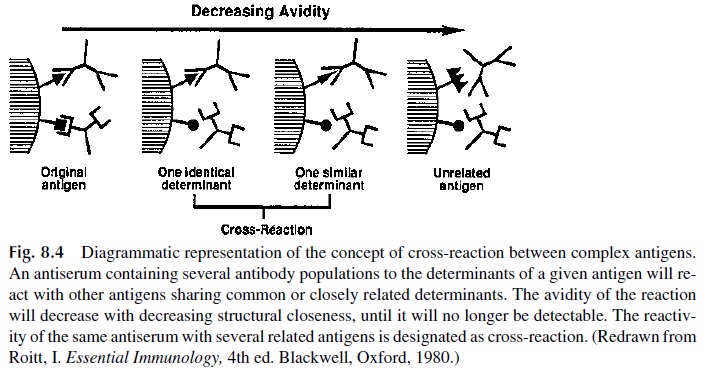
D. Cross-reactions
When an animal is immunized with an immunogen, its serum will contain several different antibodies directed to the various epitopes presented by the immunizing molecule, reflect-ing the polyclonal nature of the response. Such serum from an immune animal is known as an antiserum directed against the immunogen.
Antisera containing polyclonal antibodies can often be found to cross-react with im-munogens partially related to that used for immunization, due to the existence of common epitopes or of epitopes with similar configurations. Less frequently a cross-reaction may be totally unexpected, involving totally unrelated antigens which happen to present epitopes whose whole spatial configuration may be similar enough to allow the cross-reaction.
The avidity of a cross-reaction depends on the degree of structural similarity between the shared epitopes; when the avidity reaches a very low point, the cross-reaction will no longer be detectable (Fig. 8.4). The differential avidity of given antiserum for the original immunogen and for other immunogens sharing epitopes of similar structure is responsible for the “specificity” of the antiserum, i.e., its ability to recognize only one single immuno-gen or a few very closely related immunogens.
Related Topics