Gas Power Cycles

GAS POWER CYCLES

PREREQUISITE DISCUSSIONS

Discussion of this gas power cycles will involve the study of those heat engines in which the working fluid remains in the gaseous state throughout the cycle. We often study the ideal cycle in which internal irreversibilities and complexities (the actual intake of air and fuel, the actual combustion process, and the exhaust of products of combustion among others) are removed. We will be concerned with how the major parameters of the cycle affect the performance of heat engines. The performance is often measured in terms of the cycle efficiency.

INTRODUCTION

Ø The cycle is defined as the repeated series of operation or processes performed on a system, so that the system attains its original state.

Ø  The cycle which uses air as the working fluid is known as Gas power cycles.

Ø In the gas power cycles, air in the cylinder may be subjected to a series of operations which causes the air to attain to its original position.

Ø The source of heat supply and the sink for heat rejection are assumed to be external to the air.

Ø The cycle can be represented usually on p-V and T-S diagrams.

POWER CYCLES

Ø Ideal Cycles, Internal Combustion

Ø Otto cycle, spark ignition

Ø Diesel cycle, compression ignition

Ø Sterling & Ericsson cycles

Ø Brayton cycles

Ø Jet-propulsion cycle

Ø Ideal Cycles, External Combustion

Ø Rankine cycle

IDEAL CYCLES

Ø Idealizations & Simplifications

Ø Cycle does not involve any friction

Ø All expansion and compression processes are quasi-equilibrium processes

Ø Pipes connecting components have no heat loss

Ø Neglecting changes in kinetic and potential energy (except in nozzles & diffusers)

GAS POWER CYCLES

Ø Working fluid remains a gas for the entire cycle

Ø Examples:

Ø Spark-ignition engines

Ø Diesel engines

Ø Gas turbines

Air-Standard Assumptions

Ø Air is the working fluid, circulated in a closed loop, is an ideal gas

Ø All cycles, processes are internally reversible

Ø Combustion process replaced by heat-addition from external source

Ø Exhaust is replaced by heat rejection process which restores working fluid to initial state

ENGINE TERMS

Ø Top dead center

Ø Bottom dead center

Ø Bore

Ø Stroke

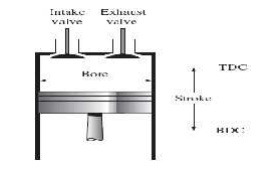
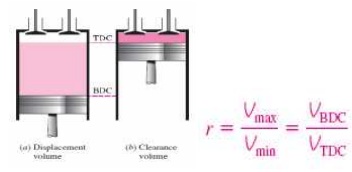
Ø Clearance volume

Ø Displacement volume

Ø Compression ratio

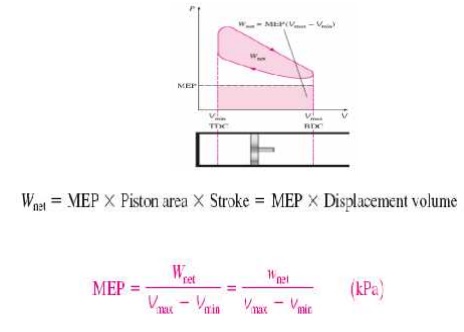
Ø Mean effective pressure (MEP)

CYCLES AND THEIR CONCEPTS

OTTO CYCLE

An Otto cycle is an idealized thermodynamic cycle that describes the functioning of a typical spark ignition piston engine. It is the thermodynamic cycle most commonly found in automobile engines. The idealized diagrams of a four-stroke Otto cycle Both diagrams

Ø Petrol and gas engines are operated on this cycle

Ø Two reversible isentropic or adiabatic processes

Ø Two  constant volume process

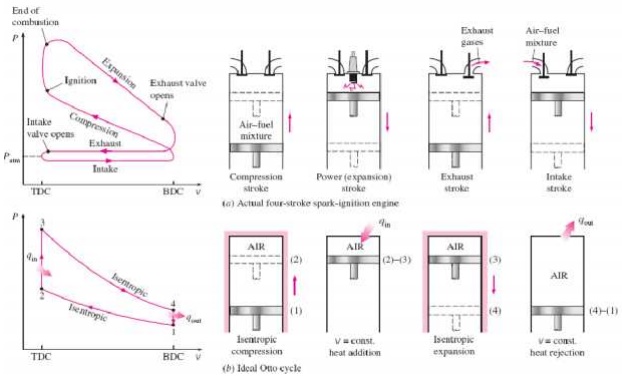
PROCESS OF OTTO CYCLE

Ø Ideal Otto Cycle

Ø Four internally reversible processes

o 1-2 Isentropic compression

o 2-3 Constant-volume heat addition

o 3-4 Isentropic expansion

o 4-1 Constant-volume heat rejection

Thermal efficiency of ideal Otto cycle:

Since V₂= V₃ and V₄ = V ₁

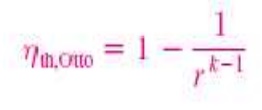
Diesel cycle

The Diesel cycle is a co mbustion process of a reciprocating internal co mbustion engine. In it, fuel is ignited by hea t generated during the compression of air in the combustion chamber, into which fuel is t hen injected.

It is assumed to have constant pressure during the initial part of the "combustion" phase The  Diesel  engine  is  a  heat  engine:  it  converts heat into work.  During  the         bottom isentropic processes (blue), energy is transferred into the system in the form of work  , W_in but by definition (isentropic) no ene rgy is transferred into or out of the system in the form of heat. During the constant pressure ( red, isobaric) process, energy enters the syste m as heat   . During the top isentropic processes (yellow), energy is transferred out of the sy stem in the form of  W_out, but by definition (isen tropic) no energy is transferred into or out of the system in the form of heat. During the constan t volume (green,isochoric) process, some of energy flows out of the system as heat through the right depressurizing process Q_out . The wor k that leaves the system is equal to the work that enters the system plus the difference between the heat added to the system and the heat that lea ves the system; in other words, net gain of wo rk is equal to the difference between the heat adde d to the system and the heat that leaves the system.

PROCESSES OF DIESEL CYCLE:

Ø 1-2 Isentropic com pression

Ø 2-3 Constant-Pres sure heat addition

Ø 3-4 Isentropic expansion

Ø 4-1 Constant-volume heat rejection

For ideal diesel cycle

Cut off ratio r_c

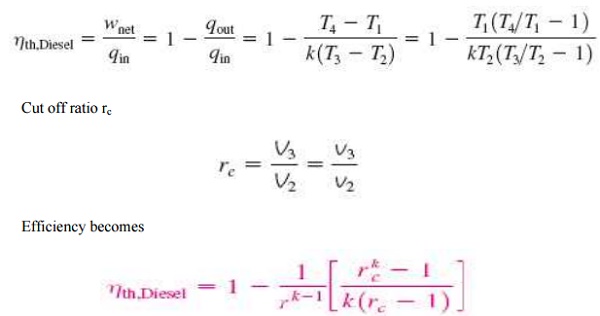
DUAL CYCLE

The dual combustion cycle (also known as the limited pressure or mixed cycle) is a thermal cycle that is a combination of the Otto cycle and the Diesel cycle. Heat is added partly at constant volume and partly at constant pressure, the advantage of which is that more time is available for the fuel to completely combust. Because of lagging characteristics of fuel this cycle is invariably used for diesel and hot spot ignition engines.

Ø Heat addition takes place at constant volume and constant pressure process .

Ø Combination of Otto and Diesel cycle.

Ø Mixed cycle or limited pressure cycle

PROCESS OF DUAL CYCLE

Ø Isentropic compression

Ø Constant-volume heat rejection

Ø Constant-pressure heat addition

Ø Isentropic expansion

Ø Constant-volume heat rejection

The cycle is the equivalent air cycle for reciprocating high speed compression ignition engines. The P-V and T-s diagrams are shown in Figs.6 and 7. In the cycle, compression and expansion processes are isentropic; heat addition is partly at constant volume and partly at constant pressure while heat rejection is at constant volume as in the case of the Otto and Diesel cycles.

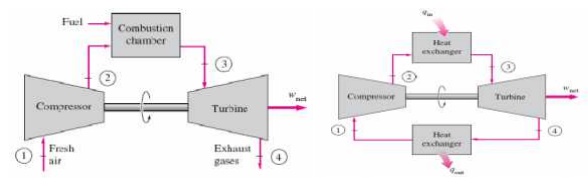
BRAYTON CYCLE

The Brayton cycle is a thermodynamic cycle that describes the workings of a constant pressure heat engine. Gas turbine engines and airbreathing jet engines use the Brayton Cycle. Although the Brayton cycle is usually run as an open system (and indeed must be run as such if internal combustion is used), it is conventionally assumed for the purposes of thermodynamic analysis that the exhaust gases are reused in the intake, enabling analysis as a closed system. The Ericsson cycle is similar to the Brayton cycle but uses external heat and incorporates the use of a regenerator.

Ø Gas turbine cycle

Ø Open vs closed system model

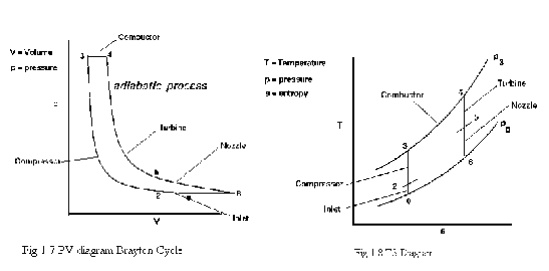
With cold-air-standard assumptions

Ø Since processes 1-2 and 3-4 are isentropic, P₂ = P₃ and P₄ = P₁

REAL TIME APPLICATIONS

PETROL ENGINES

Ø Datsun Go

Ø Hyundai Xcent

Ø Maruti Suzuki Celerio

Ø Volkswagen Vento

Ø Nissan Terrano

DIESEL ENGINES

Ø Isuzu Diesel Cars

Ø Datsun Diesel Cars

Ø Ashok Leyland Diesel Cars

GAS TURBINES

Ø Indraprastha (Delhi) CCGT Power Station India

Ø Kovilkalappal (Thirumakotai) Gas CCGT Power Station India

Ø Lanco Tanjore (Karuppur) CCGT Power Plant India

TECHNICAL TERMS

Ø TDC: Top Dead Center: Position of the piston where it forms the smallest volume

Ø BDC:  Bottom Dead Center: Position of the piston where it forms the largest volume

Ø Stroke:  Distance between TDC and BDC

Ø Bore : Diameter of the piston (internal diameter of the cylinder)

Ø Clearance volume: ratio of maximum volume to minimum volume VBDC/VTDC

Ø Engine displacement : (no of cylinders) x (stroke length) x (bore area) (usually given in cc or liters)

Ø MEP: mean effective pressure: A const. theoretical pressure that if acts on piston produces work same as that during an actual cycle

Ø Gas Power Cycles: Working fluid remains in the gaseous state through the cycle. Sometimes useful to study an idealised cycle in which internal irreversibilities and complexities are removed. Such cycles are called:Air Standard Cycles

Ø  The mean effective pressure (MEP): A fictitious pressure that, if it were applied to the piston during the power stroke, would produce the same amount of net work as that produced during the actual cycle.

Ø  Thermodynamics: Thermodynamics is the science of the relations between heat ,work and the properties of system

Ø  Boundary: System is a fixed and identifiable collection of matter enclosed by a real or imaginary surface which is impermeable to matter but which may change its shape or volume. The surface is called the boundary

Ø Surroundings: Everything outside the system which has a direct bearing on the system's behavior.

Ø Extensive Property: Extensive properties are those whose value is the sum of the values for each subdivision of the system, eg mass, volume.

Ø Intensive Property: Properties are those which have a finite value as the size of the system approaches zero, eg pressure, temperature, etc.

Ø Equilibrium: A system is in thermodynamic equilibrium if no tendency towards spontaneous change exists within the system. Energy transfers across the system disturb the equilibrium state of the system but may not shift the system significantly from its equilibrium state if carried out at low rates of change. I mentioned earlier that to define the properties of a system, they have to be uniform throughout the system.

Therefore to define the state of system, the system must be in equilibrium. Inequilibrium of course implies non-uniformity of one or more properties).

Ø Isentropic process: Isentropic process is one in which for purposes of engineering analysis and calculation, one may assume that the process takes place from initiation to completion without an increase or decrease in the entropy of the system, i.e., the entropy of the system remains constant.

Ø Isentropic flow: An isentropic flow is a flow that is both adiabatic and reversible. That is, no heat is added to the flow, and no energy transformations occur due to friction or dissipative effects. For an isentropic flow of a perfect gas, several relations can be derived to define the pressure, density and temperature along a streamline.

Ø Adiabatic heating: Adiabatic heating occurs when the pressure of a gas is increased from work done on it by its surroundings, e.g. a piston. Diesel engines rely on adiabatic heating during their compression.

Ø Adiabatic cooling: Adiabatic cooling occurs when the pressure of a substance is decreased as it does work on its surroundings. Adiabatic cooling occurs in the Earth's atmosphere with orographic lifting and lee waves, When the pressure applied on a parcel of air decreases, the air in the parcel is allowed to expand; as the volume increases, the temperature falls and internal energy decreases.

SOLVED PROBLEMS

1. In an Otto cycle air at 1bar and 290K is compressed isentropic ally until the pressure is 15bar The heat is added at constant volume until the pressure rises to 40bar. Calculate the air standard efficiency and mean effective pressure for the cycle. Take Cv=0.717 KJ/Kg K and R_univ = 8.314KJ/Kg K.

Given Data:

Pressure (P1) = 1bar = 100KN/m²

Temperature(T1) = 290K

Pressure (P2) = 15bar = 1500KN/m²

Pressure (P3) = 40bar = 4000KN/m²

Cv = 0.717 KJ/KgK

R_univ = 8.314 KJ/Kg K

To Find:

i) Air Standard Efficien cy (η_otto) ii) Mean Effective Press ure (P_m)

Solution:

Here it is g    R_univ = 8.314 KJ/Kg K

We know

2. Estimate the lose in air st andard efficiency for the diesel engine for the c ompression ratio 14 and the cutoff change s from 6% to 13% of the stroke.

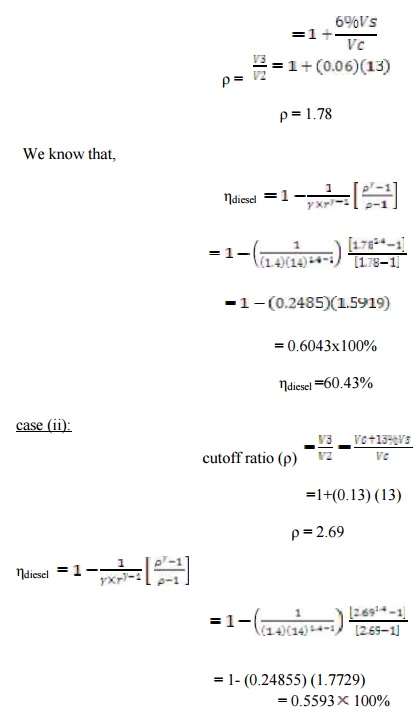
=55.93%

Lose in air standard efficiency =  (η_{diesel CASE(i)} )  -  (η_{diesel CASE(i)} )

=  0.6043-0.5593

= 0.0449

= 4.49%

3.                The compression ratio o f an air standard dual cycle is 12 and the maximum pressure on the cycle is limited to 70bar. Th e pressure and temperature of the cycle at the b eginning of compression process are 1bar a nd 300K. Calculate the thermal efficiency and M ean Effective Pressure. Assume cylinder bore = 250mm, Stroke length = 300mm, Cp=1.005K J/Kg K, Cv=0.718KJ/Kg K.

Given data:

Assume Qs₁ = Qs₂

Compression ratio (r) = 12

Maximum pressure (P₃) = (P₄) = 7000 KN/m²

Temperature (T₁) = 300 K

Diameter (d) = 0.25m

Stroke length (l) = 0.3m

To find:

Dual cycle efficiency (η_dual)

Mean Effective Pressure (P _m)

Solution:

By Process 1-2:

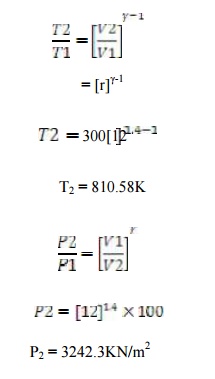
= 832.58/0.0147

P_m = 56535 KN/m²

4.A  diesel  engine  operating an  air  standard  diesel cycle  has 20cm  bore  and 30cmstroke.the clearance volu me is 420cm³.if the fuel is injected at 5% of the stroke,find the air standard efficiency.

Given Data:-

Bore diameter (d) =20cm=0.2mk

Stroke, (l) =30cm=0.3m

Clearance volume, (v₂ ) =420cm³=420/100³= m³

To Find:-

Air standard efficiency, (d_iesel) Solution:-

Compression ratio,

r = v₁/v₂

= (v_c+v_s)/v_c

We know that,

Stroke vo lume,    v_s=area*length