Chapter: Civil : Mechanics Of Fluids : Fluid Kinematics And Dynamics
Fluid Kinematics And Dynamics: Continuity Equation
Continuity
Equation
The
derivation is based on the concept of Law of conservation of mass.
Statement: The flow of fluid in a continuous flow
across a section is always a constant.
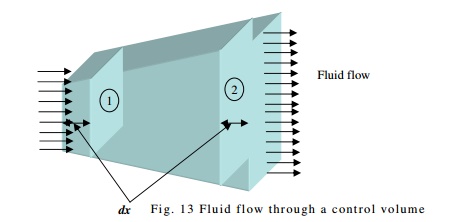
Consider an enlarging section in a fluid flow of fluid density?. Consider
two sections 1 and 2 as shown in Fig. Let the sectional properties be as under
A1and
A2 = Cross-sectional area, V1 and
V2 = Average flow velocity and ?1 and ?2 = Fluid
density at Sec 1 and 2 respectively
dt is the time taken for the fluid
to cover a distance dx The mass of fluid flowing across section
1-1 is given by
m1 = Density at section 1 x
volume of fluid that has crossed section 1
?1 x A1 x dx
Mass rate
of fluid flowing across section 1-1 is given by
m1/dt
= (Density at sec 1 x volume of fluid that has crossed sec
1)/dt
?1 x A1 x dx/dt = ?1 A1V1
…(01)
Similarly
Mass rate of fluid flowing across section 2-2 is given by
m2/dt
= ?2 x A2 x dx/dt = ?2A2
V2 …(02)
From law
of conservation of mass, mass can neither be created nor destroyed.
Hence
from Eqs. 1 and 2, we get
?1A1
V1 = ?2 A2V2
If the
density of the fluid is constant, then the equation reduces to
A1V1 = A2 V2
The above equation is discharge continuity equation in one
dimensional form for an steady, incompressible fluid flow
Continuity
Equation in three dimensional or differential forms
Consider a parallelepiped ABCDEFGH in a fluid
flow of density ? as shown
in Fig. Let the dimensions of the parallelepiped be dx, dy
and dz along x, y and z
directions respectively. Let the velocity components along x, y
and z be u, v and w respectively.
Similarly
mass rate of fluid flow leaving the section EFGH along x direction is
given by
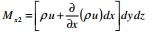
Net gain
in mass rate of the fluid along the x axis is given by the difference
between the mass rate of flow entering and leaving the control volume. i.e. Eq.
1 - Eq. 2

This expression is known as the general Equation of Continuity
in three dimensional form or differential form.
If the
fluid is incompressible then the density is constant and hence
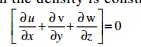
The
continuity equation in two-dimensional form for compressible and incompressible
flows are respectively as below
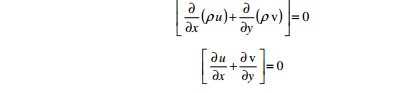
Related Topics