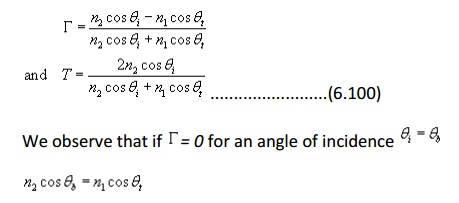Chapter: Electromagnetic Theory
Electromagnetic waves
Electromagnetic waves
In the previous chapter we introduced the equations pertaining to wave propagation and discussed how the wave equations are modified for time harmonic case. In this chapter we discuss in detail a particular form of electromagnetic wave propagation called 'plane waves'.
The Helmhotz Equation:
In source free linear isotropic medium, Maxwell equations in phasor form are,


is called the wave number or propagation constant of the medium.
Plane waves in Lossless medium:
In Cartesian coordinates each of the equations 6.1(a) and 6.1(b) are equivalent to three scalar Helmholtz's equations, one each in the components Ex, Ey and Ez or Hx , Hy, Hz.
For example if we consider Ex component we can write

A uniform plane wave is a particular solution of Maxwell's equation assuming electric field (and magnetic field) has same magnitude and phase in infinite planes perpendicular to the direction of propagation. It may be noted that in the strict sense a uniform plane wave doesn't exist in practice as creation of such waves are possible with sources of infinite extent. However, at large distances from the source, the wavefront or the surface of the constant phase becomes almost spherical and a small portion of this large sphere can be considered to plane. The characteristics of plane waves are simple and useful for studying many practical scenarios.
Let us consider a plane wave which has only Ex component and propagating along z . Since the plane wave will have no variation along the plane

are the amplitude constants (can be determined from boundary conditions).
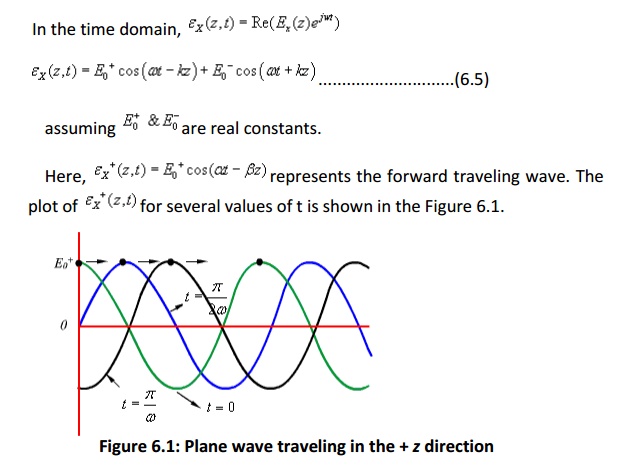
As can be seen from the figure, at successive times, the wave travels in the +z direction.


Where 'C' is the speed of light. That is plane EM wave travels in free space with the speed of light.
The wavelength l is defined as the distance between two successive maxima (or minima or any other reference points).



Which represents the magnetic field of the wave traveling in the +z direction.
For the negative traveling wave,
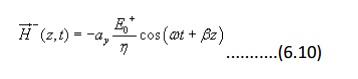
For the plane waves described, both the E & H fields are perpendicular to the direction of propagation, and these waves are called TEM (transverse electromagnetic) waves.
The E & H field components of a TEM wave is shown in Fig 6.2.
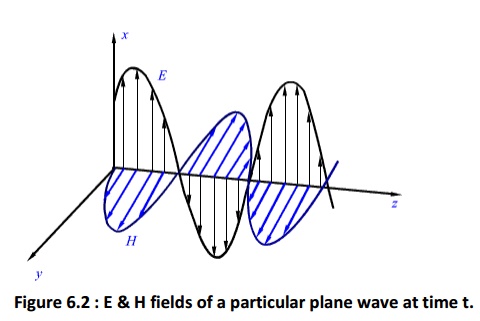
TEM Waves:
So far we have considered a plane electromagnetic wave propagating in the z-direction. Let us now consider the propagation of a uniform plane wave in any arbitrary direction that doesn't necessarily coincides with an axis.
For a uniform plane wave propagating in z-direction


z =constant denotes a plane of constant phase and uniform amplitude.
If the region under consideration is charge free,



Plane waves in a lossy medium :
In a lossy medium, the EM wave looses power as it propagates. Such a medium is conducting with conductivity σ and we can write:

We have already discussed how an external electric field can polarize a dielectric and give rise to bound charges. When the external electric field is time varying, the polarization vector will vary with the same frequency as that of the applied field. As the frequency of the applied filed increases, the inertia of the charge particles tend to prevent the particle displacement keeping pace with the applied field changes. This results in frictional damping mechanism causing power loss.
In addition, if the material has an appreciable amount of free charges, there will be ohmic losses. It is customary to include the effect of damping and





Let us now consider a plane wave that has only x -component of electric field and propagate along z .


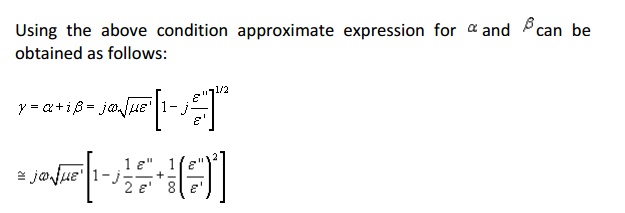
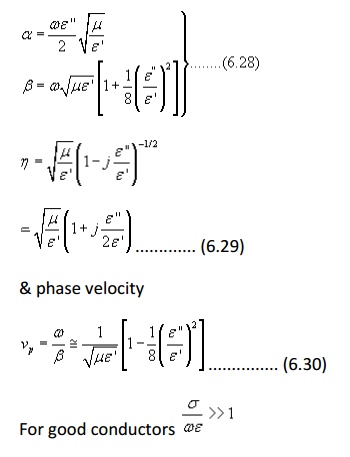


Poynting Vector and Power Flow in Electromagnetic Fields:
Electromagnetic waves can transport energy from one point to another point. The electric and magnetic field intensities asscociated with a travelling electromagnetic wave can be related to the rate of such energy transfer.
Let us consider Maxwell's Curl Equations:

the above curl equations we can write
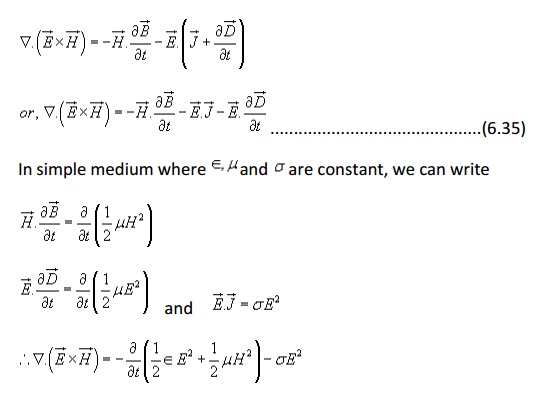
Applying Divergence theorem we can write,
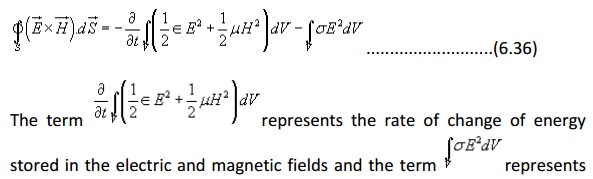
the power dissipation within the volume. Hence right hand side of the equation (6.36) represents the total decrease in power within the volume under consideration.
The left hand side of equation (6.36) can be written as
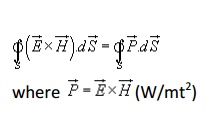
is called the Poynting vector and it represents the power density vector associated with the electromagnetic field. The integration of the Poynting vector over any closed surface gives the net power flowing out of the surface. Equation (6.36) is referred to as Poynting theorem and it states that the net power flowing out of a given volume is equal to the time rate of decrease in the energy stored within the volume minus the conduction losses.
Poynting vector for the time harmonic case:






Polarisation of plane wave:
The polarisation of a plane wave can be defined as the orientation of the electric field vector as a function of time at a fixed point in space. For an electromagnetic wave, the specification of the orientation of the electric field is sufficent as the magnetic field components are related to electric field vector by the Maxwell's equations.
Let us consider a plane wave travelling in the +z direction. The wave has both Ex and Ey components.
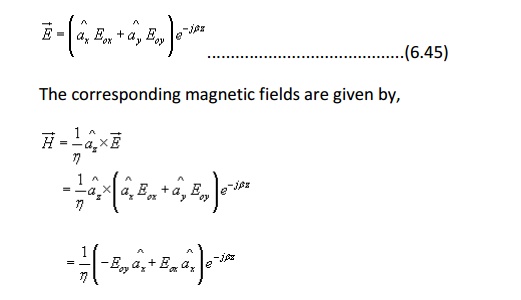
Depending upon the values of Eox and Eoy we can have several possibilities:
1. If Eoy = 0, then the wave is linearly polarised in the x-direction.
2. If Eoy = 0, then the wave is linearly polarised in the y-direction.
3.If Eox and Eoy are both real (or complex with equal phase), once again we get a linearly polarised wave with the axis of polarisation inclined at an
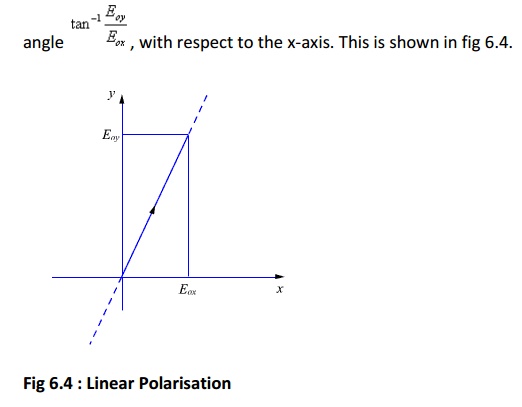



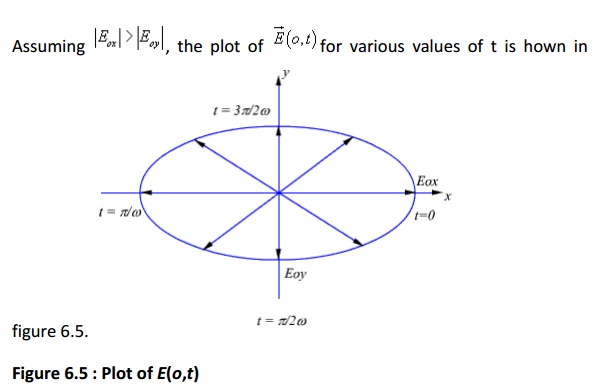
Figure 6.5 : Plot of E(o,t)
From equation (6.47) and figure (6.5) we observe that the tip of the arrow representing electric field vector traces qn ellipse and the field is said to be elliptically polarised.
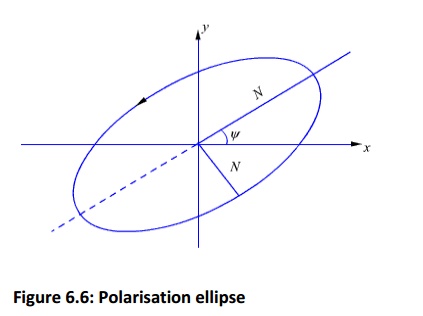
The polarisation ellipse shown in figure 6.6 is defined by its axial ratio(M/N, the ratio of semimajor to semiminor axis), tilt angle ψ (orientation with respect to xaxis) and sense of rotation(i.e., CW or CCW).
Linear polarisation can be treated as a special case of elliptical polarisation, for which the axial ratio is infinite.
In our example, if |Eox| = |Eoy|, from equation (6.47), the tip of the arrow representing electric field vector traces out a circle. Such a case is referred to as Circular Polarisation. For circular polarisation the axial ratio is unity.
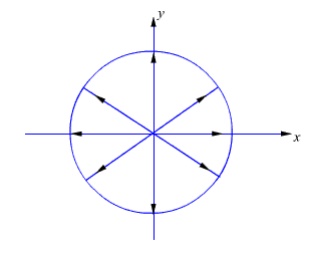
Figure 6.7: Circular Polarisation (RHCP)
Further, the circular polarisation is aside to be right handed circular polarisation (RHCP) if the electric field vector rotates in the direction of the fingers of the right hand when the thumb points in the direction of propagation-(same and CCW). If the electric field vector rotates in the opposite direction, the polarisation is asid to be left hand circular polarisation (LHCP) (same as CW).

In radio communication, different information signals can be transmitted at the same frequency at orthogonal polarisation ( one signal as vertically polarised other horizontally polarised or one as RHCP while the other as LHCP) to increase capacity. Otherwise, same signal can be transmitted at orthogonal polarisation to obtain diversity gain to improve reliability of transmission.
Behaviour of Plane waves at the inteface of two media:
We have considered the propagation of uniform plane waves in an unbounded homogeneous medium. In practice, the wave will propagate in bounded regions where several values of e,μ,σ will be present. When plane wave travelling in one medium meets a different medium, it is partly reflected and partly transmitted. In this section, we consider wave reflection and transmission at planar boundary between two media.
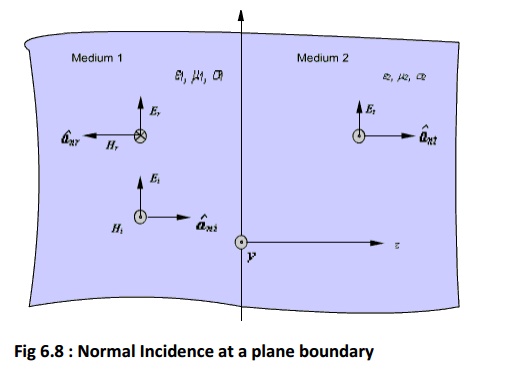


Because of the presence of the second medium at z =0, the incident wave will undergo partial reflection and partial transmission.


Applying boundary conditions at the interface z = 0, i.e., continuity of tangential field components and noting that incident, reflected and transmitted field components are tangential at the boundary, we can write

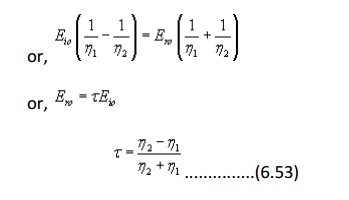
is called the reflection coefficient.
From equation (6.52), we can write

Let us now consider specific cases:
Case I: Normal incidence on a plane conducting boundary

From (6.53) and (6.54)
t = -1
and T =0
Hence the wave is not transmitted to medium 2, it gets reflected entirely from the interface to the medium 1.
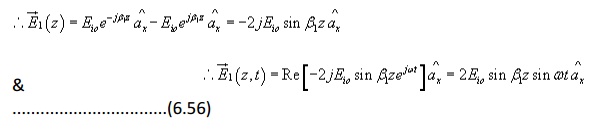
Proceeding in the same manner for the magnetic field in region 1, we can show that,

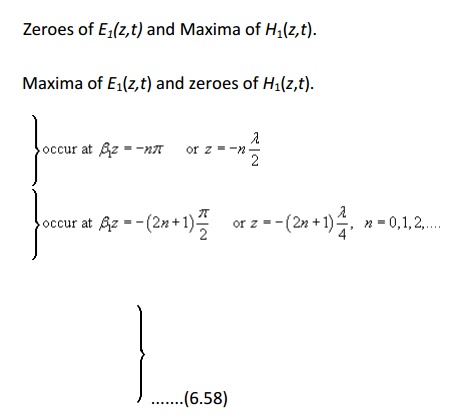
Case2: Normal incidence on a plane dielectric boundary
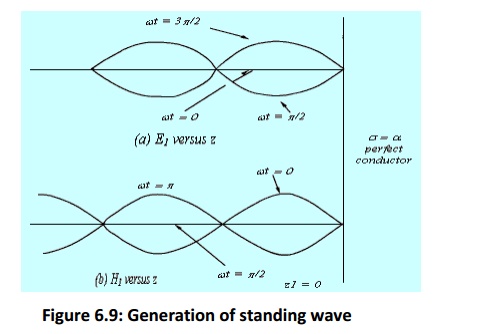
If the medium 2 is not a perfect conductor (i.e. ![]() ) partial reflection will result. There will be a reflected wave in the medium 1 and a transmitted wave in the medium 2.Because of the reflected wave, standing wave is formed in medium 1.
) partial reflection will result. There will be a reflected wave in the medium 1 and a transmitted wave in the medium 2.Because of the reflected wave, standing wave is formed in medium 1.
From equation (6.49(a)) and equation (6.53) we can writ


From (6.61), we can see that, in medium 1 we have a traveling wave component with amplitude TEio and a standing wave component with amplitude 2JEio.
The location of the maximum and the minimum of the electric and magnetic field components in the medium 1from the interface can be found as follows.
The electric field in medium 1 can be written as




Oblique Incidence of EM wave at an interface
So far we have discuss the case of normal incidence where electromagnetic wave traveling in a lossless medium impinges normally at the interface of a second medium. In this section we shall consider the case of oblique incidence. As before, we consider two cases
i. When the second medium is a perfect conductor.
ii. When the second medium is a perfect dielectric.
A plane incidence is defined as the plane containing the vector indicating the direction of propagation of the incident wave and normal to the interface. We study two specific cases when the incident electric field

is parallel to the plane of incidence (parallel polarization). For a general case, the incident wave may have arbitrary polarization but the same can be expressed as a linear combination of these two individual cases.
Oblique Incidence at a plane conducting boundary
i. Perpendicular Polarization
The situation is depicted in figure 6.10.

Since the incident wave is considered to be perpendicular to the plane of incidence, which for the present case happens to be xz plane, the electric field has only y-component.
Therefore,
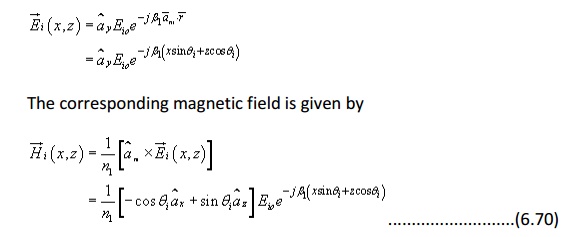
Similarly, we can write the reflected waves as


From eqns (6.76) and (6.77) we observe that

The wave propagating along the x direction has its amplitude varying with z and hence constitutes a non uniform plane wave. Further, only electric field (Bar E1) is perpendicular to the direction of propagation (i.e. x), the magnetic field has component along the direction of propagation. Such waves are called transverse electric or TE waves.
ii. Parallel Polarization:
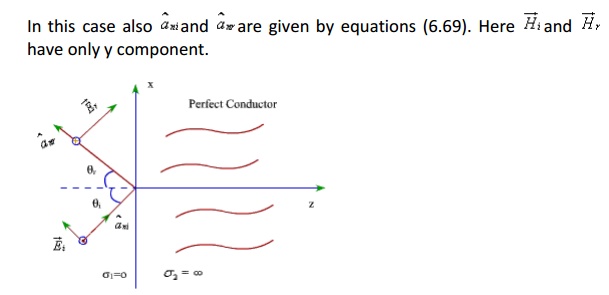
Figure 6.11: Parallel Polarization
With reference to fig (6.11), the field components can be written as:
Incident field components:

Since the total tangential electric field component at the interface is zero.
E1 (x,0) + E((x,0) =
0
Substituting these quantities in (6.79) and adding the incident and reflected electric and magnetic field components the total electric and magnetic fields can be written as

propagating wave, magnetic field is in transverse direction, such waves are called transverse magnetic or TM waves.
Oblique incidence at a plane dielectric interface
We continue our discussion on the behavior of plane waves at an interface; this time we consider a plane dielectric interface. As earlier, we consider the two specific cases, namely parallel and perpendicular polarization.
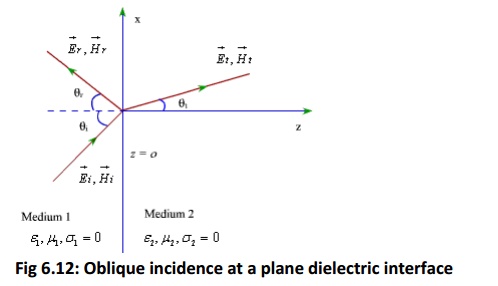
Fig 6.12: Oblique incidence at a plane dielectric interface
For the case of a plane dielectric interface, an incident wave will be reflected partially and transmitted partially.
In Fig(6.12), qi, q0, and qt corresponds respectively to the angle of incidence, reflection and transmission.
1. Parallel Polarization
As discussed previously, the incident and reflected field components can be written as


The transmitted filed can be written in terms of the transmission coefficient T
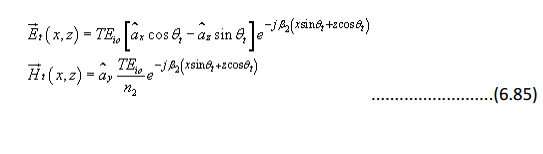
We can now enforce the continuity of tangential field components at the boundary i.e. z=0




2. Perpendicular Polarization
For this case
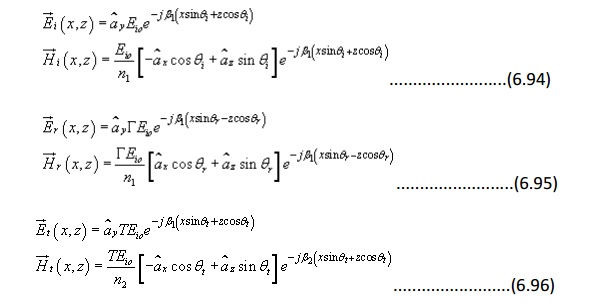
Using continuity of field components at z=0

From equation (6.99) the reflection and transmission coefficients for the perpendicular polarization can be computed as