Discrete Mathematics - Graphs

DISCRETE MATHEMATICS - GRAPHS

DISCRETE MATHEMATICS - GRAPHS

1 GRAPH & GRAPH MODELS

2 GRAPH TERMINOLOGY

3 SPECIAL TYPES OF GRAPHS

4 EULER &HAMILTONIAN GRAPH

1GRAPHS & GRAPH MODELS

DEFINITION: Graph:

A Graph G=(V,E,ɸ) consists of a non empty set v={v1,v2,…..} called the set of nodes (Points, Vertices) of the graph, E={e1,e2,…} is said to be the set of edges of the graph, and – is a mapping from the set of edges E to set off ordered or unordered pairs of elements of V.

The vertices are represented by points and each edge is represented by a line diagrammatically.

DEFINITIONS:

From the figure we have the following definitions V1,v2,v3,v4,v5 are called vertices. 

e1,e2,e3,e4,e5,e6,e7,e8 are called edges.

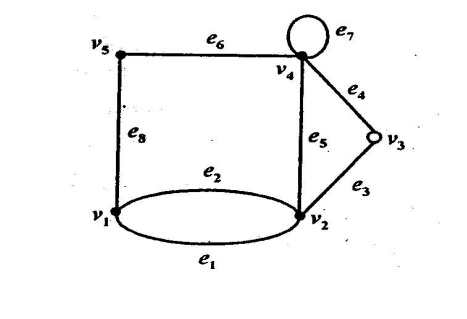
DEFINITION: Self Loop:

If there is an edge from vi to vi then that edge is called self loop or simply loop.

For example, the edge e7 is called a self loop. Since the edge e7 has the same vertex (v4) as both its terminal vertices.

DEFINITION: Parallel Edges:

If two edges have same end points then the edges are called parallel edges.

For example, the edge e1 and e2 are called parallel edges since e1 and e2 have the same pair of vertices (v1,v2) as their terminal vertices.

DEFINITION: Incident:

If the vertex vi is an end vertex of some edge ek and ek is said to be incident with vi.

DEFINITION: Adjacent edges and vertices:

Two edges are said to be adjacent if they are incident on a common vertex. In fig (i) the edges e6 and e8 are adjacent.

Two vertices vi and vj are said to adjacent if vi vj is an edge of the graph. (or equivalently (vi,vj) is an end vertices of the edge ek)

For example, in fig., v1 and v5 are adjacent vertices.

DEFINITION: Simple Graph:

A graph which has neither self loops nor parallel edges is called a simple graph.

NOTE: In this chapter, unless and otherwise stated we consider only simple undirected graphs.

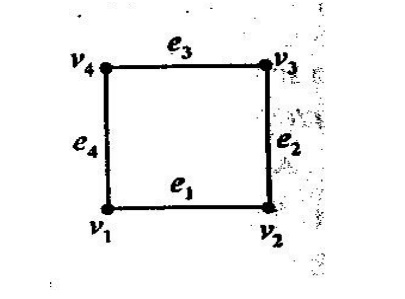
DEFINITION: Isolated Vertex:

A vertex having no edge incident on it is called an Isolated vertex. It is obvious that for an isolated vertex degree is zero.

One can easily note that Isolated vertex is not adjacent to any vertex.

If fig (ii), v5 is isolated Vertex.

DEFINITION: Pendentant Vertex:

If the degree of any vertex is one, then that vertex is called pendent vertex.

EXAMPLE:

Consider the graph

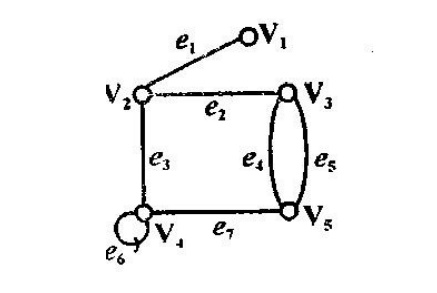
In the above undirected graph Vertices V={V1, V2, V3, V4, V5} 

Edges E={ e1,e2,….} 

And e1= < V1, V2> or < V2,V1>

e2= < V2,V3> or < V3,V2> 

e4= < V4,V2> or < V4,V2> 

e5= < V4,V4>

In the above graph vertices V1 and V2, V2 and V3, V3 and V4, V3 and V5 are adjacent. Whereas V1 and V3, V3 and V4 are not adjacent.

The edge e6 is called loop. The edges e4 and e5 are parallel edges.

Directed Edges:

In a graph G=(V,E), on edge which is associated with an ordered pair of V * V is called a directed edge of G.

If an edge which is associated with an unordered pair of nodes is called an undirected edge.

Digraph:

A graph in which every edge is directed edge is called a digraph or directed graph.

Undirected Graph:

A graph in which every edge is undirected edge is called an undirected graph.

Mixed Graph:

If some edges are directed and some are undirected in a graph, the graph is called an mixedgraph.

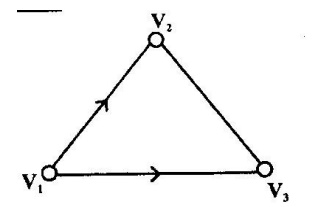
Multi Graph:

A graph which contains some parallel edges is called a multigraph.

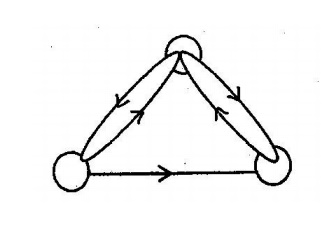
Pseudograph:

A graph in which loops and parallel edges are allowed is called a Pseudograph.

2 GRAPH TERMINOLOGY

DEFINITION: Degree of a Vertex:

The number of edges incident at the vertex vi is called the degree of the vertex with self loops counted twice and it is denoted by d (vi).

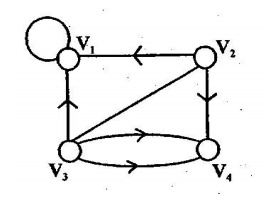
Example 1:

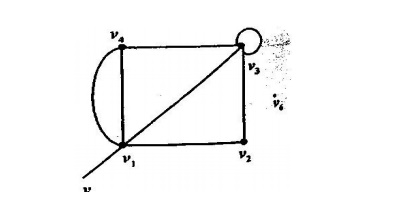
d   (v1) = 5 d (v4) = 3 

d   (v2) = 2 d (v5) = 1 

d   (v3) = 5 d (v6) = 0 

In-degree and out-degree of a directed graph:

In a directed graph, the in-degree of a vertex V, denoted by deg- (V) and defined by the number of edges with V as their terminal vertex.

The out- degree of V, denoted by deg+ (V), is the number of edges with V as their initial vertex.

NOTE: A loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.

Theorem 1: (The Handshaking Theorem)

Then

Let G= (V, E) be an undirected graph with ‘e’ edges. deg(v) = 2e

The sum of degrees of all vertices of an undirected graph is twice the number of edges of the graph and hence even.

Proof:

Since every degree is incident with exactly two vertices, every edge contributes 2 to the sum of the degree of the vertices.

Therefore, All the ‘e’ edges contribute (2e) to the sum of the degrees of vertices.

Therefore,                deg(v)= 2e

Theorem 2:

In an undirected graph, the numbers of odd degree vertices are even.

Proof:

Let V1 and V2 be the set of all vertices of even degree and set of all vertices of odd degree, respectively, in a graph G= (V, E).

Therefore,

d(v)=  d(vi)+ d(vj)

By handshaking theorem, we have Since each deg (vi) is even, is even.

As left hand side of equation (1) is even and the first expression on the RHS of (1) is even, we have the 2nd expression on the RHS must be even.

Since each deg (vj) is odd, the number of terms contained in i.e., The number of vertices of odd degree is even.

Theorem 3:

The maximum number of edges in a simple graph with ‘n’ vertices is n(n-1))/2.

Proof:

We prove this theorem by the principle of Mathematical Induction.

For n=1, a graph with one vertex has no edges. Therefore, the result is true for n=1.

edge.For n=2, a graph with 2 vertices may have at most one Therefore, 22-12=1

The result is true for n=2.

Assume that the result is true for n=k. i.e., a graph with k vertices has at most kk-12 edges.

When n=k+1. Let G be a graph having ‘n’ vertices and G’ be the graph obtained from G by deleting one vertex say v ϵ V (G).

Since G’ has k vertices, then by the hypothesis G’ has at most kk- 12 edges. Now add the vertex ‘v’ to G’. such that ‘v’ may be adjacent to all k vertices of G’.

Therefore, the total number of edges in G is, Therefore, the result is true for n=k+1.

Hence the maximum number of edges in a simple graph with ‘n’ vertices is nn-12.

Theorem 4:

If all the vertices of an undirected graph are each of degree k, show that the number of edges of the graph is a multiple of k.

Proof:

Let 2n be the number of vertices of the given graph.

Let ne be the number of edges of the given graph. By Handshaking theorem, we have

Therefore, the number of edges of the given graph is amultiple of k.

3 SPECIAL TYPES OF GRAPHS

Regular graph:

Definition: Regular graph:

If every vertex of a simple graph has the same degree, then the graph is called a regular graph.

If every vertex in a regular graph has degree k,then the graph is called k-regular.

DEFINITION : Complete graph:

In a graph, if there exist an edge between every pair of vertices,then such a graph is called complete graph.

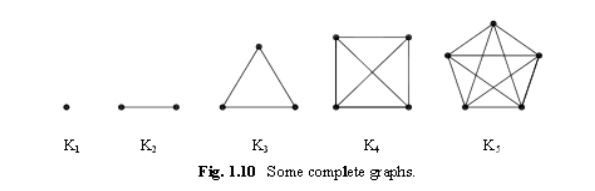
i.e., In a graph if every pair of vertices are adjacent,then such a graph is called complete graph.

If is noted that, every complete graphis a regular graph.In fact every complete graph with graph with n vertices is a (n-1)regular graph.

SUBGRAPH

A graph H =(V’, E’) is called a subgraph of G = (V, E), if V’ С V and E’ C E

In other words, a graph H is said to be a subgraph of G if all the vertices and all edges of H are in G and if the adjacency is preserve in H exactly as in G.

Hence, we have the following:

(i)    Each graph has its own subgraph.

(ii)  A single vertex in agraph G is a subgraph of G.

(iii)A single edge in G, together with its end vertices is also a subgraph of G.

(iv)                        A subgraph of a subgraph of G is also a subgraph of G.

Note: Any sub graph of a graph G can be obtained by removing certain vertices and edges from G. It is to be noted that the removal of an edges does not go with the removal of its adjacent vertices, where as the removal of any edge incident on it.

Bipartite graph:

A graph G is said to be bipartite if its vertex set V (G) can be partitioned into two disjoint non empty sets V1 and V2, V1 U V2=V(G), such that every edge in E(G) has one end vertex in V1 and another end vertex in V2. (So that no edges in G, connects either two vertices in V1 or two vertices in V2.)

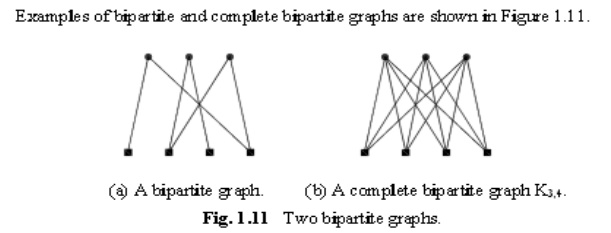
Complete Bipartite Graph:

A bipartite graph G, with the bipartition V1 and V2, is called complete bipartite graph, if every vertex in V1 is adjacent to every vertex in V2.Clearly, every vertex in V2 is adjacent to every vertex in V1.

A complete bipartite graph with bipartition is denoted by km,n.

GRAPH ISOMORPHISM

DEFINITION:

Two graphs G1 and G2 are said to be isomorphic to each other, if there exists a one-to-one correspondence between the vertex sets which preserves adjacency of the vertices.

Note: If G1 and G2 are isomorphic then G1 and G2 have,

(i)                         The same number of vertices. 

(ii)                      The same number of edges 

(iii)                   An equal number of vertices with a given degree. 

Note: However, these conditions are not sufficient for graph isomorphism.

ISOMORPHISM AND ADJACENCY:

RESULT 1:

Two graphs are isomorphic if and only if their vertices can be labeled in such a way that the corresponding adjacency matrices are equal.

RESULT 2:

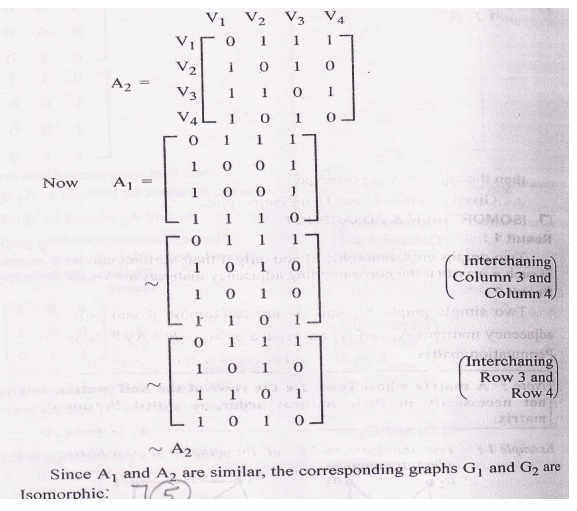
Two simple graphs G1 and G2 are isomorphic if and only if their adjacency matrices A1 and A2 are related A1=P-1 A2 P where P is a permutation matrix.

Note:

A matrix whose-rows are the rows of the unit matrix but not necessarily in their natural order is called permutation matrix.

Example:

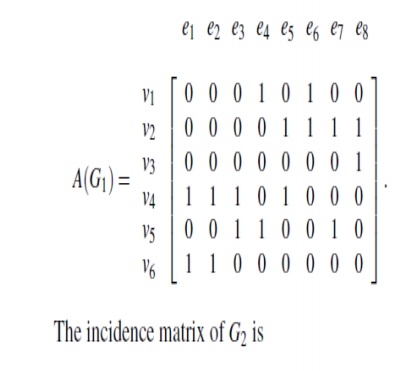
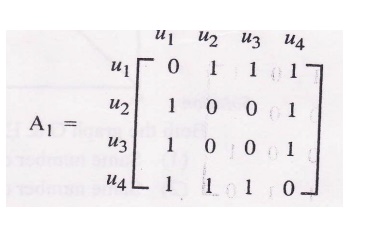
Test the Isomorphism of the graphs by considering the adjacency matrices.

Let A1 and. A2 be the adjacency matrices of G1 and G2 respectively.

Paths, Reachability and Connectedness:

DEFINTTIONS:

Path:

A Path in a graphi s a sequence v1,v to the next.ln other words,starting with the vertex v1 one can travel along edges(v1,v2),(v2,v3)..and reach the vertex vk.

Length of the path:

The number of edges appearingi n the sequence of a path is called the length of Path.

Cycle or Circuit:

A path which originates and ends in the same node is called a cycle of circuit.

A path is said to be simple if all the edges in the path are distinct. A path in which all the vertices are traversed only once is called an

elmentary Path.

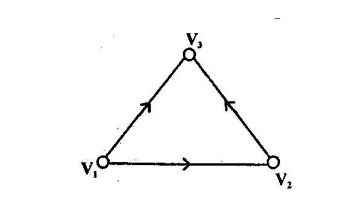
Example I :

Consider the graph:

Then some of the paths originating in node V1 and ending in node v1 are:

P1=(<V1 ,V2> ,<V2V3>)

P2=(<V1 ,V4> ,<V4 ,V3>)

P3 = (<V1 ,V2>,(V2, V4), <V4, V3>)

P4 = (<V1;V2>,<V2,V4>,<V4,V1>,<V1,V2>, <V2,V3>)

P5 = (<V1,V2>,<V2,V4>,<V4,V1 >,<V1,V4>,<V4,V3>)

P6= (<V1,Vl>, ( V1,V1), ( V1,V2), < V2, V3>)

Here,paths P1P2 and P3 are elementary path.

Path P5 is simple but not elementary.

DEFINITION:

REACHABLE:

A node v of a simple digraph is-said to ber eachable from the node u of the same graph, if there exist a path from u to v.

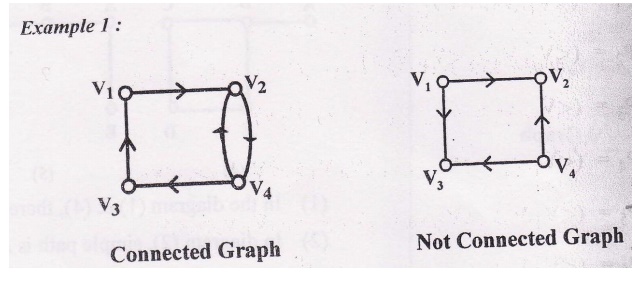
Connected Graph :

An directed graph is said to be connected if any pair of nodes are reachable from one another that is, there is a path between any pair of nodes.

A graph which is not connected is called disconnected graph.

Components of a Graph :

The connected subgraphs of a graph G are called components of the.' graph G.

DEFINITION:

Unilaterally Connected:

A simple digraph is said to be unilaterally connected if for any pair of nodes of the graph atleast one of the node of the pair is reachable from the node.

Strongly Connected:

A simple digraph is said to be strongly connected if for any pair of nodes of the graph both the nodes of the pair are reachable from the one another.

Weakly Connected:

We call a digraph is weakly.connected if it is connected.as an undirected graph in which the direction of the edges is neglected.

Note:

1.A unilateraaly connected digraph is weakly connectedbut a weakly connected digraph is not necessarily unilaterally connected.

2.A strongly connected digraph is both unilaterally and weakly connected.

EXAMPLE:

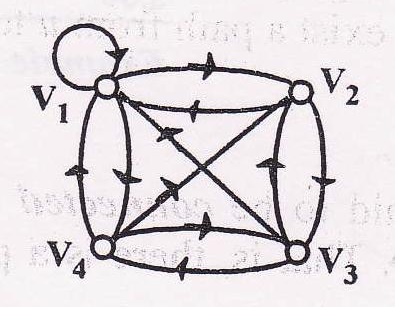
For example consider the graph:

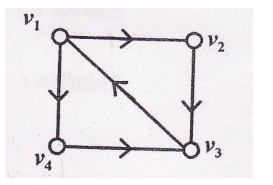
It is strongly connected graph. For,

The possible pairs of vertices of the graph are (v1 v2), (v1 v3), (v1 V4), (V2 V3) and (v2 V4)

(1)  Consider the pair (v1 v2)

Then there is a path from v1 to v2,via v1-> v2 and path from v2-> v1,via v2->v3->v1

(2) Consider the pair (v1 v3)

There is a path from v1 to v3, via v1 -> v2-> v3 and path from v3 to v1 via v3 - > v1.

similarly we can prove it for the remaining pair of vertices,each vertices is reachable from other.

Given graph is strongly connected

DEFINITION:

For a simple digraph maximal strongly connected subgraph is called strong component.

For the digraph:

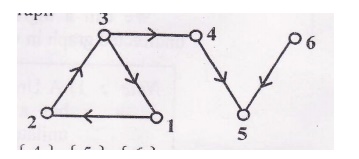
{1,2,3},{4},{5},{6} are strong component.

The possible Hamilton cycles are

(l) A-B-C-D-A

(2)  A-D-C-B-A 

(3)  B->C-D-A-B 

(4)  B-A-D-C-B 

(s) C-D-A-B-C 

(6)  C-B-A-D-C 

(7)  D-A-B-C-D 

(S) D-C-B-A-D 

(Since all the vertices appeares exactly once),but not all the edges. Since,G 1 contains Hamiltonian cycle,G 1- is a Hamiltonian graph. 

(2)  G2 contains Hamiltonian paths,namely 

(1)  A-> B-C-D 

(2)  A -> B-D-C 

D->C-B-A etc.

We cannot find Hamiltonian cycle in G2.

Therefore G2 is not a Hamiltonian graph

Properties :

(1)  A Hamiltonianc irbuitc ontainsa Hamiltonian path but a graph , Containing a Hamiltonian path need not have a Hamiltonian cycle. 

(2)  By deleting any one edge from Hamiltonian cycle,we can get Hamiltonian path. 

(3)   A graph may contain more than one Hamiltonian cycle. 

(4)   A complete graph kn, will always have a Hamiltonian cycle, when n>=3 

Note :

We don't have simple necessary and sufficient criteria for the existence of Hamiltonian cycles. However, we have many theorems that give sufficient conditions for the existence of Hamiltonian cycles.

Also, certain properties can be used to show that a graph

Has no Hamiltonian cycle.F or example a, graph with a vertex of degree one cannot have a Hamiltonian cycle, since in a Hamiltonian cycle each vertex is incident with two edges in the cycle.

4 EULER GRAPH & HAMILTON GRAPH:

Example:Explain Konisberg bridge problem.Repersent the problem by mean of graph.Does the problem have a solution?

Solution: There are two islands A and B formed by a river.They are connected to each other and to the river banks C and D by means of 7-bridges

The problem is to start from any one of the 4 land areas.A,B,C,D, walk across each bridge exactly once and return to the starting point.(without swimmimg across the river)

This problem is the famous Konisberg bridge problem.

When the situation is represented by a graph,with vertices representating the land areas the edges representing the bridges,the graph will be shown as fig:

Theorem:

In a simple digraph,G=(V,E) every node of the digraph lies in exactly one strong component.

Proof:

Let              v  €  V(G)  and  S  be  the  set  of  all  th

The problem is to find whether there is an Eulerian circuit or cycle(i.e.a circuit containing every edge exactly once) in a graph.

Here, we can not find a Eulerian circuit.Hence,Konisberg bridge problem has no solution .

EULER GRAPH:

Definition: Euler path:

A path of a graph G is called an Eulerian path,if it contains each edge of the graph exactly once.

Eulerian Circuit or Eulerian Cycle:

A circuit or cycle of a graph G is called an Eulerian circuit or cycle,if it includes each of G exactly once.

(Here starting and ending vertex are same).

An Eulerian circuit or cycle should satisfies the following conditions.

(1)Starting and ending points(vertices) or same.

(2)Cycle should contain all the edges of the graph but exactly once.

Eulerian Graph or Euler Graph:

Any graph containing an Eulerian circuit or cycle is called an Eulerian graph.

Theorem:

A connected graph is Euler graph(contains Eulerian circuit) if and only if each of its vertices is of even degree.

Proof:

Let G be any graph having Eulerian circuit(cycle) and let “C” origin(and terminus) vertex as u.Each time a vertex as an internal of C,then two of the edges incident with v are accounted for degree.

We  get,for  internal  vertex  v  €  (G)

d(v)=2+2*{number of times u occur inside V

=even degree.

Conversely, assume each of its vertices has an even degree.

Claim: G has an Eulerian circuit.Support not, i.e.,Assume G be a connected graph which is not having an Euler circuit with all vertices of even degree and less number of edges.That is ,any degree having less number of edges than G,then it has an Eulerian circuit.Since each vertex of G has degree atleast two,therefore G contains closed path.Let C be a closed path of maximum possible length in G.If C itself has all the edges of G,then C itself an Euler circuit in G.

By assumption,C is not an Euler circuit of G and G-E© has some componen |E(G’)|>0.C has less number of egdes than vertices of even degtee,thus the connected graph degree.Since |E(G’)|< |E(G)|,therefore G’ is vertex v in both C and C’. Now join’withC commen vertex v,we get CC’ is a closed pa the chioices of C.

G has an Eulerian circuit.

G is Euler graph.