Chapter: Mathematics (maths) : Discrete Mathematics : Combinatorics
Discrete Mathematics - Combinatorics
COMBINATORICS
1 MATHEMATICAL INDUCTION
2 STRONG INDUCTION & WELL ORDERING
3 RECURRENCE RELATION
4 SOLVING LINEAR RECURRENCE RELATIONS
5 GENERATING FUNCTION
6 THE PRINCIPLE OF INCLUSION & EXCLUSION
Pigeon Hole Principle:
If (n=1) pigeon occupies ‘n’ holes then atleast one hole has more than 1 pigeon.
Proof:
Assume (n+1) pigeon occupies „n‟ holes.
Claim: Atleast one hole has more than one pigeon.
Suppose not, ie. Atleast one hole has not more than one pigeon.
Therefore, each and every hole has exactly one pigeon.
Since, there are ‘n’ holes, which implies, we have totally ‘n’ pigeon.
Which is a Þ Ü to our assumption that there are (n+1) pigeon.
Therefore, atleast one hole has more than 1 pigeon.
1 MATHEMATICAL INDUCTION
EXAMPLE 1:show that






SOLUTION :
Let p(n): 12 + 32 + 52 +…… n-1)2 = - n(2n-1)(2n+1)
1.p(1): 12 = - 1(2-1)(2+1) = - . 3
=1 is true.
2.ASSUME p(k)is true.
12 + 32 + 52 +…… k-1)2 = - n(2k-1)(2k+1) -> (1) Is true.
CLAIM : p(k+1) is true.
P (k+1) = k (2k-1) (2k+1) +(2k+1)2 using (1)
= (2k+1) [k(2k-1) +3(2k+1)]
= (2k+1) (2k2+5k+3)
= (2k+1)(2k+3)(k+1)
= (k+1) [2(k+1)-1][2(k+1)+1]
P(k+1) is true .
BY THE PRINCIPLE OF MATHEMATICAL INDUCTION,
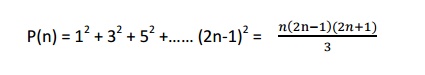
EXAMPLE 6:Use mathematical induction to show that n3 - n is divisible by 3. For n Ɛ+ )
SOLUTION:
Let p(n): nn - n is divisible by 3.
1. p(1): 13 - 1 is divisible by 3,is true.
2. ASSUME p(k): k3 - k is divisible by 3. -> (1)
CLAIM : p(k+1) is true .
P (k+1): (k+1)3 - (k+1)
= k3 +3k2 + 3k+1 - k-1
= (k3-k) + 3(k2+k) ->(2)
(1) => k3 – k Is divisible by 3 and 3(k2 + k) is divisible by 3 ,we have equation (2) is divisible by 3
Therefore P(k+1) is true.
By the principle of mathematical induction , n3 - n is divisible by 3.
2 Strong Induction
There is another form of mathematics induction that is often useful in proofs.In this form we use the basis step as before, but we use a different inductive step. We assume that p(j)is true for j=1and…,k show that p(k+1)must also be true based on this assumption . This is called strong Induction (and sometimes also known as the second principles of mathematical induction).
We summarize the two steps used to show that p(n)is true for all positive integers n.
Basis Step : The proposition P(1) is shown to be true
Inductive Step: It is shown that
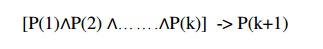
NOTE:
The two forms of mathematical induction are equivalent that is, each can be shown to be valid proof technique by assuming the other
EXAMPLE 1: Show that if n is an integer greater than 1, then n can be written as the product of primes.
SOLUTION:
Let P(n) be the proportion that n can be written as the product of primes
Basis Step : P(2) is true , since 2 can be written as the product of one prime
Inductive Step: Assume that P(j) is positive for all integer j with j<=k. To complete the Inductive Step, it must be shown that P(k+1) is trueunder the assumption.
There are two cases to consider namely
i) When (k+1) is prime
ii) When (k+1) is composite
Case 1 : If (k+1) is prime, we immediately see that P(k+1) is true.
Case 2: If ( k+1) is composite
Then it can be written as the product of two positive integers a and b with 2<=a<b<=k+1. By the Innduction hypothesis, both a and b can be written as the product of primes, namely those primes in the factorization of a and those in the factorization of b .
The Well-Ordering Property:
The validity of mathematical induction follows from the following fundamental axioms about the set of integers.
Every non-empty set of non negative integers has a least element.
The well-ordering property can often be used directly in the proof.
Problem :
What is wrong with this “Proof” by strong induction ?
Theorem :
For every non negative integer n, 5n = 0
Proof:
Basis Step: 5 – 0 = 0
Inductive Step: Suppose that 5j = 0 for all non negative integers j with o<=j<=k. Write k+1 = i+j where I and j are natural numbers less than k+1. By the induction hypothesis
5(k+1) = 5(i+j) = 5i + 5j = 0+ 0 =0
Example 1:
Among any group of 367 people, there must be atleast 2 with same birthday, because there are only 366 possible birthdays.
Example 2:
In any group of 27 English words, there must be at least two, that begins with the same letter, since there are only 26 letters in English alphabet
Example 3:
Show that among 100 people , at least 9 of them were born in the same month
Solution :
Here, No of Pigeon = m = No of People = 100
No of Holes = n = No of Month = 12
Then by generalized pigeon hole principle
{[100-1]/12}+1 = 9, were born in the same month
Combinations:
Each of the difference groups of sections which can be made by taking some or all of a number of things at a time is called a combinations.
The number of combinations of ‘n’ things taken ‘r’ as a time means the number as groups of ‘r’ things which can be formed from the ‘n’ things.
It denoted by nCr.
The value of nCr :
Each combination consists /r/ difference things which can be arranged among themselves in r! Ways. Hence the number of arrangement for all the combination is nCr x r! . This is equal to the permulations of ‘n’ difference things taken ‘r’ as a time.
nCr x r! =n P r
nCr = n P r / r! -------------------- à(A)
= n (n-1) , (n-2)........ (n-r+1) / 1,2,3,.......r
Cor 1 : nPr = n! / (n-r)! -------- à(B)
Substituting (B) in (A) we get
nCr = n! / (n-r)!r!
Cor 2: To prove that nCr = nCn-r
Proof :
nCr = n! / r!(n-r)! --------------------- à(1)
nCn-r = n! / (n-r)! [n-(n-r)]!
= n! / (n-r) ! r! -------------------------- à(2)
From 1 and 2 we get
nCr=nCn-r
Example :
30C28 = 30 C30 – 28
=30 C2
30 x 29 / 1x2
Example 2:
In how many can 5 persons be selected from amongs 10 persons ?
Sol :
The selection can be done in 10C5 ways.
=10x9x8x7x6 / 1x2x3x4x5
= 9 x 28 ways.
Example 5 :
How many ways are there to from a commitiee , if the consists of 3 educanalis and 4 socialist if there are 9 educanalists and 11 socialists.
Sol : The 3 educanalist can be choosen from a educanalist in 9C3 ways. The 4 socialist can be choosen from 11 socialist in 11C4 ways.
.`. By products rule , the number of ways to select the commitiee is
=9C3.11C4
= 9! / 3! 6! . 11! / 4! 7!
= 84 x 330
27720 ways.
Example 6 :
1. A team of 11 players is so be chosen from 15 members. In how ways can this be done if
i. One particular player is always included.
ii. Two such player have always to be included.
Sol : Let one player be fixed the remaining players are 14 . Out of these 14 players we have to select 10 players in 14C10 ways.
14C4 ways. [.`. nCr = nCn-r ]
14x13x12x11 / 1x2x3x4
1001 ways.
2. Let 2 players be fixed. The remaining players are 13. Out of these players we have to select a players in 13C9 ways.
13C4 ways [ .`. nCr = nCn-r ]
13x12x11x10 / 1x2x3x4 ways
715 ways.
Example 9 :
Find the value of ‘r’ ifr= 20Cr-
Sol : Given 20 Cr = 20C20-(r-2) -- -- > r=20-(r+2) ---------------- à(1)
(1) -----à r=20 - r – 2
2r = 18
r = 9
Example 12 :
From a commitiee consisting of 6 men and 7 women in how many ways can be select a committee of
(1) 3men and 4 women.
(2) 4 members which has atleast one women.
(3) 4 persons of both sexes.
(4) 4 person in which Mr. And Mrs kannan is not included.
Sol :
(a) 3 men can be selected from 6 men is 6C3 ways. 4 women can be selected from 7 women in 7C4 ways.
.`. By product rule the committee of 3 men and 4 women can be selected in
6C3 X 7C4 ways = 700 ways.
(b) For the committee of atleast one women we have the following possibilities
1. 1 women and 3 men
2. 2 women and 2 men
3. 3 women and 1 men
4 women and 0 men
There fore the selection can be done in
= 7C1 x 6C3 + 7C2 x 6C2 + 7C3 x6C1 + 7C4 x 6C6 ways
= 7x20+21x15+35x6+35x1
=140x315x210x35
=700 ways.
(d) For the committee of bath sexes we have the following possibilities .
1. 1 men and 3 women
2. 2 men and 2 women
3. 3 men and 1 women
Which can be done in
=6C1x7C3+6C2x7C2+6C3x7C1
=6x35+15x21+20x7
=210+315+140
=665 ways.
Sol : (1) 4 balls of any colour can be chosen from 11 balls (6+5) in 11C4 ways.
=330 ways.
(2) The 2 white balls can be chosen in 6C2 ways. The 2 red balls can be chosen in 5C2 ways. Number of ways selecting 4 balls 2 must be red.
=6C2 + 5C2
=15 + 10
=25 ways.
Number of ways selecting 4 balls and all Of same colour is = 6C4 + 5C4
=15+5
=20ways.
DEFINITION
.
A Linear homogeneous recurrence relation of degree K with constant coefficients is a recurrence relation of the form
The recurrence relation in the definition is linesr since the right hand side is the sum of multiplies of the previous terms of sequence.
The recurrence relation is homogeneous , since no terms occur that are ot ultiplies of the aj s.
The coefficients of the terms of the sequence are all constants ,rather tha fu tio that depe ds o .
The degree is k because an is exrressed in terms of the previous k terms of the sequence
Ex:4 The recurrence relation
Hn =2Hn-1+1
Is not homogenous
Ex: 5 The recurrence relation
Bn =nBn-1
Does not have constant coefficient Ex:6 The relation T(k)=2[T(k-1)]2KT(K-3) Is a third order recurrence relation & T(0),T(1),T(2) are the initial conditions.
Ex:7 The recurrence relation for the function
f : N->Z defined by
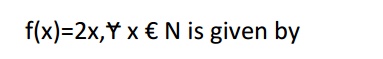
f(n+1)=f(n)+2,n>=0 with f(0)=0
f(1)=f(0)+2=0+2=2
f(2)=f(1)+2=2+2=4 and so on.
It is a first order recurrence relation.
3 Recurrence relations.
Definition
An equation that expresses an, the general term of the sequence {an} in terms of one or more of the previous terms of the sequence , namely a0,a1,.....,an-1 ,for all integers n with n>=0,where n0 is a non –ve integer is called a recurrence relation for {an} or a difference equation.
If the terms of a recurrence relation satisfies a recurrence relation , then the sequence is called a solution of the recurrence relation.
For example ,we consider the famous Fibonacci sequence
0,1,1,2,3,5,8,13,21,.....,
which can be represented by the recurrence relation.
Fn=Fn-1+Fn-2,n>=2
F0=0,F1=1. Here F0=0 & F1=1 are called initial conditions. It is a second order recurrence relation.
4 Solving Linear Homogenous Recurrence Relations with Constants Coefficients.
Step 1: Write down the characteristics equation of the given recurrence relation .Here ,the degree of character equation is 1 less than the number of terms in recurrence relations.
Step 2: By solving the characteristics equation first out the characteristics roots.
Step 3: Depends upon the nature of roots ,find out the solution an as follows:
Case 1: Let the roots be real and distinct say r1,r2,r3.....,rn then
An= α1r1n+ α2r2n+ α3r3n+........+ αnrnn,
Where α1, α2, ....,αn are arbitrary constants.
Case 2: Let the roots be real and equal say r1=r2=r3=rn then
An= α1r1n+ nα2r2n+n2 α3r3n+........+n2 αnrnn, Where α1, α2, ....,αn are arbitrary constants.
Case 3: When the roots are complex conjugate, then an=rn(α1cosn + α2sinn )
Case 4: Apply initial conditions and find out arbitrary constants.
Note:
There is no single method or technique to solve all recurrence relations. There exist some recurrence relations which cannot be solved. The recurrence relation.
S(k)=2[S(k-1)]2-kS(k-3) cannot be solved.
Example 1: If sequence an=3.2n,n>=1, then find the recurrence relation.
Solution:
For n>=1
an=3.2n,
now, an-1=3.2n-1,
=3.2n / 2
an-1=an/2
an = 2(an-1)
an = 2an-1, for n> 1 with an=3
Example 2 :
Find the recurrence relation for S(n) = 6(-5),n> 0
Sol :
Given S(n) = 6(-5)n
S(n-1) = 6(-5)n-1
=6(-5)n / -5
S(n-1) = S(n) / -5
Sn = -5.5 (n-1) , n> 0 with s(0) =6
Example 5: Find the relation from Yk =A.2k + B.3k
Sol :
Given Yk =A.2k + B.3k -------------- à(1)
Yk+1 =A.2k+1 + B.3k+1
=A.2k .2 + B3k .3
Yk+1 =2A.2k + 3B.3k
Yk+2 =4A.2k + 9B.3k ------------------------ à(3)
(3) – 5(2) + 6(1)
yk+2 -5yk+1 + 6yk =4A.2k + 9B.3k -10A.2k - 15B.3k + 6A.2k + 6B.3k
=0
.`. Yk+1-5yk+1 + 6yk = 0 in the required recurrence relation.
Example 9 :
Solve the recurrence relation defind by So = 100 and Sk (1.08) Sk-1 for k> 1
Sol ;
Given S0 = 100
Sk = (1.08) Sk-1 , k> 1
S1 = (1.08) S0 = (1.08)100
S2 = (1.08) S1 = (1.08)(1.08)100
=(1.08)2 100 S3 = (1.08) S2 = (1.08)(1.08)2100
Example 15 : Find an explicit formula for the Fibonacci sequence .
Sol ;
Fibonacci sequence 0,1,2,3,4........ satisify the recurrence relation fn= fn-1 + fn-2
fn- fn-1 - fn-2 = 0
& also satisfies the initial condition f0=0,f1=1 Now , the characteristic equation is
r2-r-1 =0 Solving we get r=1+ 1+4 / 2
= 1+ 5 / 2
Sol :
fn = 1α (1+ 5 / 2)n + α2 (1- 5 / 2)n
(A) given f0 =0 put n=0 in (A) we get
f = 1α (1+ 5 / 2)0 + α2 (1- 5 / 2)0
(A) -- > α +α =0 ------------------------à(1)
given f1 =1 put n=1 in (A) we get
f1 = α1 (1+ 5 / 2)1 + α2 (1- 5 / 2)1
(A)è(1+ 5 / 2)n + α2 (1- 5 / 2)n α2 = 1 -------à(2)
Substituting these values in (A) we get
Solution fn=1/5 (1+5/ 2 )n -1/5 (1+5/ 2 )n
Example 13 ;
Solve the recurrence equation an = 2an-1 – 2an-2 , n> 2 & a0 =1 & a1=2
Sol :
The recurrence relation can be written as an - 2an-1 + 2an-2 = 0
The characteristic equation is r2 – 2r -2 =0
Roots are r= 2+ 2i / 2 =1+ i
LINEAR NON HOMOGENEOUS RECRRENCE RELATIONS WITH CONSTANT COEFFICIENTS
A recurrence relation of the form
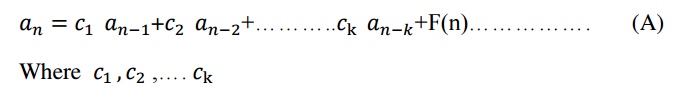
are real numbers and F(n) is a function not identically zero depending only on n,is called a non-homogeneous recurrence relation with constant coefficient.
Here ,the recurrence relation
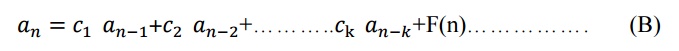
Is called Associated homogeneous recurrence relation.
NOTE:
(B) is obtained from (A) by omitting F(n) for example ,the recurrence relation 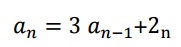 is an example of non-homogeneous recurrence relation .Its associated
is an example of non-homogeneous recurrence relation .Its associated
Homogeneous linear equation is
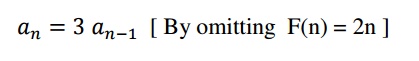
[ By omitting F(n) = 2n ]
PROCEDURE TO SOLVE NON-HOMOGENEOUS RECURRENCE RELATIONS:
The solution of non-homogeneous recurrence relations is the sum of two solutions.
1.solution of Associated homogeneous recurrence relation (By considering RHS=0).
2.Particular solution depending on the RHS of the given recurrence relation
STEP1:
a) if the RHS of the recurrence relation is

LHS of the given recurrence relation
(b) if the RHS is a n then we have
Case1:if the base a of the RHS is the characteristric root,then the solution is of the cann .therefore substitute can in place of ,can-1 in place of c(n-1) an-1 etc..
Case2: if the base a of RHS is not a root , then solution is of the form can therefore substitute can in place of an , can-1 in place of an-1 etc..
STEP2:
At the end of step-1, we get a polynomial in ‘n’ with coefficient c0,c1……on LHS
Now, equating the LHS and compare the coefficients find the constants c0,c1,….
Example 1:

It’s characteristic equation is
r-3=0 => r=3
now, the solution of associated homogeneous equation is
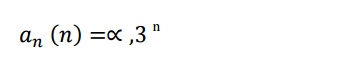
To find particular solution
Since F(n) =2n is a polynomial of degree one,then the solution is of the from d (say) where c and d are constant
Now, the equation

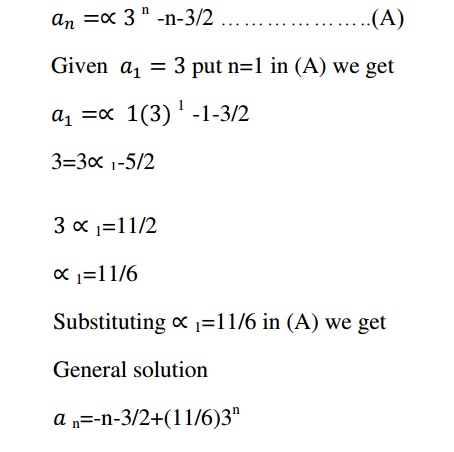
Example:2
Solve s(k)-5s(k-1)+6s(k-2)=2
With s(0)=1 ,s(1)=-1
Solution:
Given non-homogeneous equation can be written as

To find particular solution
As RHS of the recurrence relation is constant ,the solution is of the form C , where C is a constant
Therefore the equation
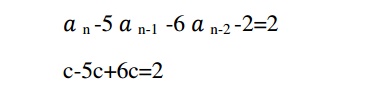
2c=2
c=2
the particular solution is sn(p)=1
the general solution is sn= sn(n)+ sn(p)
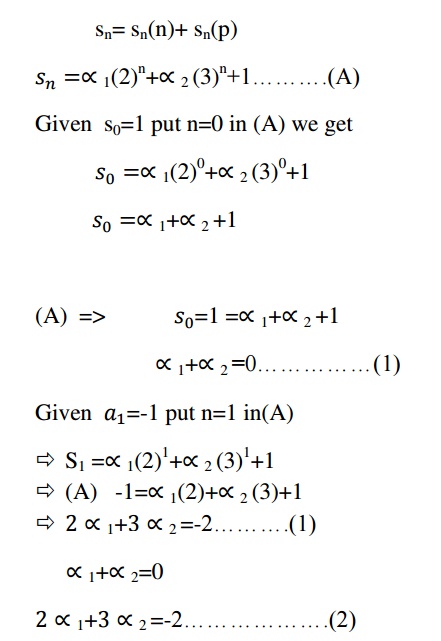



Example:
HOW MANY INTEGERS BETWEEN 1 to 100 that are
i) not divisible by 7,11,or 13
ii) divisible by 3 but not by 7 Solution:
i) let A,B and C denote respectively the number of integer between 1 to 100 that are divisible by 7,11 and 13 respectively
now,
|A| =[100/7]=14 |B| =[100/11]=9 |C| =[100/13]=7 |A^B| =[100/7]=1
|A^C| =[100/7*13]=1 |B^C| =[100/11*13]=0
|A^B^C| =[100/7*11*13]=0 That are divisible by 7, 11 or 13 is |AvBvC| By principle of inclusion and exclusion
|AvBvC| =|A|+|B|+|C|-|A^B|-|A^C|-|B^C|+|A^B^C|
=14+9+7-(1+1+0)+0 =30-2=28
Now,
The number of integer not divisible by any of 7,11,and 13=total-|AvBvC| =100-28=72
ii) let A and B denote the no. between 1 to 100 that are divisible by 3 and 7 respectively
|A| =[100/3]=33 |B|=[100/7]=14
| A^B |=[100/3*7]=14
The number of integer divisible by 3 but not by 7 =|A|-| A^B |
=33-4=29
Example:
There are 2500 student in a college of these 1700 have taken a course in C, 1000 have taken a course pascal and 550 have taken course in networking .further 750 have taken course in both C and pascal ,400 have taken courses in both C and Networking and 275 have taken courses in both pascal and networking. If 200 of these student have taken course in C pascal and Networking.
i)how many these 2500 students have taken a courses in any of these three courses C ,pascal and networking?
ii)How many of these 2500 students have not taken a courses in any of these three courses C,pascal and networking?
Solution:
Let A,B and C denotes student have taken a course in C,pascal and networking respectively
Given
|A|=1700
|B|=1000
|C|=550
| A^B | =750 | A^C|=40
| B^C =275
| A^B^C |=200
Number of student who have taken any one of these course=| A^B^C | By principle of inclusion and exclusion
|AvBvC| =|A|+|B|+|C|-|A^B|-|A^C|-|B^C|+|A^B^C|
=(1700+1000+550)-(750+400+275)+200
=3450-1425
=2025
The number between 1-100 that are divisible by 7 but not divisible by 2,3,5,7=
=|D|- | A^B^C ^CD|
=142-4=138
Example:
A survey of 500 television watches produced the following information.285 watch hockey games.195 watch football games 115 watch basketball games .70 watch football and hockey games.50 watch hockey and basketball games and 30 watch football and hockey games.how many people watch exactly one of the three games?
Solution:
H=> let television watches who watch hockey
F=> let television watches who watch football
B=> let television watches who watch basketball
Given
n(H)=285,n(F)=195,n(B)=115,n(H^F)=70,n(H^B),n(F^B)=30
let x be the number television watches who watch all three games now, we have
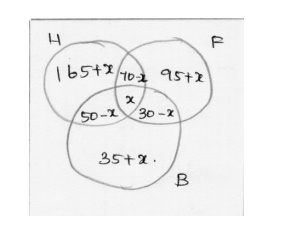
Given 50 members does not watch any of the three games. Hence (165+x)+(95+x)+(35+x)+(70+x)+(50+x)+(30+x)+x=500
=445+x=500
X=55
Number of students who watches exactly one game is=165+x+95+x+35+x =295+3*55 =460
5 .Generating function:
The generating function for the sequence ‘S’ with terms a0,a1,…..
an of real numbers is the infinite sum.
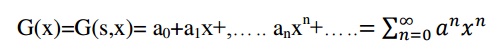
For example,
i) the generating function for the sequence ‘S’ with the terms 1,1,1,1…..i given by,
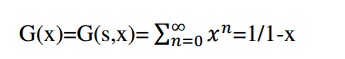
G(x)=G(s,x)= 1/1-x
ii)the generation function for the sequence ‘S’ with terms 1,2,3,4…..is
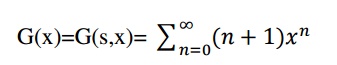
=1+2x+3x2+……..
=(1-x)-2=1/(1-x)2
2.Solution of recurrence relation using generating function
Procedure:
Step1:rewrite the given recurrence relation as an equation with 0 as RHS
Step2:multiply the equation obtained in step(1) by xn and summing if form 1 to ∞
Step3:put G(x)= 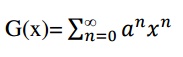 and write G(x) as a function of x
and write G(x) as a function of x
Step 4:decompose G(x) into partial fraction
Step5:express G(x) as a sum of familiar series
Step6:Express an as the coefficient of xn in G(x)
The following table represent some sequence and their generating functions



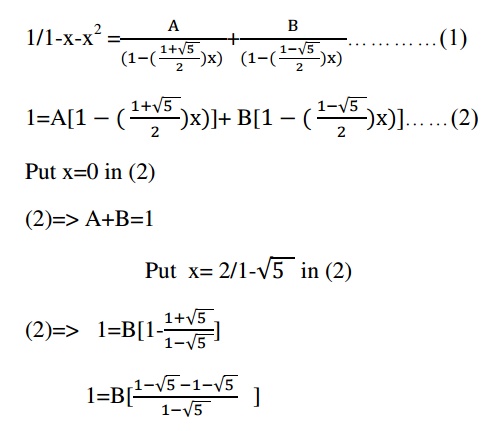

6THE PRINCIPLE OF INCLUSION –EXCLUSION
Assume two tasksT1 and T2 that can be done at the same time(simultaneously) now to find the number of ways to do one of the two tasks T1and T2, if we add number ways to do each task then it leads to an over count. since the ways to do both tasks are counted twice. To correctly count the number of ways to do each of the two tasks and then number of ways to do both tasks
i.e ^(T1vT2)=^( T1)+^( T2)-^( T1^T2)
this technique is called the principle of Inclusion –exclusion
FORMULA:4
1) | A1vA2vA 3|=|A1|+|A2|+|A3|-|A1^A2|-|A1^A3|-|A2^A3|+|A1^A2^ A3|
2) |A1vA2vA 3v A 4|=|A1|+|A2|+|A3|+| A4 |-|A1^A2|-|A1^A3|-|A1^A4|-|A2^A3|-
|A2^A4|-|A3^A4|+|A1^A2^ A3 |+|A1^A2^ A4 |+|A1^A3^ A4 |+|A2^A3^ A4 |+|A1^A2^ A3^A4 |
Example1:
A survey of 500 from a school produced the following information.200 play volleyball,120 play hockey,60 play both volleyball and hockey. How many are not playing either volleyball or hockey?
Solution:
Let A denote the students who volleyball
Let B denote the students who play hockey
It is given that
n=500
|A|=200
|B|=120
|A^B|=60
Bt the principle of inclusion-exclusion, the number of students playing either volleyball or hockey
|AvB|=|A|+|B|-|A^B|
|AvB|=200+120-60=260
The number of students not playing either volleyball or hockey=500-260
=240
Example2:
In a survey of 100 students it was found that 30 studied mathematics,54 studied statistics,25 studied operation research,1 studied all the three subjects.20 studied mathematics and statistic,3 studied mathematics and operation research And 15 studied statistics and operation research
1.how many students studied none of these subjects?
2.how many students studied only mathematics?
Solution:
1) Let A denote the students who studied mathematics Let B denote the students who studied statistics
Let C denote the student who studied operation research
Thus |A|=30 ,|B|=54 ,|C|=25 ,|A^B|=20 ,|A^C|=3 ,|B^C|=15 ,and |A^B^C|=1
By the principle of inclusion-exclusion students who studied any one of the subject is
|AvBvC|=|A|+|B|+|C|=|A^B|-|A^C|-|B^C|+|A^B^C|
=30+54+25-20-3-15+1
=110-38=72
Students who studied none of these 3 subjects=100-72=28 2) now ,
The number of students studied only mathematics and statistics=n(A^B)-n(A^B^C)
=20-1=19
The number of students studied only mathematics and operation research=n(A^C)-n(A^B^C)
=3-1=2
Then The number of students studied only mathematics =30-19-2=9
Example3:
How many positive integers not exceeding 1000 are divisible by 7 or 11? Solution:
Let A denote the set of positive integers not exceeding 1000 are divisible by
7
Let B denote the set of positive integers not exceeding 1000 that are divisible by 11
Then |A|=[1000/7]=[142.8]=142 |B|=[1000/11]=[90.9]=90 |A^B|=[1000/7*11]=[12.9]=12
The number of positive integers not exceeding 1000 that are divisible either 7 or 11 is |AvB|
By the principle of inclusion
exclusion |AvB|=|A|+|B|-|A^B|
=142+90-12=220
There are 220 positive integers not exceeding 1000 divisible by either 7 or
11
Example:
A survey among 100 students shows that of the three ice cream flavours vanilla,chocolate,and strawberry ,50 students like vanilla,43 like chocalate ,28 like strawberry,13 like vanilla, and chocolate,11like chocalets and strawberry,12 like strawberry and vanilla and 5 like all of them.
Find the number of students surveyed who like each of the following flavours
1.chocalate but not strawberry
2.chocalate and strawberry ,but not vanilla
3.vanilla or chocolate, but not strawberry
Solution:
Let A denote the set of students who like vanilla
Let B denote the set of students who like chocalate
Let C denote the set of students who like strawberry
Since 5 students like all flavours
|A^B^C|=5
12 students like both strawberry and vanilla
|A^C|=12
But 5 of them like chocolate also, therefore
|A^C-B|=7
Similarly |B^C-A|=6
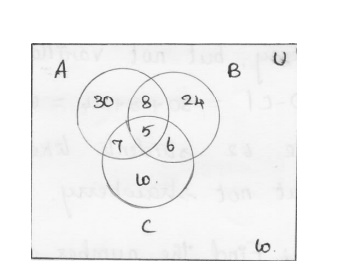
Of the 28 students who like strawberry we have already accounted for
7+5+6=18
So, the remaining 10 students belong to the set C-|AvB| similarly
|A-BvC|=30 and |B-AvC|=24
Thus for we have accounted for 90 of the 100 students the remaining 10 students like outside the region AvBvC
Now,
1.|B-C|=24+8=32
So 32 students like chocolate but not strawberry
2.|B^C-A|=6
Therefore 6 students like both chocolate and strawberry but not vanilla
3.|AvB-C|=30+8+24=62
Therefore 62 students like vanilla or chocolate but not strawberry
Example 5: find the number of integers between 1 to 250 that are not divisible by any of the integers 2,3,5 and 7
Solution:
Let A denote the integer from 1 to 250 that are divisible by 2
Let B denote the integer from 1 to 250 that are divisible by 3 Let C denote the integer from 1 to 250 that are divisible by 5 Let D denote the integer from 1 to 250 that are divisible by 7
|A|=[250/2]=125
|B|=[250/3]=83
|C|=[250/5]=50
|D|=[250/7]=35
Now, the number of integer between 1-250 that are divisible by 2 and 3=|A^B|=[250/2*3]=41
The number of integer divisible by 2 and 5=|A^C|=[250/2*5]=25 Similarly
|A^D|=[250/2*7]=17
|B^C|=[250/3*5]=16
|B^D|=[250/3*7]=11 |C^D| =[250/5*7]=7
The number of integer divisible by 2,3,5=|A^B^C|=[250/2*3*5]=8.
1. Solve the recurrence relation an+2- an+1-6 an=0 given a0=2 and a1=1 using generating functions
SOLUTION:
Given recurrence relation is
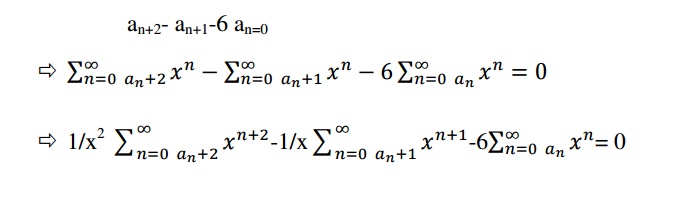

2-x = A(1+2x) + B(1-3x)……(1)
Put x = -1/2 in (1) we get
5/2 = 5/2B => B = 1
Put x = 1/3 in (1) we get A = 1

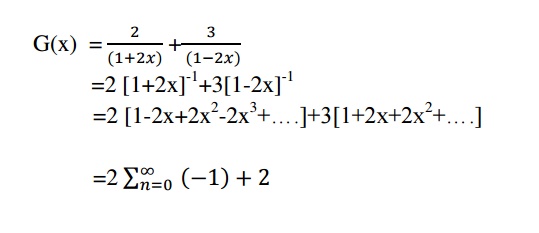
Related Topics