Important Short Objective Question and Answers: Logic and Proofs

LOGIC AND PROOFS

1. Without constructing the truth table show that  p→   (q→ p)≡￢ p(p→   q)

Solution

p→   (q→ p)≡p→￢(q∨p)

≡￢p∨(￢q ∨p)

≡￢p∨(p∨￢q)

≡   (￢p∨p)∨￢q

≡      T∨￢q

≡           T.

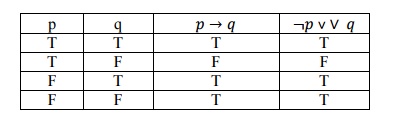
2. Prove that p→   q   is   logically   prove   that (￢p∨q)

Solution:

p       q        →      ¬  ˅∨

T       T       T       T

T       F       F       F

F       T       T       T

F       F       T       T

3. Define a tautology. With an example.

A statement that is true for all possible values of its propositional variables is called a tautology universely valid formula or a logical truth.

Example:  p ∨￢q is a tautology.

4. When do you say that two compound statement proposition are equivalent.

Two compound proposition are said to be equivalent if then the have identical truth tables. 

5.     Give an indirect proof of the theorem if 3n+2 is odd, then n is odd.

Solution:

P: 3n+2 is odd

n is odd

Hypothesis: Assume that → q is false. Assume that q is false.

i.e,  n is not odd ⇒  n is even.

Analysis: If n is even then n=2k for some integer k. 3n+2= 3(2k)+2.

=   6k+2.

=   2(3k+1)

6.Define a universal specification.

(x)A(x) ⇒A(y)

If a statement of the form (x)A(x) is assumed to be true , then the universal quantifier can be dropped to obtain A(y) is true for any arbitrary object y in the universe.

7.Show that {∨,∧} is not functionally complete.

Solution: ¬ p cannot be expressed using the connectives {∨,∧} .since no sets contribution of the statement exists {∨,∧} as input if T and the output is F.

 8. Write the converse, inverse, contra positive of „If you work hard then you will be rewarded‟

Solution:

 p: you will be work hard.

 q: you will be rewarded.

¬p: You will not be work hard.

 ¬ q: You will no tbe rewarded.

 Converse: q→ p, If you will be rewarded then you will be work hard

 Contrapositive: ¬ q→ p,if You will not be rewarded then You will not be work hard.

 Inverse: ¬ p→ ¬ q, if You will not be work hard then You will no tbe rewarded.

9. let E={ -1, 0,1,2 denote a universe of discourse . If P(x ,y) : x +y =1 find the truth value of 

12.Write an equivalent formula for p∧(q « r) which contains neither the bionditional nor    conditional.

Solution :

p∧(q « r) ⇔ (  ∧(q →r) ∧(r → )

⇔ (  ∧(¬q ∨r) ∧(¬r ∨ ).

13.    Show that (x) (H(x) →M(x)) ∧  𝐇 𝐬 ⇒ 𝑴(𝒔)

15. Symbolise: For every x, these exixts a y such that x²+y² ≥   100

Solution :

( "x ) ( ∃ ) (x²+y² ≥   100)

 PART – B

1. a) Prove that 𝑷 → 𝑸 ˄ 𝑸 → 𝑹 → 𝑷 → 𝑹

Proof:

Let S: 𝑃 → 𝑄 ˄ 𝑄 → 𝑅 → 𝑃 → 𝑅

To prove: S is a tautology

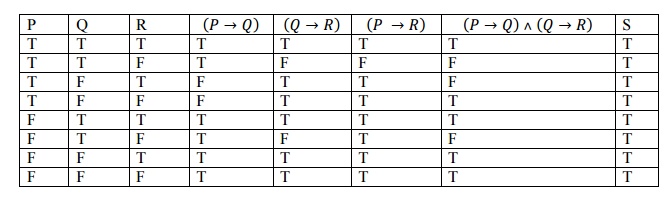
The last column shows that S is a tautology

2. Show that ￢(p↔q)≡(p∨q) ∧￢(p∧q) without constructing the truth table

Solution :

￢(p↔q)≡(p∨q) ∧￢(p∧q)

￢(p↔q)≡￢(p→q) ∧ (q→p)

≡￢(￢p∨q) ∧ (￢q∨p)

≡￢(￢p∨q) ∧￢q) ∨((￢p∨q) ∧p)

≡￢(￢p∧￢q) ∨(q∧￢q ) ∨((￢p∧p) ∨(q∧p)

≡￢(￢p∨q) ∨F∨F∨(q∧p)

≡￢(￢p∨q) ∨(q∧p)

≡(p∨q) ∧ (q∧p).

3. Obtain PCNF of (￢p→  r)∧(q↔   p).   and   hence   obtain   its   PD

Solution:

PCNF:

S⇔  ￢p → r ∧ q ↔ p .

⇔ (￢p→  ∧r)((q→p). ∧ p →q

⇔ (p∨r) ∧((￢q∨p). ∧ ￢p ∨q

⇔ ((p∨r) ∨F) ∧((￢q∨p).∨F) ∧( ￢p ∨q ∨F)

⇔ ( p ∨ r ∨ q ∧￢q )∧((￢q∨p).∨ r ∧￢ r ) ∧( ￢p ∨q ∨ p ∧￢p ) .

⇔ ( p ∨ r ∨ q ∧p ∨ r ∨￢ q) ∧((￢q∨p∨ r) ∧.(￢q ∨ p ∨￢ r) ∧( ￢p ∨q ∨r ∨(￢p ∨ q ∨￢r)

⇔ ( p ∨ r ∨ q ∧((￢q∨p∨ r) ∧.(￢q ∨ p ∨￢ r) ∧( ￢p ∨q ∨r ∨(￢p ∨q ∨￢r)

PCNF of S: ( p ∨ r ∨ q ∧((￢q∨ p∨ r) ∧.(￢q ∨ p ∨￢ r) ∧( ￢p ∨q ∨r ∨(￢p ∨q ∨￢r)

PCNF of ￢S: (p∨q∨r) ∧ ￢p ∨￢q ∨r       ∧ ￢p ∨￢q ∨￢r

PDNF of S: (p∧q∧r) ∨ ￢p ∧￢q ∧r ∨ ￢p ∨∧￢q ∧￢r .

Since  p²  is  an even integer, p is an even integer.

\ p= 2m for some integer m.

\  (2m)²  =2q² Þ q²  =2m²

Since q ²  is  an even integer, q is an even integer.

\ q= 2k f or some integer k.

Thus p & q are even . Hence they have a common factor 2. Which is a contradiction to our assumption.

Rt(2)  is irrational.

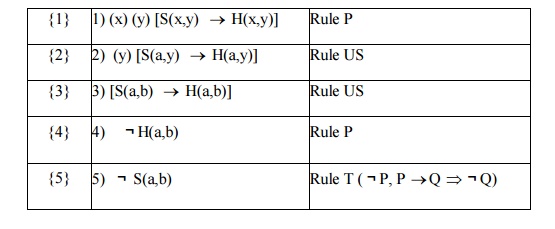
5. Verify that validating of the following inference. If one person is more successful than another, then he has worked harder to deserve success. Ram has not worked harder than Siva. Therefore, Ram is not more successful than Siva.

Solution:

Let the universe consists of all persons.

Let S(x,y): x is more successful than y.

H(x,y): x has worked harder than y to deserve success.

a: Ram

b: Siva

Then, given set of premises are

1)    (x) (y) [S(x,y) ®H(x,y)]

2)    ￢H(a,b)

3)    Conslution is ￢S(a,b).