Direct Proportion

Direct Proportion

For example, if the cost of a shirt is ₹ 500, then the price of 3 shirts will be ₹ 1,500. The price of the shirts increases as the number of shirts increases. Proceeding the same way we can find the cost of any number of such shirts.

When observing the above situation, two quantities namely the number of shirts and their prices are related to each other. When the number of shirts increases, the price also increases in such a way that their ratio remains constant.

Let us denote the number of shirts as x and the price of shirts as y rupees. Now observe the following table

From the table, we can observe that when the values of x increases the corresponding values of y also increases in such way that the ratio x/y in each case has the same value which is a constant (say k). Now let us find the ratio for each of the value from the table.

  x/y = 1/500 = 2/1000 = 3/1500 = 6/3000 = 7/3500 and so on. All the ratios are equivalent and its simplified form is 1/500.

In general, x/y = 1/500 = k (k is a constant)

When x and y are in direct proportion, we get x/y = k or x = ky  (k is a constant)

Considering any two ratios given above, say, 2/1000 = 6/3000, where 2(x₁) and 6 (x₂) are the number of shirts (x) and 1000 (y₁) and 3000 (y₂) are their prices (y). So, when x and y are in direct proportion we can write x₁/y₁ = x₂/y₂  [where, y_1,  y₂ are values of y corresponding to the values x₁, x₁ of x].

Think

The number of chocolates to be distributed to the number of children. Is this statement in direct proportion?

Try this

Observe the following 5 squares of different sides given in the graph sheet

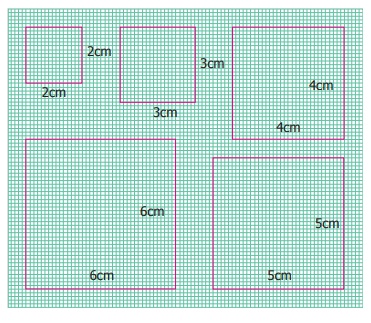
The measures of the sides are recorded in the table given below. Find the corresponding perimeter and the ratios of each of these with the sides given and complete the table.

From the information so obtained state whether the side of a square is in direct proportion to the perimeter of the square

Think

When a fixed amount is deposited for a fixed rate of interest, the simple interest changes propotionaly with the number of years it is being deposited. Can you find any other examples of such kind.

Example 4.1

If 6 children shared 24 pencils equally, then how many pencils are required for 18 children?

Solution

Let x be the number of pencils required for 18 children. As the number of children increases, number of pencils also increases.

In the case of direct proportion we take

Hence, 72 pencils are required for 18 children.

Example 4.2

If 15 chart papers together weigh 50 grams, how many of the same type will be there in a pack of 2 1/2 kilogram?

Solution

Let x be the required number of charts.

As weight increases, the number of charts also increases. So the quantities are in direct proportion.

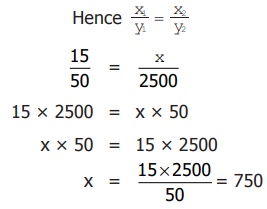
Therefore, 750 charts will weigh 2 ½ kilogram.

Unitary Method

We know the concept of unitary method studied in the previous class.

First, the value of one unit will be found. It will be useful to find the value of the required number of units. We will try to solve more problems using unitary method.

Example 4.3

Anbu bought 2 notebooks for ₹ 24. How much money will be needed to buy 9 such notebooks?

Solution

Using unitary method we can solve this as follows:

The cost of 2 notebooks = ₹ 24

The cost of 1 notebook = 24/2 =₹12

Therefore, the cost of 9 notebooks = 9×₹12

= ₹ 108

Hence, Anbu has to pay ₹108 for 9 notebooks.

Example 4.4

A car travels 90km in 2hours 30minutes. How much time is required to cover 210km?

Solution

1 hour = 60 minutes

2 hour = 120 minutes

Time taken to cover 90 km = 2hrs 30mins

= 150 minutes

Time taken to cover 1 km = 150/90 minutes.

Time taken to cover 210 km = 150/90 × 210 minutes

  = 350 minutes

= 5 hours 50 minutes

Thus, the time taken to travel 210 km is 5 hours 50 minutes