Digital-to-Analog Conversion and Analog-to-Digital Conversion

       ANALOG  TO DIGITAL  CONVERSION

Continuous analog signals from the process must be converted into digital values to be used by the computer. and digital data generated by the computer must be converted to analog signals to be used by analog actuators. We discuss analogladigital conversion in this section and digitaltoanalog conversion in the following section

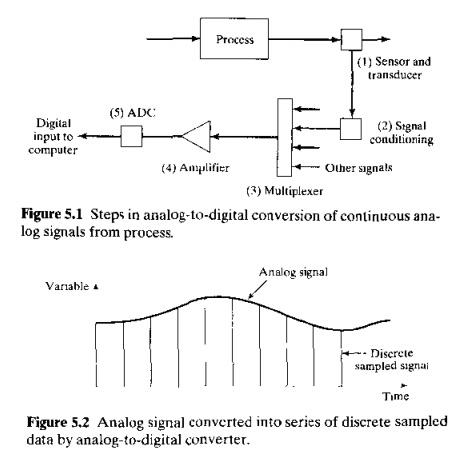
Tile procedure for converting an anaJogsignal from the process into digital fonn typically consists of the following steps and hardware devices, as illustrated in Figure 5.1:

   Sensor and transducer. This is the measuring device that generates the analog signal (SectionS.1)

    Signal conditioning.  The continuous   analog  signal from  the transducer   may require

conditioning to render it into more suitable form. Common signal conditioning steps include: (1) filtering to remove random noise and (2) conversion from one signal form to another, for example, converting a current into a voltage.

    Multiplexer. The multiplexer is a switching device connected in series with each input channel from the process; it is used to timeshare the analogtodigital converter (ADC) among the input channels. The alternative is to have a separate ADC for each input channel. which would he costly for a large application with many input channels. Since the process variables need only be sampled periodically, using a multiplexer provides a costeffective alternative to dedicated ADCs for each channel.

    Amplifier. Amplifiers arc used to scale the incoming signal up or down to be compatible with the range of the analogtodigital converter.

    Analogtndigital converter. As its name indicates, the function of the ADC is to convert the incoming analog signal into its digital counterpart.

let us consider the operation of the ADC, which is the heart of the conversion process. Analogtodigital conversion occurs in three phases: (1) sampling, (2) quantization, and (3) encoding. Sampling consists of converting the continuous signal into a series of discrete analog signals at periodic intervals. as shown in Figure 5.2. In quantization, each discrete analog signal is assigned to one of a finite number of previously defined amplitude levels. The amplitude levels are discrete values of voltage ranging over the full scale of the ADC In the encoding phase, the discrete amplitude levels obtained during quantization are converted into digital code, representing the amplitude level as a sequence of binary digits.

In selecting an analog-to-digital converter for a given application, the following factors are relevant: (I) sampling rate. (2) conversion time, (3) resolution, and (4) conversion method.

The sampling rate is the rate at which the continuous analog signals are sampled or polled. Higher sampling rates mean that the continuous waveform of the analog signal can be more closely approximated. When the incoming signals are multiplexed, the maximum possible sampling rate for each signal is the maximum sampling rate of the ADC divided by the number of channels that arc processed through the multiplexer. For example, if the maximum sampling rate of the ADC is HX)() sample/sec, and there are 10 input channels through the multiplexer, then the maximum sampling rate for each input line is 1000/10 = 100 sample/sec. (This ignores time losses due 10 multiplexer switching.)

The maximum possible sampling rate of an A DC is limited by the ADC conversion time. Conversion time of an ADC is the time interval between when an incoming signal is applied and when the digital value is determined by the quantization and encoding phases of the conversion procedure. Conversion time depends on (1) number of bits n used to define the converted digital value; as n is increased, conversion time increases (bad news), but resolution of the ADC improves (good news); and (2) type of conversion procedure used by the ADC

The resolution of an ADC is the precision with which the analog signal is evaluated. Since the signal is represented in binary form, precision is determined by the number of quantization levels, which in turn is determined by the bit capacity of the ADC and the computer. lhe number of quantization levels is defined as follows

where Nq ~ number of quantization levels: and n = number of bits. Resolution can be defined in equation form as follows:

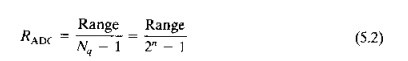
where R(ADC) =  resolution of the Anc. also called the quarui zationlevei spacing, which is the length of each quantization level; Range = fullscale range of the ADC, usually 010 V (the incoming signal must typically be amplified, either up or down, to this range); and N., = the number of quantization levels, defined in Eq. (5.1).

Quantization generates an error, because the quantized digital value is likely to be different from the true value of the analog signal. The maximum possible error occurs when the true value of the analog signal is on the horderline between two adjacent quantization levels;      in this case. the error         is onehalf the quantizationlevel spacing.  By this reasoning, the quantiration  error is defined:

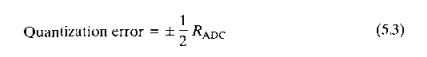
Various conversion methods arc available by which to encode an analog signal into its digital equivalent. Let us discuss one of the most common tcchniqucs,calted the succe.\sive approximation method. In this method, a series of known trial voltages are successively compared to the input signal whose value is unknown. The number of trial voltages corresponds to the number of bits used 10 encode the signal. The first trial voltage is onehalf the fullscale range of the ADC, and each successive trial voltage is onehalf the preceding value, Comparing the remainder of the input voltage with each trial voltage yields a bit value of"I" if the input exceeds the trial value and "0" if the input is less than the trial voltage. The successive hit values, multiplied by their corresponding trial voltage values, provide the encoded value of the input signal. Let us illustrate the procedure with an example.

DIGITAL-TO-ANALOG CONVERSION

where Eo = output voltage of the decoding step (V); Eler = reference voltage (V); and 81.82, ,B,; = status of successive bits in the register.O or 1.and n = the number of bits in the binary registcr ,

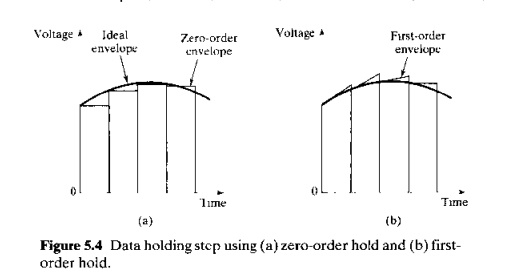
T'he obccuve in the data holding step ts 10 approximate the envelope termed by the data series, as illustrated in Figure 5.4. Data holding devices are classified according to the order of the extrapolation calculation used to determine the voltage output Juring sampling intervals. The most common extrapolator is a zeroorder hold, in which the output voltage between sampling instants is a sequence of step signals, as in Figure 5.4([1). The voltage function Juring the sampling interval is constant and can be expressed very simply as:

where E(r} = voltage as a function of time I during the sampling interval (V), and Eo = voltage output from the decoding step, Eq. (5.4).

The first-order data hold is less common than the zero-order hold, but it usually approximates the envelope of the sampled data values more closely. With the first-order hold, the voltage function £(t) during the sampling interval changes with a constant slope determined by the two preceding E" values. Expressing this mathematically, we have

where a = rate of change of E(t), Eo = output voltage from Eq.(5.4) at the start of the sampling interval (V), and t = time {secl.The value of a is computed each sampling interval as follows:

where Eo = output voltage from Eq. (5A) at the stan of the sampling interval (V), T = time interval between sampling instants (sec), and F.,,(T) = value of Evfrom Eq. (5.4) from the preceding sampling instant (removed backward in time by T, V). The result of the first-order hold is illustrated in Figure 5.4(bl.

A digital-to-analog converter uses a reference voltage of 100 V and has 6-bit precision. In three successive sampling instants, 0.5 sec apart, the data contained in the binary register are the following'

Determine: (a) the decoder output values for the three sampling instants and the voltage signals between instants 2 and 3 for (b) a zeroorder hold and (c) a first-order hold.

                                          The zero-order hold between sampling instants 2 and 3 yields a constant voltage E(t) = 65.63 V according to Eq. (5.5).

The first-order hold yields a steadily increasing voltage. The slope a is given by Eq. (5.7):

These values and functions are plotted in Figure 5.5. Note that the firstorder hold more accurately anticipates the value of EQ at sampling instant 3 than does the zero-order hold.