Design Problem, Important Question And Answer: Civil - Limit State Design Of Footing

 

2. Design an isolated footing for an R.C. column of size 230 mm x 230 mm which carries a vertical load of 500 kN. The safe bearing capacity of soil is 200 kN/m². Use M20 concrete and Fe 415 steel.

 

Solution

 

Step 1: Size of footing

 

Load on column = 600 kN

 

Extra load at 10% of load due to self weight of soil = 60 kN

 

Hence, total load, P = 660 kN

Required area of footing, - = _ _/01^. = _ ²²³₄₃₃ = 5. 5_6⁴

 

 

Assuming a square footing, the side of footing is 7 = 0 = _ )5. 5 = 8. 94_6

Hence, provide a footing of size 1.85 m x 1.85 m

Net upward pressure in soil, : =   ^;__   _ = 175.3_BC/E^, __ < 200_BC/E^, Hence O.K.

 

+.<=_>_+.<=

 

Hence, factored upward pressure of soil, p_u = 263 kN/m² and, factored load, P_u = 900 kN.

Step 2: Two way shear

 

Assume an uniform overall thickness of footing, D = 450 mm.

 

Assuming 12 mm diameter bars for main steel, effective thickness of footing 'd' is d = 450 - 50 - 12 - 6 = 382 mm

 

The critical section for the two way shear or punching shear occurs at a distance of d/2 from the face of the column (See Fig. 6), where a and b are the sides of the column.

Hence, punching area of footing = (a + d)² = (0.23 + 0.382)² = 0.375 m² here a = b =side of column

Punching shear force = Factored load - (Factored upward pressure x punching area of footing)

=  900 - (263 x 0.375)

=  801.38 kN

 

3.        Design an isolated footing for an R.C. column of size 300 mm x 300 mm which carries a vertical load of 800 kN together with an uniaxial moment of 40 kN-m. The safe bearing capacity of soil is 250 kN/m². Use M25 concrete and Fe 415 steel.

 

Solution

 

Step 1: Size of footing

 

Load on column = 800 kN

 

Extra load at 10% of load due to self weight of soil = 80 kN Hence, total load, P = 880 kN

 

Let us provide a square isolated footing, where L=B Equating the maximum pressure of the footing to SBC of soil,

^‰                        +_^Š_‹ = Œ•Ž_l

 

 

 

i.e.,  ⁹⁹³₀₄ +_^Z3₀^_V₅^_2 = 4\3

On solving the above equation, and taking the least and feasible value, B = 2 m

 

Hence, provide a square footing of size 2 m x 2 m

 

The maximum and minimum soil pressures are given by

T6PV = _ ⁹³³₄₄ +_^Z3₄^_V₅^_2 = 453 ^X[₆₄ < __250 ₆^X[₄ __•. •.

T6LI = _ ⁹³³₄₄ ?_^Z3₄^_V₅^_2 = 8e3 ₆^X[₄ _ y _''''____•. -.

Hence, factored upward pressures of soil are,

 

p_u,max  = 345 kN/m²  and  p_u,min  = 255 kN/m²

Further, average pressure at the center of the footing is given by

p_u,avg  = 300 kN/m²

and, factored load, P_u = 900 kN, factored uniaxial moment, M_u = 60 kN-m

 

Step 2: Two way shear

 

Assume an uniform overall thickness of footing, D = 450 mm

 

Assuming 16 mm diameter bars for main steel, effective thickness of footing 'd' is d = 450 - 50 - 16 - 8 = 376 mm

 

The critical section for the two way shear or punching shear occurs at a distance of d/2 from the face of the column (Fig. 9), where a and b are the dimensions of the column.

Hence, punching area of footing = (a + d)² = (0.30 + 0.376)² = 0.457 m² where a = b = side of column

Punching shear force = Factored load - (Factored average pressure x punching area of footing)

=  1200 - (300 x 0.457)

 

=  1062.9 kN

Therefore, nominal shear stress in punching or punching shear stress ?V is computed as     

Since the punching shear stress (1.05 N/mm²) is less than the allowable shear stress (1.25 N/mm²), the assumed thickness is sufficient to resist the punching shear force.

 

Hence, the assumed thickness of footing D = 450 mm is sufficient.

 

The effective depth for the lower layer of reinforcement, , d = 450 - 50 - 8 = 392 mm, and the effective depth for the upper layer of reinforcement, d = d = 450 - 50 - 16 - 8 = 376 mm.

 

 

Step 3: Design for flexure

 

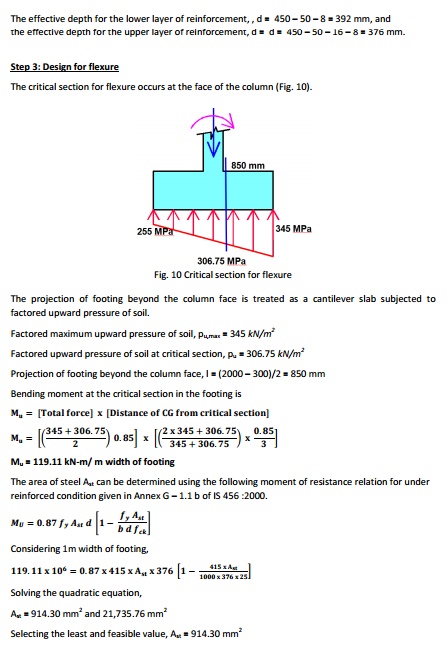
The critical section for flexure occurs at the face of the column (Fig. 10).

The projection of footing beyond the column face is treated as a cantilever slab subjected to factored upward pressure of soil.

 

Factored maximum upward pressure of soil, p_u,max = 345 kN/m²

 

Factored upward pressure of soil at critical section, p_u = 306.75 kN/m²

 

Projection of footing beyond the column face, l = (2000 - 300)/2 = 850 mm

 

Bending moment at the critical section in the footing is Š€

M_u = 119.11 kN-m/ m width of footing

 

Solving the quadratic equation,

 

A_st = 914.30 mm² and 21,735.76 mm²

 

Selecting the least and feasible value, A_st = 914.30 mm²

 

The corresponding value of p_t = 0.24 %

Hence from flexure criterion, p_t = 0.24 %

 

 

Step 4: One way shear

 

The critical section for one way shear occurs at a distance of 'd' from the face of the column (Fig. 11).

 

Step 5: Check for

 

Step 6: Check for bearing stress

The load is assumed to disperse from the base of column to the base of footing at rate of ₂₁₀₀H:1V. at he bottom of footing =