Chapter: Civil : Design Of Reinforced Concrete And Brick Masonry Structures- Design Of Staircase

Design Of Staircase

GEOMETRICAL TYPES OF STAIRCASE, STAIRCASE SPANNING TRANSVERSELY, STAIRCASE SPANNING LONGITUDINALLY, TREAD RISER STAIRCASE - (Civil - Design Of Reinforced Concrete And Brick Masonry Structures- Design Of Staircase)

DESIGN OF STAIRCASE

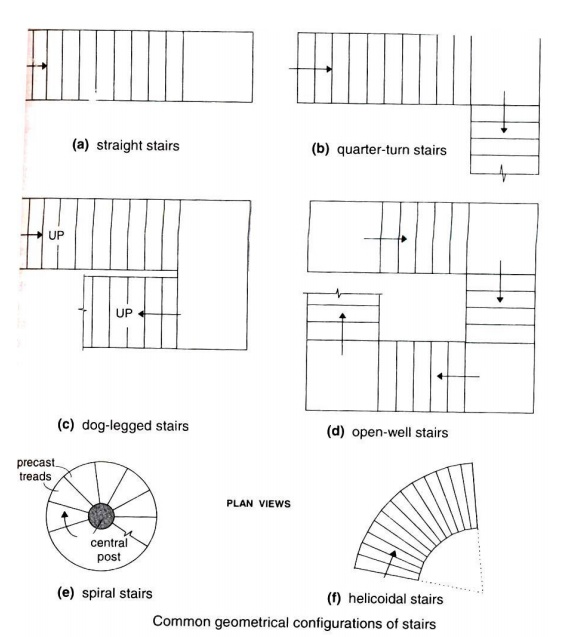
GEOMETRICAL TYPES OF STAIRCASE:

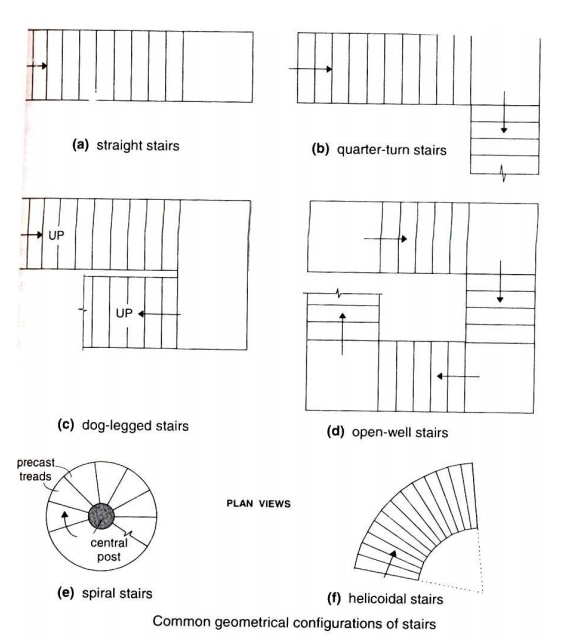
Based on loading and support conditions:

o Spanning along transverse direction

Cantilever staircase

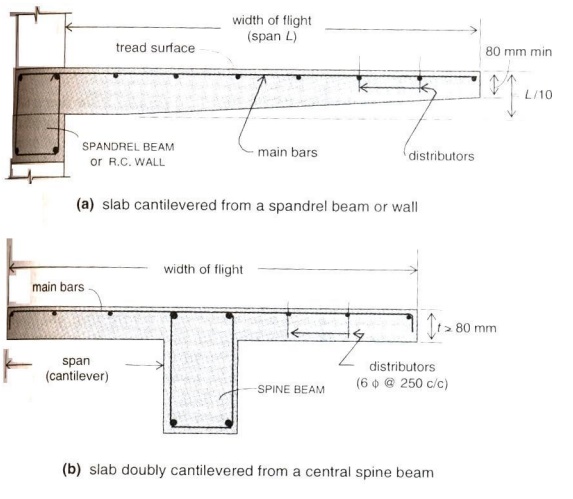
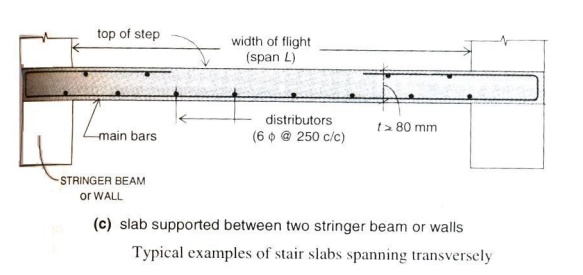
Slab supported between stringer beams

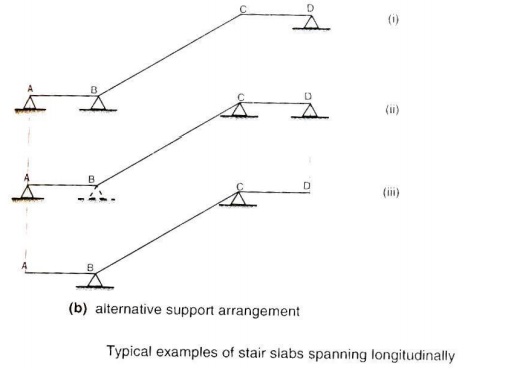
o Spanning along longitudinal direction

[Most commonly adopted]

Loading on staircase:

Dead load:

- Self weight of slab

- Self weight of step

- Tread finish [0.6 -1 kN/m²]

Live load:

For overcrowding ^� 5 kN/m²

No overcrowding ^� 3 kN/m²

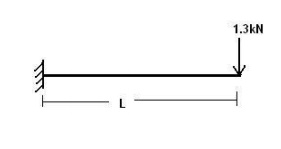
For independent cantilever state, the following live load condition is also checked:

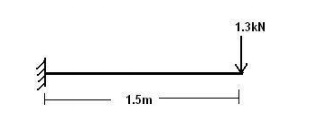
STAIRCASE SPANNING TRANSVERSELY

1) A straight staircase is made of structurally independent tread slab cantilevered from a RC wall. Given, the riser is 150mm and tread is 300mm with width of flight 1.5m. Design a typical cantilever tread slab. Apply live load for overcrowding. Use M20 concrete and Fe250 steel.

Loading on the staircase (0.3m width)

Dead load:

Self weight of tread slab = 25 x 0.15 x 0.3 = 1.125 kN/m

Floor finish (0.6 kN/m2) = 0.6 x 0.3 = 0.18 kN/m

Total = 1.305 kN/m

Dead load moment, M_D = 1.305 x 1.5² / 2 = 1.468 kNm

load: Maximum of,

i) Overcrowding ^� 5 kN/m² L.L. = 5 x 0.3 = 1.5 kN/m

M_L = wl²/2 = 1.5 x 1.5² / 2 = 1.69 kNm

ii)

M_L = 1.3 x 1.5 = 1.95 kNm

The maximum of the above two values is M_L = 1.95 kNm

Total moment = 1.468 + 1.95 = 3.42 kNm

Factored moment = 5.13 kNm

Effective depth = 150 -(20 + 10/2) = 125 mm

[Slab cover ^� 15mm to 20 mm]

3 nos. of 10mm ? are provided at the top.

Distribution steel:

MS ^� 0.15% of c/s ^� 0.15/100 x 300 x 150 = 67.5mm²

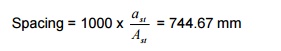
Provide 8mm @ 300 mm c/c Check for shear:

?_v = V_u / b.d

Shear force due to dead load = w.l = 1.305 x 1.5 = 1.958 kN Shear force due to live load,

i) 1.5 x 1.5 = 2.25 kN

ii) 1.3 kN

V_u = 2.25 + 1.958 = 4.208 kN

Factored Vu = 6.312 kN

As per Cl.40.2.1.1, IS456 -2000,_cvalue?is modified when thickness is less than 300mm Upto a depth of 150mm, ^� K = 1.3

When depth is > 300mm, ^� K = 1

Development length = ^f^.^s^s = 453.125 mm

Provide a development length of 450mm

Providing a 90⁰ bent, length required = 450 -80 = 370mm

?v= Vu / b.d = 0.168 N/mm²

For pt = 100 As / b.d

= 0.54%,

?_c = 1.3 x 0.4928 = 0.6406N/mm²

?_v< _c ?

Hence, safe.

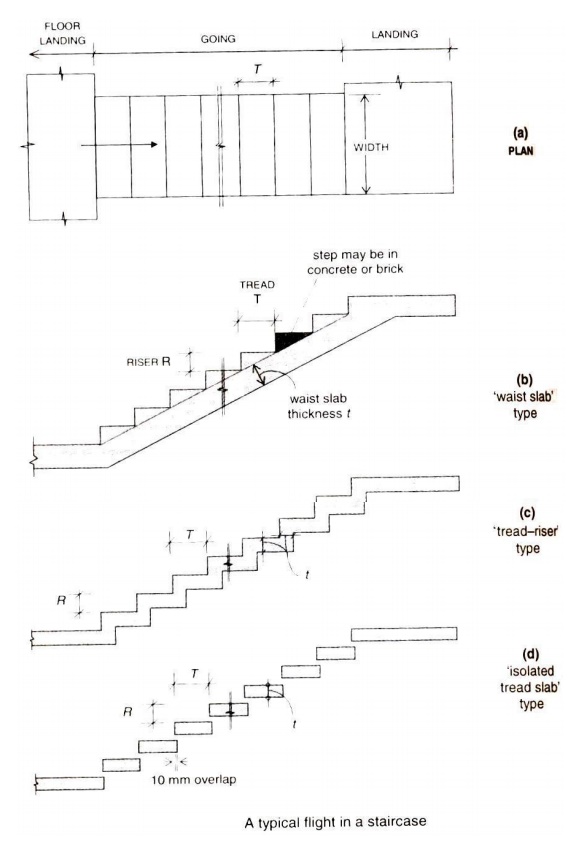
2) Design a waist slab type staircase comprising of a straight flight of steps supported between two stringer beams along the two sides. Assume an effective span 1.5m, a riser of 150mm and tread of 270mm. Assume a live load of 3kN/m². Use M20 concrete and Fe250 steel. Assume mild exposure condition.

The staircase is spanning along the transverse direction.

The main reinforcement should be provided along the transverse direction and distribution steel is provided at the top.

Inclined length of one step = Rt ( R ² +T ² ) = 308.87 mm ~ 309mm

The loading on the slab is found for an inclined width of 309mm, which is later converted for 1m length.

Assume l/d = 30 ^� 1500/d = 30 ^� d = 50mm Assume d = 60mm

D = 60 + cover + Bar dia./2 = 60 + 20 + 10/2 = 85mm

Loading on slab over each tread width:

Self weight of slab = 0.309 x 25 x 0.085 = 0.657 kN/m

Self weight of step = � x 0.15 x 0.27 x 25 = 0.50625 kN/m

Tread finish = 0.27 x 0.6 = 0.162 kN/m

Live load (3kN/m2) = 0.27 x 3 = 0.81 kN/m

Total = 2.135 kN/m

The load 2.135 kN/m acts vertically downwards. The load acting along the inclined slab is the cosine value of the above.

^� 2.135 x cos? = 2.135 (270/309) = 1.866 kN/m

The distributed load for 1m step along the inclined slab is 1.86 x 1/0.309 = 6.02 kN/m Factored load = 9.03 kN/m

M = wl²/8 = 9.03 x 1.5² / 8 = 2.54 kNm

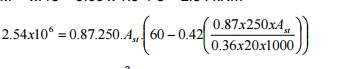
^� A_st = 205.72 mm²/m

Provide 8mm, spacing required is 240mm c/c Spacing < [300mm and 3d = 180mm] Provide 8mm @ 180mm c/c

Distribution steel: MS ^� 0.15% of c/s

= 0.15/100 x 1000 x 60 = 90mm²

Provide 6mm ?, spacing required = 314.15mm <

Provide 6mm @ 300mm c/c

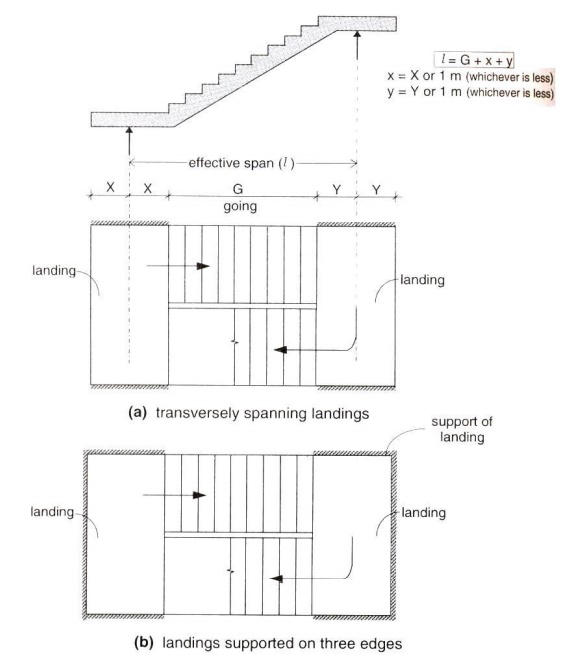
STAIRCASE SPANNING LONGITUDINALLY

1) Design the staircase slab shown in figure. The stairs are simply supported on beams provided at the first riser and at the edge of upper landing. Assume a floor finish of 0.8kN/m² and a live load of 5 kN/m². Use M20 concrete and Fe415 steel. Assume mild exposure condition.

L = 3 + 1.5 + (0.15 + 0.15) = 4.8m Assume L/d as 20,

4.8/d = 20 ^� d = 240mm

D = 240 + 20 + 10/2 = 265mm

Loading on going slab:

Length of the inclination of one step is Rt (R 2 + T 2) ,

Where, R = 150mm, T = 300mm

L = 335.41mm

Self weight of waist slab = 25 x (0.265 x (0.3354/0.3) = 7.4 kN/m²

Self weight of step = 25 x � x 0.15 = 1.875 kN/m²

Floor finish = 0.8 kN/m²

Live load = 5 kN/m²

Total = 15 kN/m²

Loading on going slab:

Self weight of slab = 25 x 0.265 = 6.625 kN/m²

Floor finish = 0.8 kN/m²

Live load = 5 kN/m²

Total = 12.425 kN/m²

Considering 1m strip,

The staircase slab is idealized as given below:

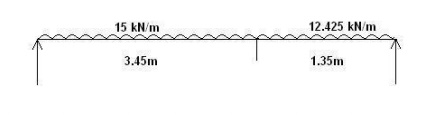
R_A x 4.8 -(15 x 3.45 x 3.075) -(12.425 x 0.675 x 1.35) = 0

R_A = 35.69 kN, R_B = 33.11 kN

Xo = R_A / udl = 35.69/15 = 2.37 m Moment at 2.37m is,

35.69 x 2.37 -(15 x 2.37 x 2.37/2) = 42.23 kNm Factored moment = 63.35 kNm

63.35 x 10⁶ = 86.625 x 10³.A_st -7.604.A_st²

A_st = 785.19 mm2

Provide 10mm @ 100mm c/c

Distribution steel:

0.12% of c/s ? 0.12/100 x 1000 x 265 = 318mm²

Provide 8mm @ 150mm c/c

Check for shear:

?v u=/b.d V

Maximum shear force = [35.69 -(15.08 x 0.24)] x 1.5 = 48.1 kN

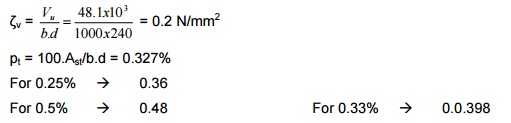
?_c= 0.398 N/mm²

The_cvalue? is modified based on Cl.40.2.1.1 for D = 265mm

For D = 150mm, 1.3

For D = 300mm, 1 For D = 265mm, 1.07

?_cmodified = 1.07 x 0.398 = 0.426 N/mm²

?_v< _c ?

Hence, safe.

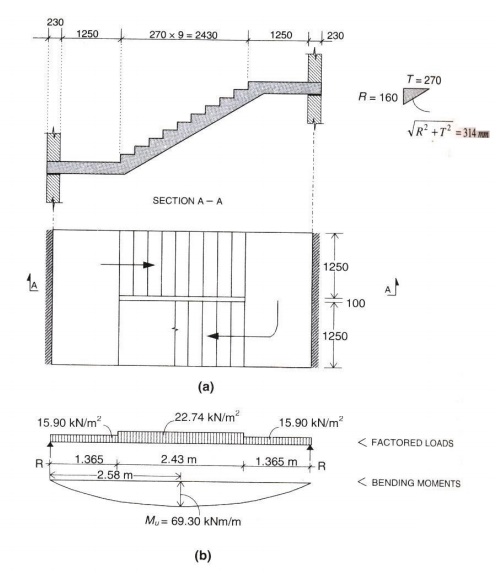
2) Design a dog legged staircase having a waist slab for an office building for the following data:

i) Height between floor = 3.2m

ii) Riser = 160mm

iii) Tread = 270mm

iv) Width of flight is equal to the landing width = 1.25m LL = 5 kN/m², FF = 0.6 N/mm²

Assume the stairs to be supported on 230mm thick masonry walls at the outer edges of the landing parallel to the risers. Use M20 concrete and Fe415 steel.

Note : Based on riser, number of steps is found. Based on tread, length of staircase is found. No. of steps = 3.2/0.16 = 20

10 numbers of steps are used for first flight and other 10 to the second flight.

Loading on going:

Self weight of waist slab = 25 x 0.283 x (0.31385/0.270) = 8.22 kN/m²

Self weight of step = 25 x � x 0.16 = 2 kN/m²

Tread finish = 0.6 kN/m²

Live load = 5 kN/m²

Total = 15.82 kN/m²

Loading on landing slab:

Self weight of slab = 25 x 0.283 = 7.075 kN/m²

l/d = 20 - > 5.16/d = 20

^� d = 258mm

D = 258 + 20 + 10/2 = 283mm

Length of inclination of one step,

R = 160mm, T = 270mm, L = 313.85mm

Self weight of slab = 25 x 0.283 = 7.075 kN/m²

FF = 0.6 kN/m²

LL= 5 kN/m²

Total = 12.675 kN/m²

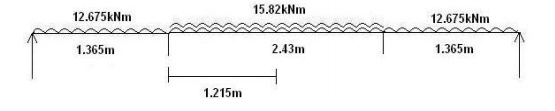
R_A x 5.16 -(12.675 x 1.365 x 4.4775) -(15.82 x 2.43 x 2.58) -(12.675 x 1.365 x 0.6875) = 0 R_A = 36.54 kN

R_B = 36.51 kN

Maximum moment at centre = 36.5 x 2.58 -(12.675 x 1.365 x (0.6825 x 1.215) -(15.82 x 1.215²/2) = 49.66 kNm

Factored moment = 74.49 kNm

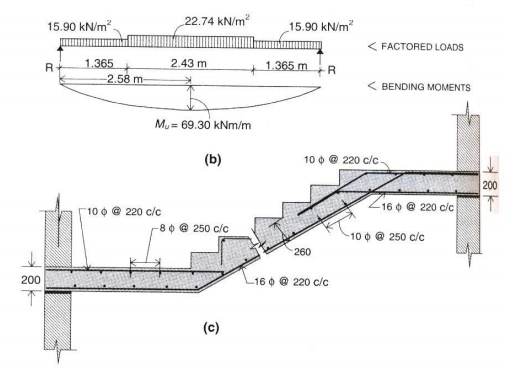
b = 1000mm, d = 258mm

74.49 x 10⁶ = 93.15 x 10³ A_st -7.4 A_st²

A_st = 868.99 mm²

Provide 12mm ? @ 130mm c/c

Distribution steel:

0.15% of c/s = 0.15/100 x 1000 x 283 = 424.5 mm² 8mm @ 110mm c/c

Check for shear: ?_v= V_u/b.d

Maximum shear force = [36.5 -(12.675 x 0.258)] x 1.5 = 49.84 kN ?_v= 0.193 N/mm²

?_c:

Pt = 100.Ast/b.d = 0.336%

For pt = 0.25% -> 0.36

For pt = 0.5% -> 0.48

For pt = 0.336% -> 0.40

?c = 0.40 N/mm2

Modification factor,

For D = 150mm, -> 1.3

For D = 300mm, -> 1

For D = 283mm, -> 1.03

?_cmodified = 1.03 x 0.40 = 0.412 N/mm²

?_v< _c ?

Safe in shear.

TREAD RISER STAIRCASE

Actual analysis ^� Theory of plates l/d limited to 25

Support conditions:

i) Transverse direction -Stair is spanning along transverse direction

ii) Longitudinal direction

iii) Stair slab spanning longitudinally and landing slab supported transversely

In Tread -Riser stair span by depth ratio is taken as 25 and the loading on the folded slab comprising the tread and riser is idealized as a simply supported slab with loading on landing slab and going similar to a waist like slab. The loading on folded slab includes,

i) self weight of tread riser slab

ii) floor finish

iii) live load ^� 5 kN/m² (overcrowded), 3 kN/m² (No overcrowding)

Note:

For staircase spanning longitudinally where the landing is supported along the transverse direction only. While finding the effective length along the longitudinal direction only half the length of the landing slab is considered. There is no change in the loading of going slab. But the loading on landing slab is half (waist type and tread-riser type). The landing slab is designed separately for the full load on landing plus half the loading from going slab.

1) Design a dog legged staircase having a tread-riser slab for an office building for the following data:

i) Height between floor = 3.2m

ii) Riser = 160mm

iii) Tread = 270mm

iv) Width of flight is equal to the landing width = 1.25m LL = 5 kN/m², FF = 0.6 N/mm²

Assume the stairs to be supported on 230mm thick masonry walls supported only on two edges perpendicular to the risers. Use M20 concrete and Fe415 steel.

The length of the landing slab is halved while finding the effective length along the longitudinal direction since the staircase is supported only on the landing slab along the transverse direction.

Effective length = 2.43 + 1.25 = 3.68m Assume l/d = 25, 3.68/d = 25

^� d = 147.2 mm ~ 150mm

D = 150 + (20 + 10/2) = 175mm

Loading on the going and landing slab: [Folder Tread Riser]

Self weight of tread riser = 25 x (0.27 + 0.16) x 0.175/0.27 x 1 = 6.97 kN/m2

Floor finish = 0.6 kN/m2

Live load = 5 kN/m2

Total = 12.57 kN/m2

Considering 1m strip, w = 12.57 kN/m

Loading on landing slab:

Self weight of slab = 25 x 0.175 = 4.375 kN/m²

Floor finish = 0.6 kN/m²

Live load = 5 kN/m²

Total = 9.975 kN/m²

Considering 1m strip, w = 9.975 kN/m

50% of load on landing slab is considered along the longitudinal direction. Along the longitudinal direction, the loading is,

R_A x 3.68 -(4.99 x 3.3675) -(12.57 x 1.84 x 2.43) -(4.99 x 0.3125 x 0.625) = 0

^�R_A = 18.39 kN

^�R_B = 18.39 kN

Moment at centre, (i.e. 1.84m),

M_max = 18.39 x 1.84 -(4.99 x 0.625 x 1.5275) -(12.57 x 1.215 x 0.675) = 19.79 kNm

Factored moment = 29.69 kNm For b = 1000mm, d = 150mm,

K = M_u/b.d²

^�A_st = 598.36 mm² / m

Provide 12mm ?, spacing required = 189mm

Provide 12mm @ 180mm c/c [Main bar as cross links on riser and tread]

Distribution steel:

0.12% of c/s = 0.12/100 x 1000 x 175 = 210 mm²

Provide 8mm @ 230mm c/c [Dist. bar along the width of stair]

Check for shear:

?v = Vu/b.d, Vu = [18.39 -(4.99 x 0.15)] x 1.5 = 26.46 kN

?v = 0.1764 N/mm2

?c :

100Ast/b.d. = 0.3989%

For pt = 0.25 -> 0.36

For pt = 0.5 -> 0.48

For pt = 0.39 -> (0.1584 + 0.2688) = 0.427

Modification factor (K):

For D = 150mm -> 1.3

For D = 300mm -> 1

For D = 175mm -> 1.08 + 0.17 = 1.25

?_cmodified = 0.534 N/mm²

?_v < _c. ? Hence safe in shear. Design of landing slab:

The landing slab is designed as a simply supported slab which includes the load directly acting on the landing and 50% of the load acting on the going slab.

The loading on the landing is,

i) Directly on landing = 9.98 kN/m

ii) 50% of load on going slab = (12.57 x 2.43)/2 = 15.27 kN/m

w = 25.25 kN/m l = 2.6m

Mu = wl²/8 x 1.5 = 32 kNm

b = 1000mm, d = 150mm K = Mu/b.d²

Ast = 650.19 mm2

Providing 12mm at bar, spacing required = 173.

Provide 12mm @ 170mm c/c Distribution steel:

0.12% of c/s

Provide 8mm @ 230mm c/c

3 numbers of 8mm bars are provided between the cross links as distribution bars. A nominal reinforcement of 10mm @ 200mm c/c is provided at the top of landing slab.

Note : Shear in tread riser slab is negligible. Check for shear is not required.

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

Civil : Design Of Reinforced Concrete And Brick Masonry Structures- Design Of Staircase : Design Of Staircase |