Design Of Brick Masonry: Solved Design Problems

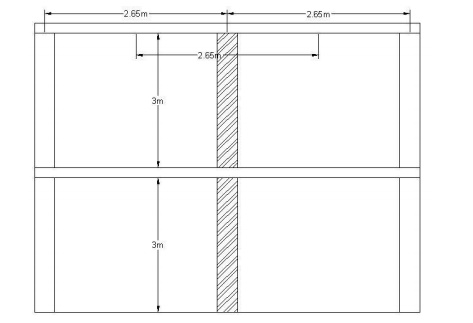
1. Design an interior cross wall for a two storeyed building to carry 100mm thick RC slab with 3m storey height. The wall is unstiffened and supports 2.65m wide slab. Loading on the slab is given as below:

i) Live load on floor slab = 2 kN/m²

ii) Live load on roof slab = 1.5 kN/m²

iii) Floor finish = 0.2 kN/m²

iv) Roof finish = 1.96 kN/m²

Assume the compressive strength of brick as 10N/mm² and mortar type as M1.

The loading on the wall includes the load from slab (LL + DL) and self weight of the wall. Assuming the wall thickness as 100mm and size of each masonry unit as 200 x 100 x 90mm,

Loading on slab: Live load:

on floor slab = 2 kN/m² on roof slab = 1.5 kN/m²

Dead load:

Floor finish = 0.2 kN/m² Roof finish = 1.96 kN/m²

Self weight of slabs = 2 x 0.1 x 25 = 5 kN/m² Load from slab = 10.66 kN/m²

For 2.65m length of slab,

Load from slab            = 10.66 x 2.658 = 28.36 kN/m

Self weight of masonry         = 2 x 0.1 x 20 x 3 = 12 kN/m

Total                              = 40.36 kN/m

Permissible stress of masonry for M1 mortar and masonry unit of compressive strength

10N/mm² is taken from Table 8, IS 1905 -1987.

Permissible stress = 0.96 N/mm²

Stress reduction factor, Area reduction factor, Shape modification factor are applied as per Cl.5.4.

Stress reduction factor (K_st)

Slenderness ratio (Least of l_e/t & h_e/t)

From Table 4,

h_e = 0.75 H = 0.75 x 3 = 2.25m     [Both ends fixed]

h_e/t = 2.25 / 0.1 = 22.5 < 27

Therefore, the stress reduction factor from T condition is,

For 22 -> 0.56     (e = 0)

For 24 -> 0.51                                

For 22.5 -> 0.55                             

Kst    = 0.55                                              

Area reduction factor (KA)  

                     [Cl.5.4.1.2, IS1905-1987]

A = 0.1 x 1 = 0.1m² < 0.2 m²

KA = 0.7 + (1.5 x 0.1) = 0.85

Shape modification factor (K_sh)     [Cl. 5.4.1.3, IS1905-1987]

Ksh for block of size 200 x 100 x 90 mm laid along 100mm side, from Table 10 for Height to Width ratio of 90 x 100,

^{Height/ Width = 90/100 = 0.9}

For 0.75x_o ^à 1

For 1x_o ^à 1.1

For 0.9x_o ^à 1.06

K_sh = 1.06

?_{per modified}   = Kst.KA.K_sh. ?_per

= 0.55 x 0.85 x 1.06 x 0.96 = 0.48 N/mm²

?act /m = 40.36x10³  / 100x1000  = 0.4036 N/mm² < ? _per [0.48 N/mm²]

Hence the adopted thickness of 100mm with M1 mortar and masonry unit with compressive strength 10N/mm² is safe in carrying the load from slab.

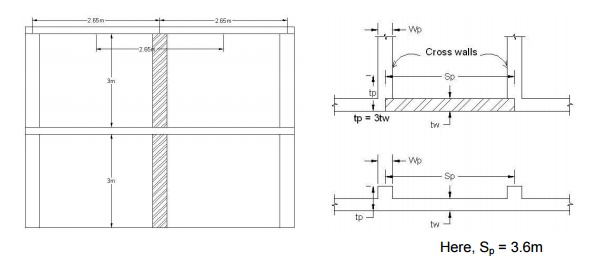
1.   2.In the above problem, design the wall if it is continuous and stiffened by cross wall of 100mm thickness and length of the wall being 3.6m.

Loading on the masonry wall = 40.36 kN/m

Actual stress = 40.36x1000  / 100x1000 = 0.4036 N/mm²

?_per for M1 mortar and masonry unit of compressive strength 10 N/mm² with 100mm thickness,

Permissible stress = 0.96 N/mm²  [From Table 8, IS1905 -1987]

Slenderness^àLeastratio,ofH_e/t&L_e/t ?

H_e = 0.75 H = 0.75 x 3 = 2.25m

L_e = 0.8L = 0.8 x 3.7 = 2.96m        [From Table 5, IS1905 -1987]

For the cross walls provided, stiffening coefficients are found from Table 6, IS1905 -1987. t_p ^à Thickness of pier

S_e = 1

Thickness of wall = 1 x 0.1 = 0.1m [Considering stiffness]

?        =   2.25   /   0.1   =   22.5   <   27

The stress reduction factor (K_st) for Table no.10 for ? = 22. condition,

For    ?   =   220.56

For ? = 240.51 For ? = 220.55.5

Kst = 0.55

Area reduction factor for area = 0.1 x 1 = 0.1m2 < 0.2m²,

KA = 0.7 + (1.5 x 0.1) = 0.85

Shape modification factor:   [Cl.5.4.1.3]

Ksh for block size of 200 x 100 x 90mm laid along 100mm side from Table 10 for height to width ratio of 90 x 100mm

Height/ Width = 90/100 = 0.9

For H_t/W = 0.75   1

For H_t/W = 1   1.1

For H_t/W = 0.9   1.06

K_sh = 1.06

?_{per modified}   = Kst.KA.Ksh. ?_per

= 0.55 x 0.85 x 1.06 x 0.96 = 0.48 N/mm² > _act?

Provided masonry wall of thickness 100mm with M1 mortar and compressive strength of each unit 10 N/mm² is safe.

3. Design an interior cross wall for a two storeyed building to carry 100mm thick RC slab. Check the safety of the wall if the wall is continuous and cross wall is available on only one side and the storey height is 3.5m. The wall supports 2.65m wide slabs on both sides. Loading on the slab is given as below:

i) Live load on floor slab = 2 kN/m²

ii) Live load on roof slab = 1.5 kN/m²

iii) Floor finish = 0.2 kN/m²

Roof finish = 1.96 kN/m²

Assume the compressive strength of brick as 10N/mm² and mortar type as M1. Loading on slab:

Live load:

on floor slab = 2 kN/m² on roof slab = 1.5 kN/m²

Dead load:

Floor finish = 0.2 kN/m² Roof finish = 1.96 kN/m²

Self weight of slabs = 2 x 0.1 x 25 = 5 kN/m² Load from slab = 10.66 kN/m²

For 2.65m length of slab, Load from slab

Self weight of masonry Total

?_{act /m} = 42.36x103 /100x1000 = 0.4236 N/mm²

Permissible stress of masonry for M1 mortar and masonry unit of compressive strength 10N/mm² is taken from Table 8, IS 1905 -1987.

Permissible stress = 0.96 N/mm²

Stress reduction factor, Area reduction factor, Shape modification factor are applied as per Cl.5.4.

Stress reduction factor (K_st)

Slenderness ratio (Least of le/t & he/t)  

From Table 4,             

Effective height, he = 0.75 H = 0.75 x 3.5 = 2.625m         [Both ends fixed]

Effective length, le = 1.5 L = 1.5 x 3.65 = 5.475m   [One end fixed, other end free]

h_e/t = 2.625 / 0.1 = 26.25 < 27

Therefore,                  the   stress   reduction   factor   from

condition is,

For 26 ^à 0.45      (e = 0)

For 27 ^à 0.43

For 26.25 ^à 0.3375 + 0.1075 = 0.445

K_st = 0.445

Area reduction factor (K_A)   [Cl.5.4.1.2, IS1905-1987]

A = 0.1 x 1 = 0.1m² < 0.2 m²

K_A = = 0.7 + (1.5 x 0.1) = 0.85

Shape modification factor (K_sh)     [Cl. 5.4.1.3, IS1905-1987]

K_sh for block of size 200 x 100 x 90 mm laid along 100mm side, from Table 10 for Height to Width ratio of 90 x 100,

^{Height/ Width = 90/100 = 0.9}

For 0.75x_o ^à 1

For 1x_o ^à 1.1

For 0.9x_o ^à 1.06

K_sh = 1.06

?per modified   = Kst.KA.Ksh. ?per

= 0.445 x 0.85 x 1.06 x 0.96 = 0.385 N/mm² < _act?_/m [0.4236 N/mm²]

Hence the adopted thickness of 100mm with M1 mortar and masonry unit with compressive strength 10N/mm² is not safe in carrying the load from slab. The thickness of wall is increased to 200mm.

Load from slab = 10.66 kN/m2                                           

For 2.65m length of slab,                                           

Load from slab   = 10.66 x 2.658 = 28.36 kN/m²              

Self weight of masonry= 2 x 0.2 x 20 x 3.5 = 28 kN/m              

Total = 56.36 kN/m                                  

Loading on masonry wall = 56.36 kN/m                            

Actual  actstress= 56.36x1000 /   200x1000 ?=0.2818 N/mm2        

Permissible stress of masonry for M1 mortar and masonry unit of compressive strength         

10N/mm² is taken from Table 8, IS 1905 -1987.                       

Permissible  ? _per= 0.96stressN/mm²                                 

Stress reduction factor, Area reduction factor, Shape modification factor are applied as per   

Cl.5.4.                                

Stress reduction factor (Kst)                                               

Slenderness ratio (Least of le/t & he/t)                              

From Table 4,                                                    

Effective height, he = 0.75 H = 0.75 x 3.5 = 2.625m         [Both ends fixed]        

Effective length, le = 1.5 L = 1.5 x 3.65 = 5.475m   [One end fixed, other end free]    

                   h_e/t = 2.625 / 0.2 = 13.125 < 27    

                   Therefore,   the   stress   reduction       

                   22.5 and no eccentricity condition is,    

                   For 12 - >  0.84   (e = 0)                 

                   For 14 - >  0.78                     

For 13.125 ^à 0.3675 + 0.439 = 0.806

K_st = 0.806

Area reduction factor (K_A)    [Cl.5.4.1.2, IS1905-1987]

A = 0.2 x 1 = 0.2m²

K_A = 1

Shape modification factor (K_sh)     [Cl. 5.4.1.3, IS1905-1987]

K_sh for block of size 200 x 100 x 90 mm laid along 100mm side, from Table 10 for Height to Width ratio of 90 x 100,

Height/ Width = 90/100 = 0.9

For 0.75x_o ^à 1

For 1x_o ^à 1.1

For 0.9x_o ^à 1.06

K_sh = 1.06

?per modified   = Kst.KA.Ksh. ?per

= 0.806 x 1 x 1.06 x 0.96 = 0.82 N/mm² > _act?_/m [0.2818 N/mm²]

Hence the adopted thickness of 200mm with M1 mortar and masonry unit with compressive strength 10N/mm² is safe in carrying the load from slab.

4. Design the interior wall of a single storey building shown in figure. The height of the ceiling is 3.5m and the load from slab including self weight is 30kN/m².

Load from slab = 30 x 3.65           = 109.5 kN/m

Self weight of wall = 0.15 x 3.5 x 1 x 20  = 10.5 kN/m

Total                                                 = 120 kN/m

Actual stress = 120x1000 / 150x1000 = 0.8 N/mm²

Permissible stress of masonry for M1 mortar and masonry unit of compressive strength 10N/mm² is taken from Table 8, IS 1905 -1987.

2

Permissible_per= 0.96stressN/mm   ?

Stress reduction factor, Area reduction factor, Shape modification factor are applied as per Cl.5.4.

Stress reduction factor (K_st)

Slenderness ratio (Least of l_e/t & h_e/t)

From Table 4,

Effective height, h_e = 0.75 H = 0.75 x 3.5 = 2.625m          [Both ends fixed]

Effective length, le = 1 L = 1.0 x 8.15 = 8.15m

h_e/t = 2.625 / 0.2 = 13.125 < 27

For the cross walls provided, stiffening coefficients are found from Table 6, IS1905 -1987.

S_e = 1

Thickness of wall = 1 x 0.2 = 0.2m [Considering stiffness]

?        =   2.625   /   0.2   =   17.5   <   27

Therefore, the stress reduction factor from Table 10 for ? = 17.5 condition is,

For 16 ^à 0.73      (e = 0)

For 18 ^à 0.67

For 13.125 ^à 0.1825 + 0.5025 = 0.685

K_st = 0.685

Area reduction factor (K_A)              [Cl.5.4.1.2, IS1905-1987]

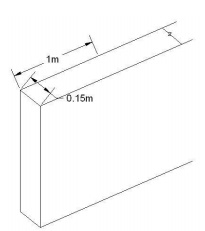
A = 0.15 x 1 = 0.15m²

K_A = 0.7 + (1.5 x 0.15) = 0.925

Shape modification factor (K_sh)     [Cl. 5.4.1.3, IS1905-1987]

K_sh for block of size 200 x 100 x 90 mm laid along 100mm side, from Table 10 for Height to Width ratio of 90 x 100,

Height/ Width = 90/100 = 0.9

For 0.75x_o ^à 1

For 1x_o ^à 1.1

For 0.9x_o ^à 1.06

K_sh = 1.06

?per modified      = Kst.KA.Ksh. ?per

= 0.685 x 0.925 x 1.06 x 0.96 = 0.647 N/mm² < _act?_/m [0.8 N/mm²]

Hence the adopted M1 mortar and masonry unit with compressive strength 10N/mm² is not sufficient in carrying the load.

Increase the strength of brick unit and mortar as,

H1 mortar and masonry unit compressive strength 15N/mm²

?_per             = 1.31 N/mm²

?_{per modified}      = 0.88 N/mm²

Therefore, the interior wall of 150mm thickness is safe with H1 mortar and brick units of compressive strength 15 N/mm².

5. Design a masonry wall of height 4m subjected to a load of 20kN/m. Use M1 mortar. The wall is unstiffened[no need to find effective length] at the ends.

Assume a thickness of wall of 300mm

Actual stress =  20x1000 / 300x1000 = 0.066N/mm²

?_per             = 0.96 N/mm²

H_e = 0.75 H = 0.75 x 4 = 3m

?  = 3/0.3 = 10

K_st = 0.89

For A = 0.3 x 1 = 0.3 m2, KA = 1 K_sh = 1.06

?_{per modified} = 0.27 N/mm² > _act?[0.066 N/mm²] Hence, safe.

6. Design the wall in the GF level for the loading condition as shown in figure.

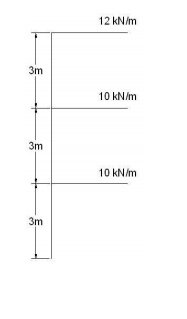
Loading on brick wall:

Load from slab = 12 + 10 + 10 Weight of wall = 32 kN/m

(self wt.) = 3 x 2 x 0.1 x 3 x 20  = 36 kN/m

Total  = 68 kN/m

Actual stress = 68x1000 / 2x100x1000 = = 0.34 N/mm²

Use M1 mortar and brick of compressive strength 10 N/mm². ?_per = 0.96 N/mm² [From Table 8, IS1905 -1987]

(?      ?   6)

h_eff = 0.75 x h = 0.75 x 3 = 2.25m

t_e = 2/3(t_w + t_w) = 2/3(0.1 + 0.1) = 0.133m

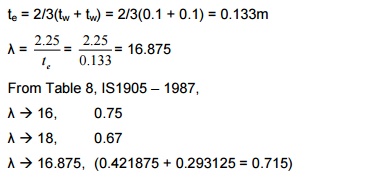
?^à 16.875,  (0.421875 + 0.293125 = 0.715)

Area of wall (each leaf) = 0.1 x 1 = 0.1m² < 0.2 m² K_A = 0.85

K_sh = 1.06

?per (modified)     = Kst x KA x Ksh x per?

= 0.704 x 0.85 x 1.06 x 1.96 = 0.61 N/mm² > _act?

Therefore, the cavity wall is safe with M1 mortar and masonry unit of compressive strength 10N/mm².

2.Design a cavity wall of overall thickness 250mm and thickness of each leaf 100mm for a three storeyed building. The wall is stiffened by intersecting walls 200mm thick at 3600mm c/c. The ceiling height is 3m and the loading from roof is 16 kN/m. The loading from each floor is 12.5kN/m.

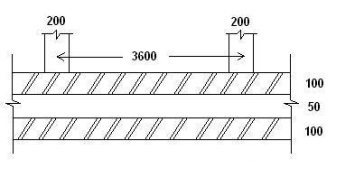
Load from roof      = 16kN/m

Load from floor     = 12.5 + 12.5 kN/m

Wall load [3x0.2x20]      = 36 kN/m

Total  = 77 kN/m

Actual   stress = ?_ac=  77x10³ / 200x1000 = ==0 .39N/mm²

?per :

Assume M1 mortar and brick of compressive strength 10 N/mm². From Table 7, IS1905 -1987,

?_per = 0.96 N/mm² (? ? 6) Effective height = h_eff = 0.75 x 3 = 2.25m

Effective length = l_eff = 0.8 l = 0.8 x 3600 = 2880mm = 2.88m Stiffening Coefficient:

Since cross wall is available along one leaf, Sc for

3. Design a masonry column to carry a load of 150kN. The height of the column is 2000mm. The column is restrained against translation (hinged) only.

Assume a column of size 400 x 400mm.

Use M1 mortar and brick of compressive strength 10 N/mm².

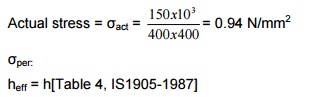
h_eff = h [Table 4, IS1905-1987]

?        =   2000/400   =   5   <   6

There is no need for Stress reduction factor (K_st = 1)

2

From       Table_per=0.967,N/mm?

A_st = 0.4 x 0.4 = 0.16m² < 0.2m² K_A = 0.7 + (1.5 x 0.4 x 0.4) = 0.94 K_sh = 1.06

?_{per (modified)} = 0.94 x 0.96 x 1 x 1.06 = 0.98 N/mm².

?act < per?

Therefore, the masonry column of size 400 x 400mm with M1 mortar and brick unit of compressive strength 10N/mm² is safe to carry a load of 150kN.

Note: Boundary condition is assumed if not given.

4.Design an interior wall of a single storeyed workshop building of height 5.4m supporting a RC roof. Assume roof load as 45kN/m. The wall is stiffened by piers at equal intervals shown in figure. Height = 5.4m, w = 45 kN/m

Since there is an increase in width at the pier, the actual stress is found for the wall length of 3.6m (One bay).

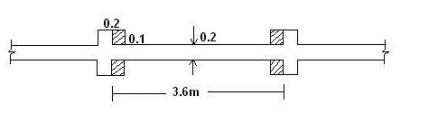
C/s area of one bay = (3.6 x 0.2) + 4(0.1 x 0.1) = 0.76 m²

?per:

h_eff = 0.75h = 4.05m [Table 4, IS1905-1987] demise leff = 0.8l = 0.8 x 3.6 = 2.88m

?        =   2.88   <   6

There is no need for Stress reduction factor (K_st = 1)

2

From       Table_per=0.967,N/mm?

A_st = 0.4 x 0.4 = 0.16m² < 0.2m² K_A = 0.7 + (1.5 x 0.4 x 0.4) = 0.94 K_sh = 1.06

?_{per (modified)} = 0.94 x 0.96 x 1 x 1.06 = 0.98 N/mm².

?act < per?

Therefore, the masonry column of size 400 x 400mm with M1 mortar and brick unit of compressive strength 10N/mm² is safe to carry a load of 150kN.

Stiffening coefficient,

?per (modified) = 0.785 x 0.96 x 1 x 1.06 = 0.79 N/mm² > _act?

Inference : Hence the brick wall is safe with M1 mortar and brick of compressive strength 10N/mm².

5.Design a brick masonry column of height 3m, tied effectively, fixed at top and bottom. The load from slab is 100kN, including self weight of the brick pillar.

Load from slab = 100Kn

Self weight of brick pillar = 0.4 x 0.4 x 20 x 3 = 9.6kN

Total = 109.6 kN

Assume a column size of 400mm x 400mm.

Actual stress = 109.6x103  / 400x400 = 0.685 N/mm²

Assume grade of mortar as M1 and compressive strength of 0.96N/mm² h_eff = 0.75.H = 2.25m

There is no need of stress reduction factor. K_st = 1

A = 0.4 x 0.4 = 0.16 m² < 0.2m² K_A = 0.7 + (1.5 x 0.4 x 0.4) = 0.94

K_sh = 1.06    [Brick unit 200 x 100 x 90]

?_{per (modified)} = 0.9565 N/mm² > _act?

Hence the brick wall is safe with M1 mortar and compressive strength of 10N/mm².

6.Design an interior wall of a 3 storeyed building with ceiling height of each storey as 3m. The wall is unstiffened and 3.6m in length. Load from roof is 12kN/m and from each floor is 10kN/m. Select a cavity wall with overall thickness 250mm and length between each leaf as 50mm.

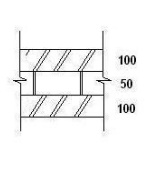
h = 3m, l = 3.6m

Load from roof                                = 12 kN/m

Load from each floor                               = 10 + 10 kN/m

Self weight of wall   = 3 x 2 x 0.1 x 3 x 20 = 36 kN/m

Total  = 68 kN/m

Use M1 mortar and brick of compressive strength 10N/mm², ?_per = 0.96 N/mm²

h_eff = 0.75 x 3 = 2.25m t_e = 2/3(t_w + t_w) = 0.133m

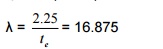
From Table 8, IS1905 -1987, K_st = 0.704

Area of wall = 0.1 x 1 = 0.1 m² < 0.2 m² K_A = 0.85

K_sh = 1.06

?_{per (modified)} = 0.704 x 0.85 x 1.06 x 0.96 = 0.61 N/mm² > _act?

Hence the brickwork is safe with M1 mortar and brick of compressive strength 10N/mm².