Chapter: Biochemistry: Enzyme Kinetics
Derivation of M - M Equation
Derivation of M - M Equation
Leonor Michaelis and Mand L. Menton in 1913
proposed a successful explanation for the effect of substrate concentration on
the enzyme activity.
According to them the enzyme E , and the
substrate S combines rapidly to form a complex, the enzyme substrate complex
ES. This complex then breaks down relatively and slowly to form the product P
of the reaction .These sequence of reactions can be represented in the
following equations

o K1& k2 are the rate
constants of the forward and backward reactions (step 1)
o K3& k4 are the rate
constants of the forward and backward reactions respectively (step2)
This is true only for the enzyme reactions which
fulfill the following conditions:
i.
only
a single substrate and a single product are involved.
ii.
the
reaction proceeds essentially to completion.
iii.
the
concentration of the substrate is much greater than that of the enzyme in the
system.
iv.
an
intermediate enzyme substrate complex is formed.
v.
the
rate of decomposition of the substrate is proportional to the concentration of
the enzyme substrate complex.
It is assumed that
the concentration of S is much greater than that of E and that only initial
velocities are measured,where only a small fraction of S has been converted.
Under these conditions, concentration of P ® ES can be ignored.
Applying law of mass action to the first step of
the reaction in which k1 and k2 are the rate constants
for the forward and backward reaction respectively,
The rate of forward reaction = k1 [E] [S]……………………………..(1)
The rate of backward reaction=k2 [ES]……………………………………..(2)
Applying law of mass action to the second step
of the reaction in which k3 and k4 are the rate constants
for the forward and backward reaction respectively,
The rate of forward reaction = k3 [ES]……………………….(3)
The rate of backward reaction can be neglected.
The total enzyme in the system can be
represented as,
[Et] =
[E] + [ES]……………………….(4)
Where [E] is the uncombined free enzyme
concentration, [ES] the enzyme substate concentration and [Et] the total enzyme
concentration. The velocity of the overall reaction is
V = k3 [ES] ………………………..(5)
This is the actual rate equation for the overall
reaction but it is not useful since neither k3 nor [ES] can be
measured directly. It is assumed that the reaction proceeds at steady state
where the rate of formation of [ES] equals to the rate of degradation of [ES].
The rate of formation of ES, Vf is
proportional to E and S as in any second order reaction.
Vf
= k1 [E] [S]
= k1 ([Et] – [ES]) [S]
………………………..(6)
The rate of disappearance of (ES), Vd
is
Vd=
k2 [ES] + k3 [ES]
=k2+k3 [ES]
…………….(7)
Since in the steady state Vd=Vf
k1( [Et] – [ES] ) [S] =k2 +
k3 [ES] …………………….(8)
Rearranging this equation gives
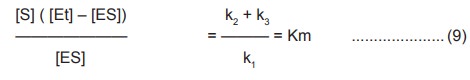
where Km is the Michaelis – Menton constant, an
useful parameter characteristic of each enzyme and a substrate.
Rearranging this equation by solving for [ES]

According to the previous equation (5), V =k3
[ES] . Substituting the value of [ES] (11) in this equation we get ,
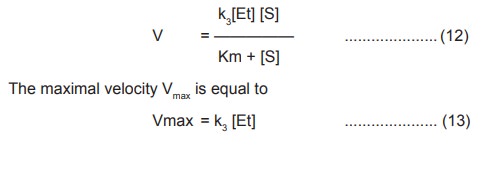
substituting the value of k3 [Et] in
the equation (12), the final Michaelis – Menton rate equation becomes,

Rearranging,
Km + [S] = 2 [S]
Therefore,
Km
=[S]
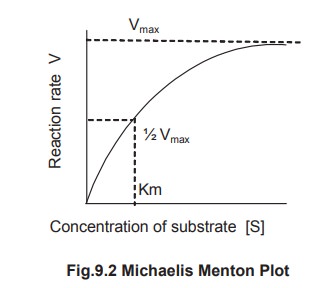
1. Km Value Definition
Km is defined as the concentration of the
substrate at which the velocity of the reaction is half maximal. It is
independent of enzyme concentration. The unit of Km is moles per litre. Thus,
Michaelis – Menton constant may be determined by a plot commonly known as M-M
plot obtained by plotting substrate concentration [S] versus rate of the
reaction [V] (Fig 9.2).
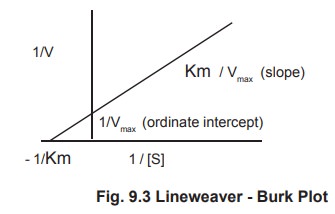
2. Lineweaver – Burk Equation
Transformation of the Michaelis – Menton equation.
The value of Km may be obtained more accurately
from the Lineweaver - Burk equation which is obtained by taking the reciprocal
of both sides of the Michaelis – Menton equation.
1/V = Km + [S] / Vmax [S] (1)
Rearranging this equation ,we have
1/V = Km / Vmax [S] + [S] / Vmax
[S] (2)
which is further simplified to
1/V = Km / Vmax . 1/ [S] + 1/ Vmax (3)
A plot of 1/V versus 1/S (a double reciprocal plot) yields a straight line with the slope of Km /Vmax and ordinate intercept of 1/ Vmax. Since the slope and intercept are readily measured from the graph, the Vmax and Km can be accurately determined (Fig 9.3).