Chapter: Physics : Higher Secondary School
Electric Field: Definition of Electric lines of force and Properties of lines of forces
Electric Field
Electric field due to a charge is the space around the test charge in which it experiences a force. The presence of an electric field around a charge cannot be detected unless another charge is brought towards it.
When a test charge qo is placed near a charge q, which is the source of electric field, an electrostatic force F will act on the test charge.
Electric Field Intensity (E)
Electric field at a point is measured in terms of electric field intensity. Electric field intensity at a point, in an electric field is defined as the force experienced by a unit positive charge kept at that point.
It is a vector quantity.
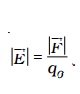
The unit of electric field intensity is N C-1.
The electric field intensity is also referred as electric field strength or simply electric field. So, the force exerted by an electric field on a charge is F = qoE.
1. Electric field due to a point charge
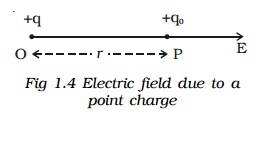
Let q be the point charge placed at O in air (Fig.1.4). A test charge qo is placed at P at a distance r from q. According to Coulomb's law, the force acting on qo due to q is
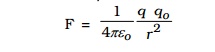
The electric field at a point P is, by definition, the force per unit test charge.
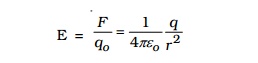
The direction of E is along the line joining O and P, pointing away from q, if q is positive and towards q, if q is negative.
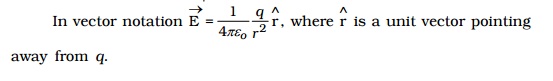
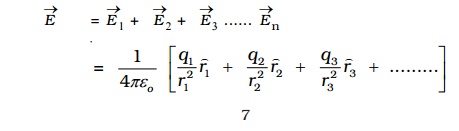
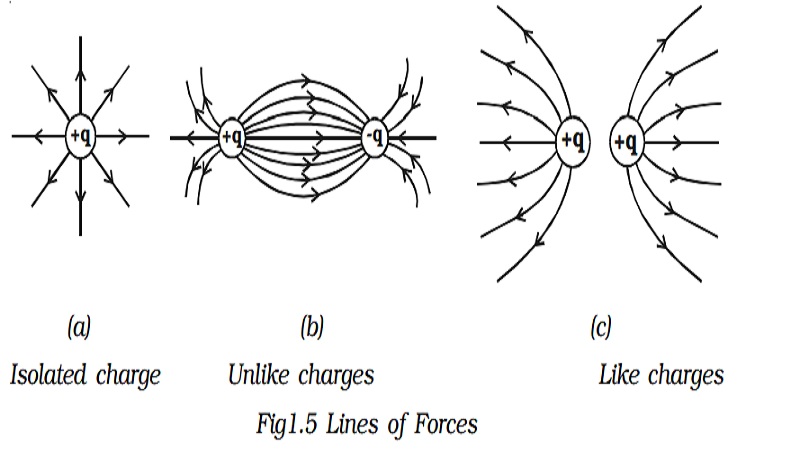
3. Definition of Electric lines of force
Definition of Electric lines of force and Properties of lines of forces:
The concept of field lines was introduced by Michael Faraday as an aid in visualizing electric and magnetic fields.
Electric line of force is an imaginary straight or curved path along which a unit positive charge tends to move in an electric field.
The electric field due to simple arrangements of point charges are shown in diagram.
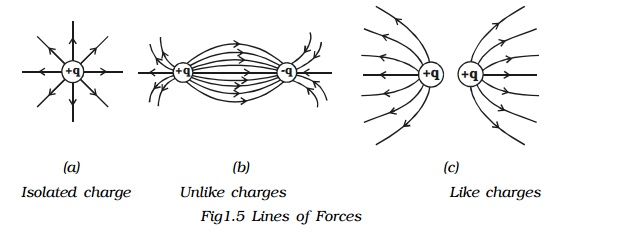
Properties of lines of forces:
x Lines of force start from positive charge and terminate at negative charge.
x Lines of force never intersect.
x The tangent to a line of force at any point gives the direction of the electric field (E) at that point.
x The number of lines per unit area, through a plane at right angles to the lines, is proportional to the magnitude of E. This means that, where the lines of force are close together, E is large and where they are far apart, E is small.
4. Electric dipole and electric dipole moment
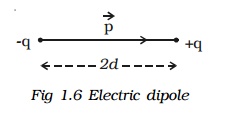
Two equal and opposite charges separated by a very small distance constitute an electric dipole.
Water, ammonia, carbon?dioxide and chloroform molecules are some examples of permanent electric dipoles. These molecules behave like electric dipole, because the centres of positive and negative charge do not coincide and are separated by a small distance.
Two point charges +q and -q are kept at a distance 2d apart (Fig.1.6). The magnitude of the dipole moment is given by the product of the magnitude of the one of the charges and the distance between them.
? Electric dipole moment, p = q2d or 2qd.
It is a vector quantity and acts from -q to +q. The unit of dipole moment is C m.
5. Electric field due to an electric dipole at a point on its axial line.
AB is an electric dipole of two point charges -q and +q separated by a small distance 2d (Fig 1.7). P is a point along the axial line of the dipole at a distance r from the midpoint O of the electric dipole.
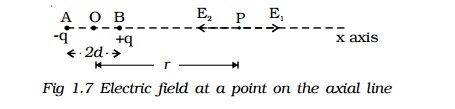
The electric field at the point P due to +q placed at B is,
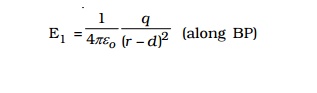
The electric field at the point P due to xq placed at A is,

Therefore, the magnitude of resultant electric field (E) acts in the direction of the vector with a greater magnitude. The resultant electric field at P is,

[? Electric dipole moment p = q x 2d]
E acts in the direction of dipole moment.
6. Electric field due to an electric dipole at a point on the equatorial line.
Consider an electric dipole AB. Let 2d be the dipole distance and p be the dipole moment. P is a point on the equatorial line at a distance r from the midpoint O of the dipole (Fig 1.8a).
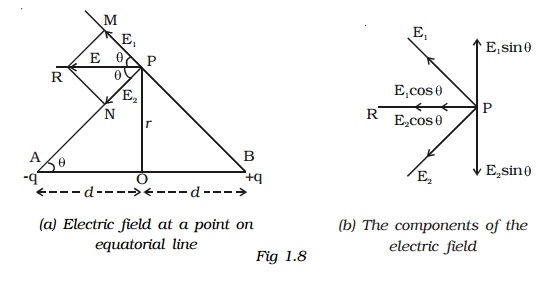
Electric field at a point P due to the charge +q of the dipole,

The magnitudes of E1 and E2 are equal. Resolving E1 and E2 into their horizontal and vertical components (Fig 1.8b), the vertical components E1 sin θ and E2 sin θ are equal and opposite, therefore they cancel each other.
The horizontal components E1 cos θ and E2 cos θ will get added along PR.
Resultant electric field at the point P due to the dipole is
E = E1 cos θ + E2 cos θ (along PR)
= 2 E1cos θ (?E1 = E2)
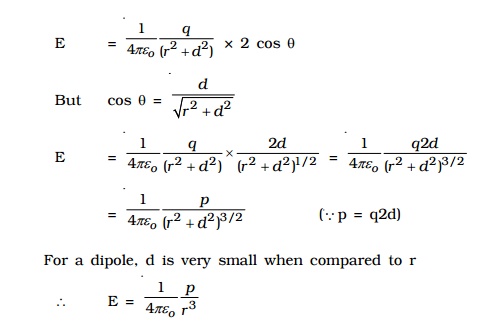
The direction of E is along PR, parallel to the axis of the dipole and directed opposite to the direction of dipole moment.
7. Electric dipole in a uniform electric field
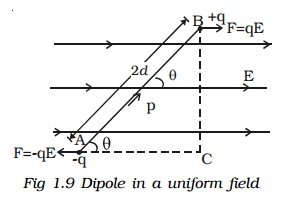
Consider a dipole AB of dipole moment p placed at an angle ? in an uniform electric field E (Fig.1.9). The charge +q experiences a force qE in the direction of the field. The charge -q experiences an equal force in the opposite direction. Thus the net force on the dipole is zero.
The two equal and unlike parallel forces are not passing through the same point, resulting in a torque on the dipole, which tends to set the dipole in the direction of
the electric field.
The magnitude of torque is,
τ = One of the forces x perpendicular distance between the forces
= F x 2d sin
= qE x 2d sin ? = pE sin θ
( q x 2d = P)

Note : If the dipole is placed in a non?uniform electric field at an angle θ,, in addition to a torque, it also experiences a force.
8. Electric potential energy of an electric dipole in an electric field.
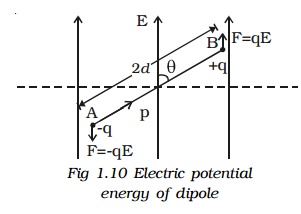
Electric potential energy of an electric dipole in an electrostatic field is the work done in rotating the dipole to the desired position in the field.
When an electric dipole of dipole moment p is at an angle ? with the electric field E, the torque on the dipole is
τ = pE sin θ
Work done in rotating the dipole through dθ,
dw = τ.dθ
= pE sinθ.dθ
The total work done in rotating the dipole through an angle θ is
W = ∫dw
W = pE ∫sinθ.dθ = �'pE cos θ
This work done is the potential energy (U) of the dipole.
∴ U = �' pE cos θ
When the dipole is aligned parallel to the field, θ = 0o
∴U = �'pE
This shows that the dipole has a minimum potential energy when it is aligned with the field. A dipole in the electric field experiences a torque (�'τ = �'p x�'E) which tends to align the dipole in the field direction, dissipating its potential energy in the form of heat to the surroundings.
Microwave oven
It is used to cook the food in a short time. When the oven is operated, the microwaves are generated, which in turn produce a non?uniform oscillating electric field. The water molecules in the food which are the electric dipoles are excited by an oscillating torque. Hence few bonds in the water molecules are broken, and heat energy is produced. This is used to cook food.
Related Topics