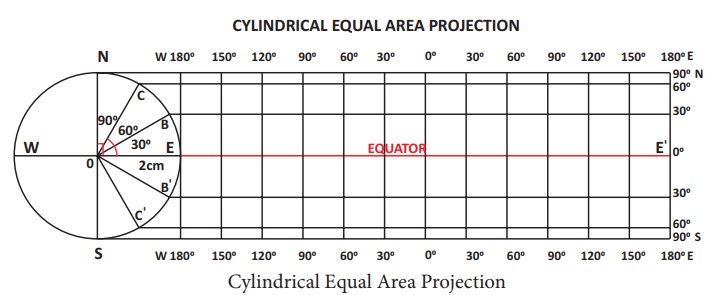
Cylindrical Equal Area Projection / Lambert’s Cylindrical Equal-area projection

Construction of Some selected Map Projections

Cylindrical Equal Area Projection / Lambert’s Cylindrical Equal-area projection

It is devised by JH Lambert in 1772. It is a normal perspective projection onto a cylinder tangent at the equator.

Properties of Cylindrical Equal Area Projection

* Parallels and meridians are straight lines.

* The meridians intersect parallels at right angles.

* The distance between parallels decreases toward the poles but meridians are equally spaced.

* The length of the equator on this projection is same as that on globe but other parallels are longer than corresponding parallels on globe. So, the scale is true along the equator but is exaggerated along other parallels.

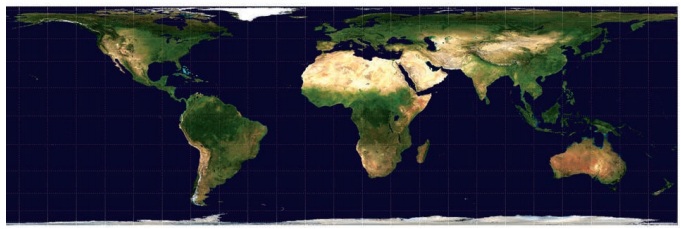
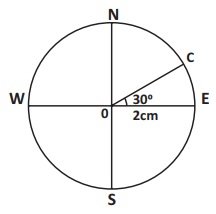
Example 1

Construct a cylindrical equal area projection for the whole globe with a reduced earth radius of 2 cm and the latitudinal and longitudinal interval 30°

Construction:

* Draw a circle of 2 cm radiuswith O as centre.

* Draw the equator (WE) and the Polar N-S axis.

* Mark the angles of 30°, 60° for both the hemispheres. And label it as B, C, B' and C' respectively.

* Extend the line WE to E’

* Divide the line EE’ into to 12 equal parts (360/30) with the distance of EB. This line represents the Equator.

* Through each point draw perpendiculars which represent the longitudes

* Draw parallel lines at N, C, B, B', C' and S equal to EE’ to represent 30°, 60° and 90° latitudes for both the hemispheres. Complete the projection as shown in Figure.

Cylindrical Equi –Distant Projection

This is a Projection on to a cylinder which is tangent to the equator. It is believed to be invented by Marinus of Tyre, about C.E. 100.

Properties of Cylindrical Equi-Distant Projection

* Poles are straight lines equal in length to the equator.

* Meridians are straight parallel lines, equally spaced and are half as long as the equator. All meridians are of same length therefore scale is true along all meridians

* Parallels are straight, equally spaced lines which are perpendicular to the meridians and are equal to the length of the equator.

* Length of the equator on the map is the same as that on the globe but the length of other parallels on map is more than the length of corresponding parallels on the globe. So the scale is true only along the Equator and not along other parallels.

* Distance between the parallels and meridians remain same throughout the map.

* Since the projection is neither equal area nor orthomorphic, maps on this projection are used for general purposes only.

Example 2

Construct a cylindrical equi-distant projection for the whole globe with a reduced earth radius of 2 cm and the latitudinal and longitudinal interval 30°.

Construction:

* Draw a circle of 2 cm radius with O as centre.

* Mark the angles of 30º northern hemisphere and label it as C.

* Draw a line AB long to represent the equator.

* Since the meridians are to be drawn at an interval of 30º divide AB into 360/30 i.e 12 equal parts with distance of EC.

* To draw meridians, erect perpendiculars on the points of divisions of AB. Take these perpendiculars equal to the length specified for a meridian and keep half of their length on either side of the equator.

* A meridian on a globe is subtended by180º. Since the parallels are to be drawn at an interval of 30º, divide the central meridian into 180/30 i.e. 6 parts.

* Through these points of divisions draw lines parallel to the equator. These lines will be parallels of latitude. Complete the projection as shown in Figure.

Polar Zenithal Projection

Polar Zenithal Equal area projection

This projection is invented by J.H Lambert in the year 1772. It is also known as Lambert’s Equal Area Projection.

* The pole is a point forming the centre of the projection and the parallels are concentric circles.

* The meridians are straight lines radiating from pole having correct angular distance between them.

* The meridians intersect the parallels at right angles.

The scale along the parallels increases away from the centre of the projection

* The decrease in the scale along meridians is in the same proportion in which there is an increase in the scale along the parallels away from the centre of the projection. Thus the projection is an equal area projection.

* Shapes are distorted away from the centre of the projection. Scale along the meridians is small and along the parallels is large so the shapes are compressed along the meridians but stretched along the parallels.

* Used for preparing political and distribution maps of Polar Regions. It can also be used for preparing general purpose maps of large areas in Northern Hemisphere.

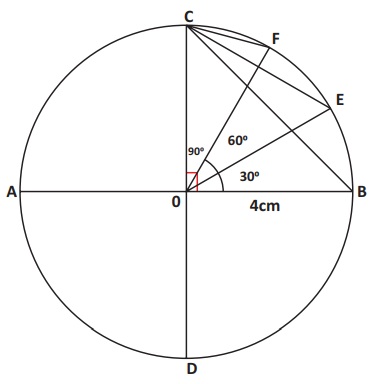
Example 3

Construct a Polar zenithal equal area projection for the whole globe with a reduced earth radius of 4 cm and the latitudinal and longitudinal interval 30°

Steps of construction:

* Draw a circle with radius equal to 4 cm representing a globe. Let CD and AB be the polar and equatorial diameters respectively which intersect each other at right angles at O, the centre of the circle.

* Draw radii OE, OF, OC, making angles of, 30°, 60° and 90° respectively with OB. Join CB, CE, and CF by straight lines.

* With radius equal to CF as centre draw a circle. The point represent 900 parallel and mark it as N. This circle represents 60° parallel. Similarly with centre N and radii equal to CE and CB draw circles to represent the parallels of 30° and 0° respectively.

* Using protractor, draw other radii at 30° interval to represent other meridians.

* Complete the projection as shown in Figure.

Polar Zenithal Equi-distant Projection

Properties of Polar Zenithal Equi distant Projection

* The pole is a point forming the centre of the projection and the parallels are concentric circles.

* The meridians are straight lines radiating from pole having correct angular distance between them.

* The meridians intersect the parallels at right angles.

* The spacing between the parallels represent true distances, therefore the scale along the meridians is correct.

* The scale along the parallels increases away from the centre of the projection.

* It is used for preparing maps of polar areas for general purposes.

Example 4

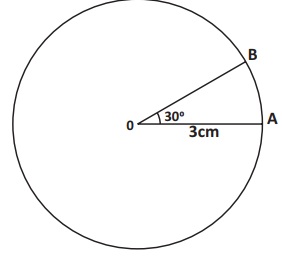
Construct a Polar zenithal equi-distant projection for the whole globe with a reduced earth radius of 3cm and the latitudinal and longitudinal interval 30°.

Steps of construction:

* Draw a circle with radius equal to 3cm representing a globe with O as centre.

* Mark the angle of 30° and label it as AOB.

* With radius equal to AB as centre draw a circle with centre N.

* Let CD and AB be the polar and equatorial diameters respectively which intersect each other at right angles at O, the centre of the circle.

* The number of intervals will be 90/30 = 3.

* Draw 3 concentric circles with N as centre. Mark the meridians radiating from the centre N.

* Using protractor, draw other radii at 30° interval to represent other meridians.

* Complete the projection as shown in Figure.