Classification of Map Projections

Classification of Map Projections

Map projections are classified on the following criteria:

* Method of construction

* Development surface used

* Projection properties

* Position of light source

Classification based on Methods of Construction

Given below are the projections that are based on the method of construction:

a).Perspective Projections: These projections are made with the help of shadow cast from an illuminated globe on to a developable surface.

b). Non Perspective Projections: A developable surface is only assumed to be covering the globe and the construction of projections is done using mathematical calculations.

Classification based on Developable Surface used

The three basic projections are based on the types of developable surface. They are:

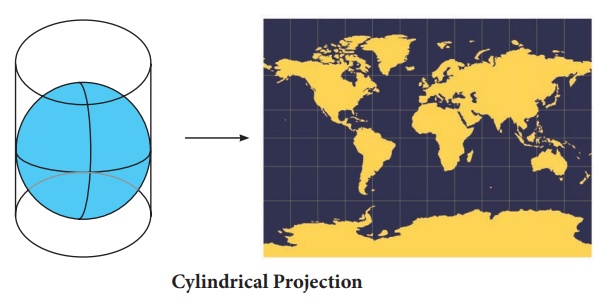
1 Cylindrical Projection

* It can be visualized as a cylinder wrapped around the globe.

* The longitudes (meridians) and latitudes (parallels) appear as straight lines.

* Length of equator on the cylinder is equal to the length of the equator, therefore, it is suitable for showing equatorial regions.

Normal: when a cylinder has line of tangency to the equator. It includes Equirectangular Projection, the Mercator projection, Lambert's Cylindrical Equal Area, Gall's Stereographic Cylindrical, and Miller cylindrical projection.

Transverse: when cylinder has line of tangency to the meridian. It includes the Cassini Projection, Transverse Mercator, Transverse cylindrical Equal Area Projection, and Modified Transverse Mercator.

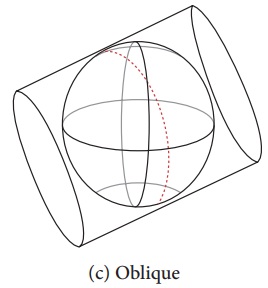
Oblique: when cylinder has line of tangency to another point on the globe. It only consists of the Oblique Mercator projection.

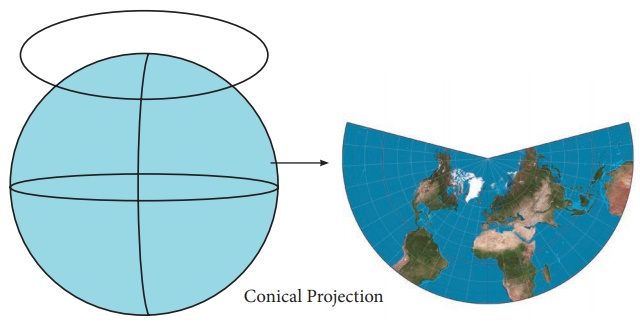
2. Conical Projection

* It can be visualized as a cone placed on the globe, tangent to it at some parallel.

* After projecting the graticule on to the cone, the cone is cut along one of the meridian and unfolded. Parallels appear as arcs with a pole and meridians as straight lines that converge to the same point.

* It can represent only one hemisphere, at a time, northern or southern hemisphere.

* It is suitable for representing middle latitudes.

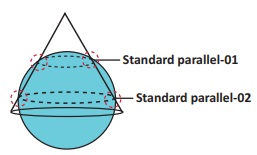
Conical projection is divided into two. They are

Tangent: when the cone is tangent to only one of the parallel.

Secant: when the cone is not big enough to cover the curvature of earth, it intersects the earth twice at two parallels.

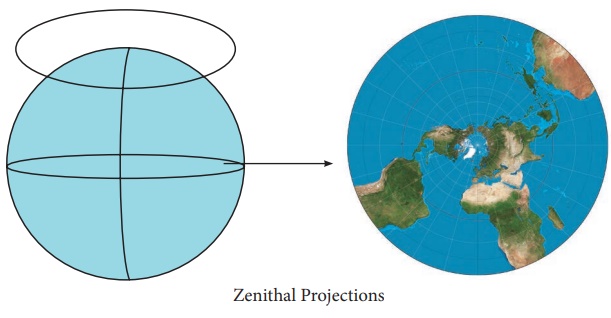
3. Azimuthal /Zenithal Projection

* It can be visualized as a flat sheet of paper tangent to any point on the globe

* The sheet will have the tangent point as the centre of the circular map, where meridians passing through the centre are straight line and the parallels are seen as concentric circle.

* Suitable for showing polar areas

Aspects of zenithal projection:

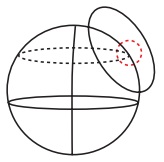
Equatorial zenithal: When the plane is tangent to a point on the equator.

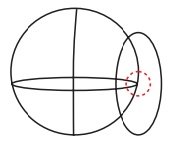
Oblique zenithal: when the plane is tangent to a point between a pole and the equator.

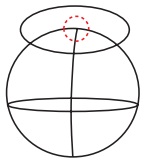
Polar zenithal: when the plane is tangent to one of the poles.

According to properties, map projections can be classified as:

Equal area projection: It is also known as homolographic projections. The areas of different parts of earth are correctly represented by such projections.

True shape projection: It is also known as orthomorphic projections. The shapes of different parts of earth are correctly represented on these projections.

True scale or equidistant projections: Projections that maintain correct scale are called true scale projections. However, no projection can maintain the correct scale throughout. Correct scale can only be maintained along some parallels or meridians.

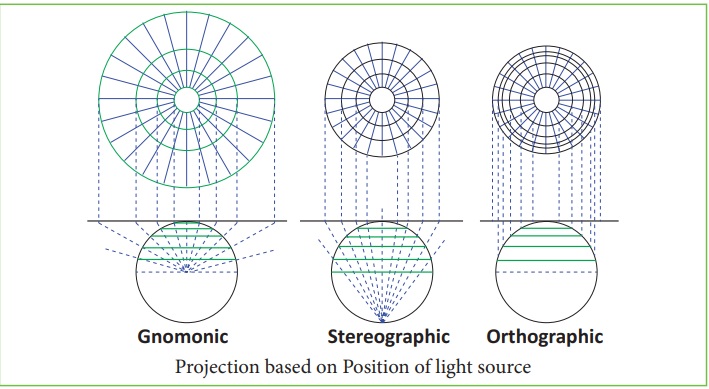
Classification based on Position of light source

Placing light source illuminating the globe at different positions results in the development of different projections. These projections are

Gnomonic projection: when the source of light is placed at the centre of the globe

Stereographic Projection: when the source of light is placed at the periphery of the globe, diametrically opposite to the point at which developable surface touches the globe.

Orthographic Projection: when the source of light is placed at infinity from the globe opposite to the point at which developable surface touches the globe.