Chapter: Civil : Railway Airport Harbour Engineering : Railway Engineering : Track Junctions and Simple Track Layouts
Crossover Between Two Parallel Railway Tracks with an Intermediate Straight Length
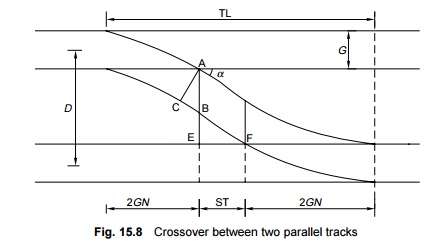
Crossover Between Two
Parallel Tracks with an Intermediate Straight Length
The crossover between two parallel tracks with an intermediate
straight length can be designed by applying any one of two methods.
Coles
design
Coles design is a simple layout. In this case, two parallel
tracks at a distance D from each other are connected by a crossover with
a small length of the straight portion of the track lying between the two
theoretical noses of the crossing. The straight portion of the track (ST) can
be calculated using the formula
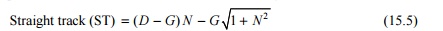
where G is the gauge of the track and N is the
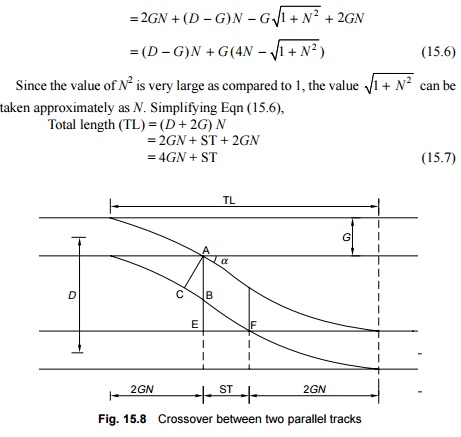
number of the crossing. The overall length (OL) of the crossover from the
tangent point of one track to the tangent point of the other track is found by
adding the lengths of the curve leads of the two turnouts and the length of the
straight portion in between the two TNC (Fig. 15.8).
Overall length = OL of one turnout + ST + OL of other turnout
Example 15.1 A 1 in 8.5 crossover
exists between two BG parallel tracks with their centres 5 m apart. Find
the length of the straight track and the overall length of the crossover. Use
Coles method. Given D = 5 m, N = 8.5, G =1.676 m.
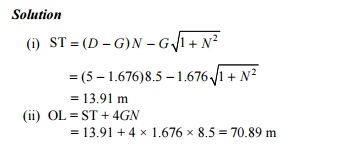
Example 15.2 A crossover is laid
between two BG straight tracks placed at a distance of 5 m c/c.
Calculate the (i) overall length, (ii) radius of the curved lead, (iii) lead
distance. Heel divergence of 1 in 12 crossing = 133 mm.

IRS
design
In IRS design, the distance from the TNC measured along the
straight track is given by the formula
ST = ( D - G - G
sec a ) cota
On simplification
ST = D cot a - G cot a/2
where ST is the distance from TNC to TNC along the straight
track, D is the distance from centre to centre of two tracks, G
is the gauge, and a is the
angle of crossing.
Similarly, the distance from TNC to TNC along the crossover is
given by the
formula (Fig. 15.8)
CF = (D - G - G
seca ) coseca + G tana
where CF is the distance from TNC to TNC along the crossover, D
is the distance from centre to centre of two tracks, G is the gauge, and
a is the angle of crossing.
Example 15.3 A 1 in 12 crossover of IRS
type is laid between two BG parallel tracks with their centres 5 m
apart. Calculate ST and the distance from TNC to TNC along the crossover.
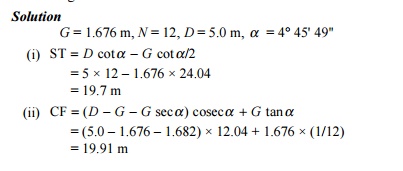
Related Topics