Chapter: Civil : Prestressed Concrete Structures : composite construction
Concrete Structures: Horizontal Shear
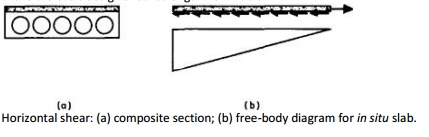
HORIZONTAL SHEAR
The composite behaviour of the precast beam and in
situ slab is only effective if the horizontal shear stresses at the interface
between the two regions can be resisted. For shallow members, such as that
shown in Fig. 10.3, there is usually no mechanical key between the two types of
concrete, and reliance is made on the friction developed between the contact
surfaces. For deeper sections, mechanical shear connectors in the form of links
projecting from the beam are used, which provide a much better shear
connection. The determination of the horizontal shear resistance is based on the
ultimate limit state, and if this condition is satisfied it may be assumed that
satisfactory horizontal shear resistance is provided at the serviceability
limit state. A simply supported composite section carrying a uniformly
distributed load is shown in Fig. 10.8(a) and the free-body diagram for half
the length of the in situ slab is shown in Fig. 10.8(b). At the simply
supported end there must be zero force in the slab, while the maximum force
occurs at the midspan. The distribution of shear forces on the underside of the
slab is also shown in Fig. 10.8(b), being zero at midspan and reaching a
maximum at the support. This behaviour is similar to that in an elastic beam,
where the vertical and horizontal shear stresses increase towards the support
for a uniformly distributed load.
The following expression is given in Part 1-3 of EC2
for the horizontal shear stress, where ß is the ratio of the longitudinal force
in the slab to the total longitudinal force, given by Msd/z, both calculated
for a given section; Vsd is the transverse ultimate shear force; z is the lever
arm; and bj is the width of the interface.
The design shear resistance for horizontal joints with
vertical shear reinforcement is given by
?Rdj=kT?Rd+??N+0.87 fyk? ??0.33 vfck,
where kT is a coefficient with kT=0 if the joint is
subjected to tension;
?Rd is the basic design shear strength from Table
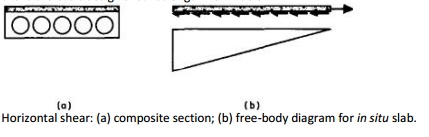
Horizontal shear: (a) composite section; (b) free-body
diagram for in situ slab.
DIFFERENTIAL MOVEMENTS
The fact that the slab of a composite member is
usually cast at a much later stage than the beam means that most of the
time-dependent effects of shrinkage of the slab take place with the section
acting compositely. Most of the shrinkage of the beam will already have occurred
by the time the slab is in place, and the movement due to the shrinkage of the
slab will induce stresses throughout the whole of the composite section. The
water content of the slab concrete is often higher than that of the beam, since
a lower strength is required, and this aggravates the problem of differential
shrinkage. These extra stresses, which occur even under zero applied load, are
not insignificant and should be considered in design. Both the slab and beam
undergo creep deformations under load and, although some of the creep
deformations in the beam may have taken place before casting of the slab, the
level of compressive stress is higher in the beam, and so the creep
deformations are larger.
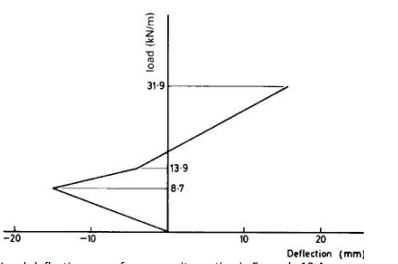
Load-deflection curve for composite section in Example
10.4.
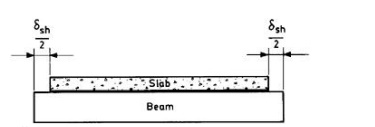
Differential movements.
composite section which tend to reduce those set up by
differential shrinkage. A problem which is encountered, particularly in
connection with bridge decks, is that of varying temperature across a composite
section, although this may still be a problem in composite members used as roof
structures. The hotter upper surface tends to expand more than the cooler lower
surface and stresses are induced throughout the composite section.
A method for determining the stresses due to
differential shrinkage will now be outlined, and this can be adapted to find
the stresses due to differential creep and temperature movements. Consider a
composite member as shown in Fig. 10.13, where the slab is shown to have a free
shrinkage movement of ?sh relative to the beam. In reality this movement is
restrained by the shear forces which are set up between the slab and beam,
putting the slab into tension and the beam into compression. The magnitude of
the tensile force in the slab is given by
T=?shAc,slabEc,slab,
where Ac,slab and Ec,slab are the cross-sectional area
and modulus of elasticity of the slab, respectively, and ?sh is the free
shrinkage strain of the slab concrete.
The compressive force in the beam must be numerically
equal to this tensile force. In addition to the direct stresses described
above, bending stresses are also introduced by restraint of the free
differential shrinkage. In order to determine these stresses, the free bodies
of the slab and beam are considered, as shown in Fig. 10.14. Initially, the
slab can be regarded as having a force T applied through its centroid, so that
its length is equal to that of the beam. There must be no net external force on
the composite member due to differential shrinkage alone, so a pair of equal
and opposite compressive forces must be applied to maintain equilibrium.
However, these compressive forces act on the composite section and induce a
bending moment at the ends of the member of Internal stress resultants due to
differential movements.

Stresses due to differential movements.
Related Topics