Circuits for Arithmetic operations

CIRCUITS FOR ARITHMETIC OPERATIONS

Arithmetic circuits are the ones which perform arithmetic operations like addition, subtraction, multiplication, division, parity calculation. Most of the time, designing these circuits is the same as designing mux, encoders and decoders.

1.                 Adders

Adders are the basic building blocks of all arithmetic circuits; adders add two binary numbers and give out sum and carry as output. Basically we have two types of adders.

·       Half Adder.

·                    Full Adder.

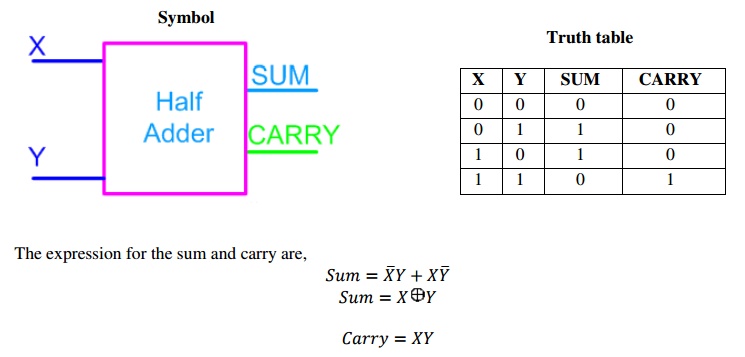
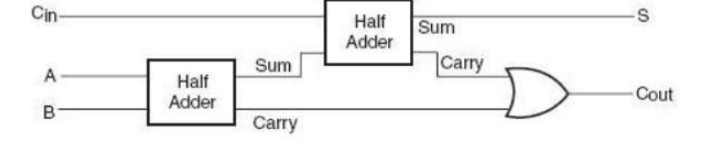
ü    Half Adder

A half-adder is an arithmetic circuit block that can be used to add two bits. Such a circuit thus has two inputs that represent the two bits to be added and two outputs, with one producing the SUM output and the other producing the CARRY.

Adding two single-bit binary values X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and thus the circuit to realize it is called a half adder.

ü    Full Adder

A full adder circuit is an arithmetic circuit block that can be used to add three bits to produce a SUM and a CARRY output. Such a building block becomes a necessity when it comes to adding binary numbers with a large number of bits. The full adder circuit overcomes the limitation of the half-adder, which can be used to add two bits only.

Full adder takes a three-bits input. Adding two single-bit binary values X, Y with a carry input bit C-in produces a sum bit S and a carry out C.

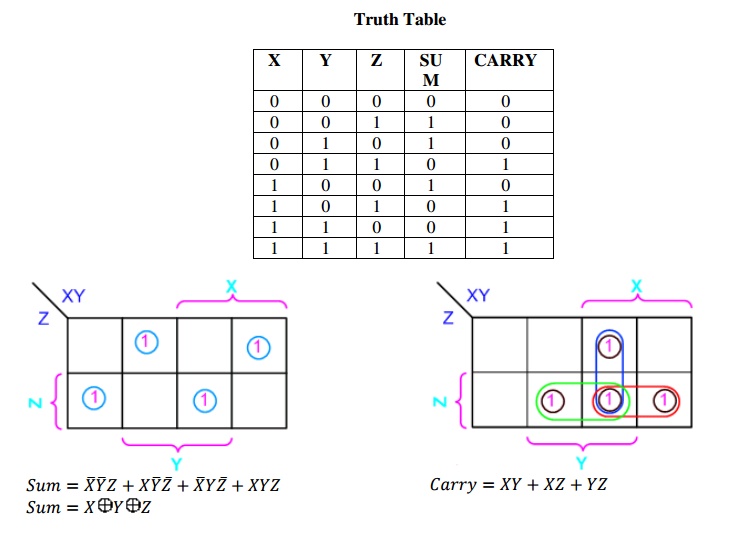
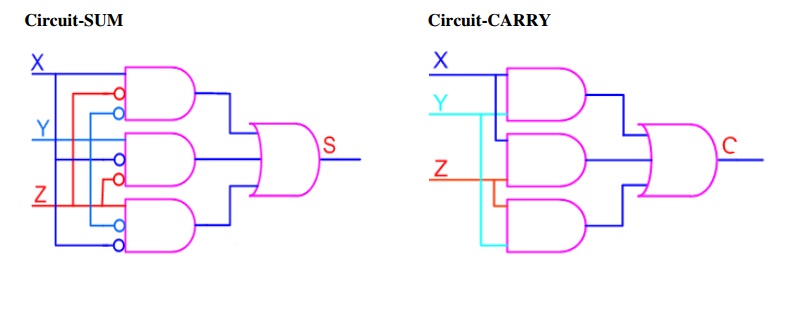
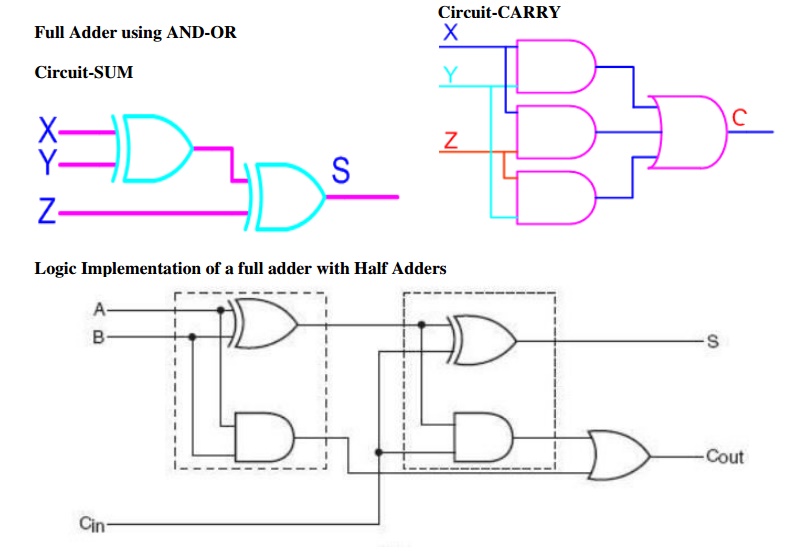
Full Adder using AND-OR

The below implementation shows implementing the full adder with AND-OR gates, instead of using XOR gates. The basis of the circuit below is from the above K-map

Circuit-SUM        Circuit-CARRY

ü n-bit Carry Ripple Adder

An n-bit adder used to add two n-bit binary numbers can be built by connecting n full adders in series. Each full adder represents a bit position j (from 0 to n-1).

Each carry out C-out from a full adder at position j is connected to the carry in C-in of the full adder at higher position j+1. The output of a full adder at position j is given by:

Sj= Xj  Yj  Cj

Cj+1 = Xj . Yj + Xj . Cj + Y . Cj

In the expression of the sum Cj must be generated by the full adder at lower position j. The propagation delay in each full adder to produce the carry is equal to two gate delays = 2 D Since the generation of the sum requires the propagation of the carry from the lowest position to the highest position , the total propagation delay of the adder is approximately:

Total Propagation delay = 2 nD

4-bit Carry Ripple Adder

Adds two 4-bit numbers:

X = X3 X2 X1 X0

Y = Y3 Y2 Y1 Y0

Producing the sum S = S3 S2 S1 S0, C-out = C4 from the most significant position j=3 Total Propagation delay = 2 nD = 8D or 8 gate delays

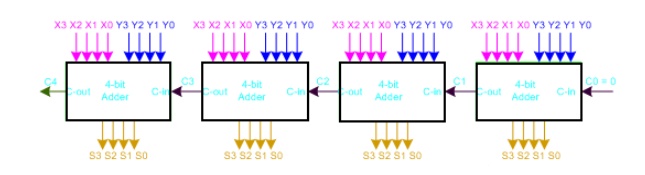
Larger Adder

Example: 16-bit adder using 4 4-bit adders. Adds two 16-bit inputs X (bits X0 to X15), Y (bits Y0 to Y15) producing a 16-bit Sum S (bits S0 to S15) and a carry out C16 from the most significant position. Propagation delay for 16-bit adder = 4 x propagation delay of 4-bit adder

= 4 x 2 nD = 4 x 8D = 32 D or 32 gate delays

ü     Carry Look-Ahead Adder

The delay generated by an N-bit adder is proportional to the length N of the two numbers X and Y that are added because the carry signals have to propagate from one full-adder to the next. For large values of N, the delay becomes unacceptably large so that a special solution needs to be adopted to accelerate the calculation of the carry bits. This solution involves a "look-ahead carry generator" which is a block that simultaneously calculates all the carry bits involved. Once these bits are available to the rest of the circuit, each individual three-bit addition (X_i+Y_i+carry-in_i) is implemented by a simple 3-input XOR gate. The design of the look-ahead carry generator involves two Boolean functions named Generate and Propagate. For each input bits pair these functions are defined as: Gi = Xi . Yi & Pi = Xi + Yi

The carry bit c-out(i) generated when adding two bits Xi and Yi is '1' if the corresponding function Gi is '1' or if the c-out(i-1)='1' and the function Pi = '1' simultaneously. In the first case, the carry bit is activated by the local conditions (the values of Xi and Yi). In the second, the carry bit is received from the less significant elementary addition and is propagated further to the more significant elementary addition. Therefore, the carry_out bit corresponding to a pair of bits Xi and Yi is calculated according to the equation:

carry_out(i) = Gi + Pi.carry_in(i-1)

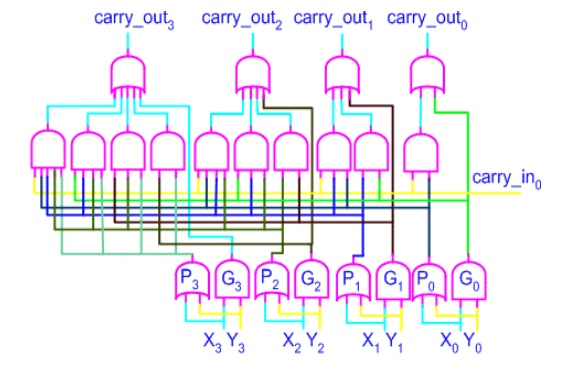
For a four-bit adder the carry-outs are calculated as follows

carry_out0 = G0 + P0 . carry_in0

carry_out1 = G1 + P1 . carry_out0 = G1 + P1G0 + P1P0 . carry_in0 carry_out2 = G2 + P2G1 + P2P1G0 + P2P1P0 . carry_in0

carry_out3 = G3 + P3G2 + P3P2G1 + P3P2P1G0 + P3P2P1 . carry_in0

The set of equations above are implemented by the circuit below and a complete adder with a look-ahead carry generator is next. The input signals need to propagate through a maximum of 4 logic gate in such an adder as opposed to 8 and 12 logic gates in its counterparts illustrated earlier.

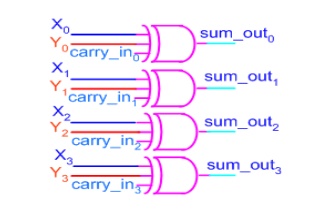
Sums can be calculated from the following equations, where carry_out is taken from the carry calculated in the above circuit.

sum_out0 = X 0 Y0 carry_out0 sum_out1 = X 1 Y1 carry_out1 sum_out2 = X 2 Y2 carry_out2 sum_out3 = X 3 Y3 carry_out3

ü    BCD Adder

BCD addition is the same as binary addition with a bit of variation: whenever a sum is greater than 1001, it is not a valid BCD number, so we add 0110 to it, to do the correction. This will produce a carry, which is added to the next BCD position.

·                    Add the two 4-bit BCD code inputs.

· Determine if the sum of this addition is greater than 1001; if yes, then add 0110 to this sum and generate a carry to the next decimal position

2. Subtractor

Subtractor circuits take two binary numbers as input and subtract one binary number input from the other

binary number input. Similar to adders, it gives out two outputs, difference and borrow (carry-in the case

of Adder). The BORROW output here specifies whether a ‗1‘ has been borrowed to theperform subtraction.

There are two types of subtractors,

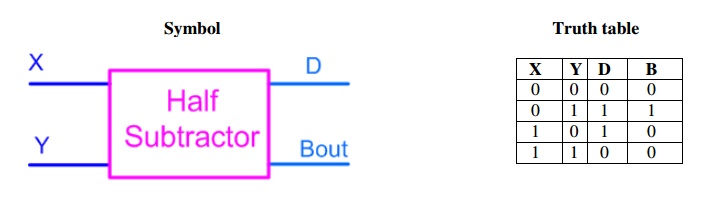
ü    Half Subtractor

The half-subtractor is a combinational circuit which is used to perform subtraction of two bits. It has two inputs, X (minuend) and Y (subtrahend) and two outputs D (difference) and B (borrow). The logic symbol and truth table are shown below.

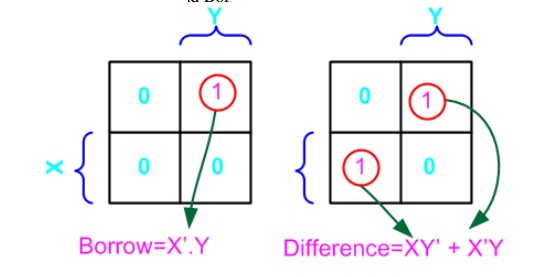
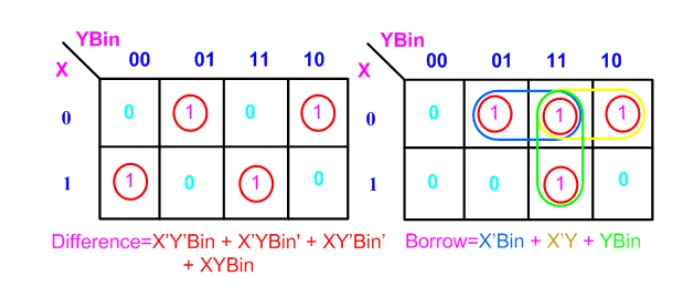
From the above table we can draw the K-map as shown below for "difference" and "borrow". The Boolean expression for the difference and Borrow can be written.

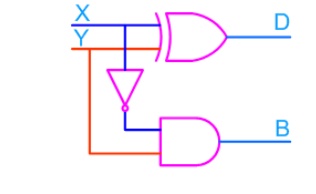
From the equation we can draw the half-subtractor as shown in the figure below.

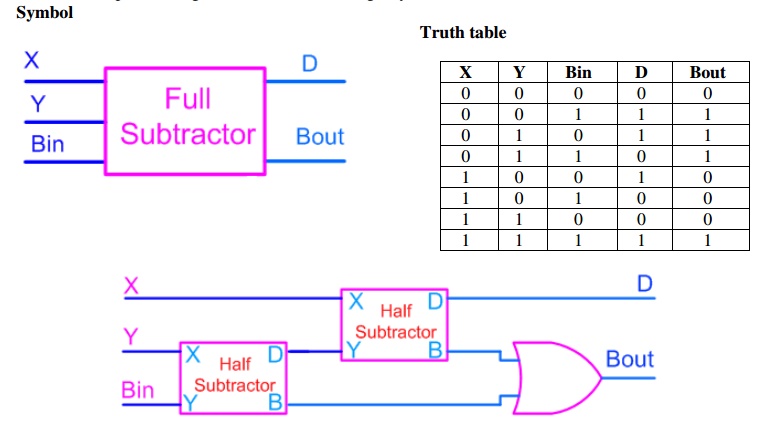
ü Full Subtractor

A  full  subtractor  is  a  combinational  circuit  that  performs  subtraction  involving  three  bits,  namely

minuend, subtrahend, and borrow-in. There are two outputs, namely the DIFFERENCE output D and the BORROW output Bo. The BORROW output bit tells whether the minuend bit needs to borrow a

from the next possible higher minuend bit. The logic symbol and truth table are shown below.

Symbol

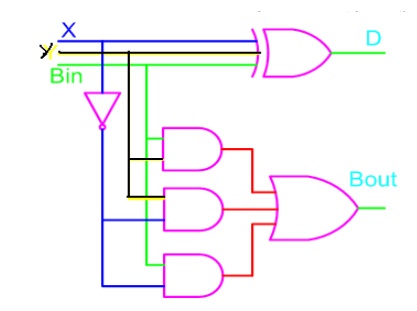
From the above expression, we can draw the circuit below. If you look carefully, you will see that a full-subtractor circuit is more or less same as a full-adder with slight modification.

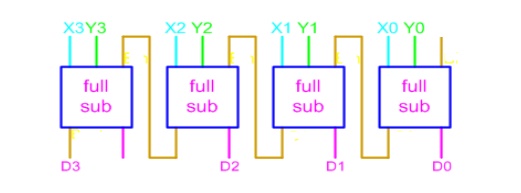
ü    Parallel Binary Subtractor

Parallel binary subtractor can be implemented by cascading several full-subtractors. Implementation and associated problems are those of a parallel binary adder, seen before in parallel binary adder section.

Below is the block level representation of a 4-bit parallel binary subtractor, which subtracts 4-bit Y3Y2Y1Y0 from 4-bit X3X2X1X0. It has 4-bit difference output D3D2D1D0 with borrow output Bout.

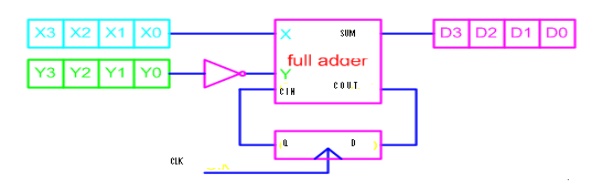
ü   Serial Binary Subtracter

A serial subtracter can be obtained by converting the serial adder using the 2's complement system. The subtrahend is stored in the Y register and must be 2's complemented before it is added to the minuend stored in the X register. The circuit for a 4-bit serial subtracter using full-adder is shown in the figure below.

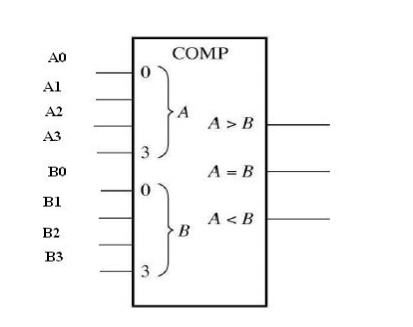
ü    Comparators

It  is a combinational circuit that compares two numbers and determine their relative magnitude. The output of comparator is usually 3 binary variables indicating:

A<B, A=B, A>B

1-bit comparator: Let’sbegin with 1 bit comparator and from the name we can easily make out that this circuit would be used to compare 1 bit binary numbers.

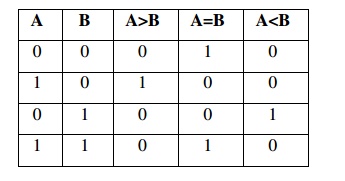
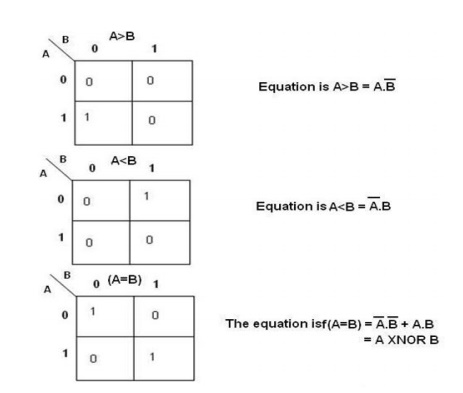
For a 2-bit comparator we have four inputs A1A0 and B1B0 and three output E ( is 1 if two numbers are equal) G (is 1 when A > B) and L (is 1 when A < B) If we use truth table and K-map the result is

The comparison process of two positive numbers X and Y is performed in a bit-by-bit manner starting with the most significant bit:

If the most significant bits are Xn='1' and Yn='0' then number X is larger than Y.

·                       If Xn='0' and Yn='1' then number X is smaller than Y.

·                       If Xn=Yn then no decision can be taken about X and Y based only on these two bits.

If the most significant bits are equal then the result of the comparison is determined by the less significant bits Xn-1 and Yn-1. If these bits are equal as well, the process continues with the next pair of bits. If all bits are equal then the two numbers are equal.

4-bit comparator:

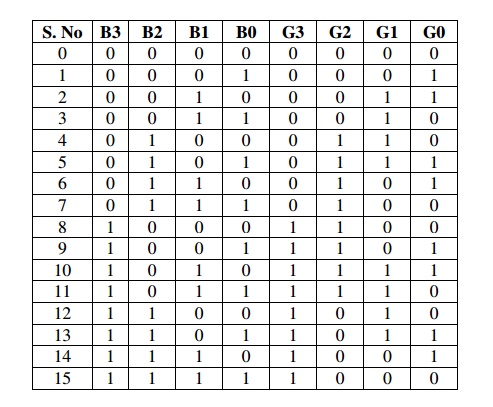
CODE CONVERSION-

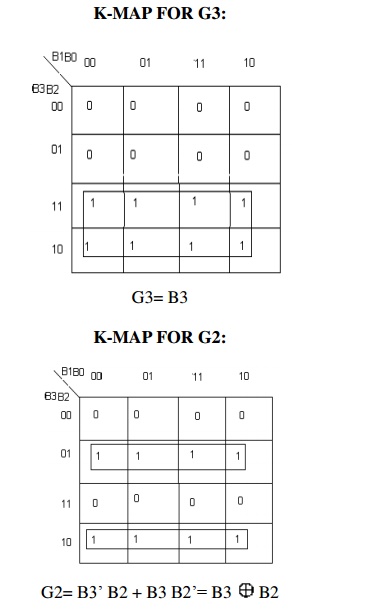
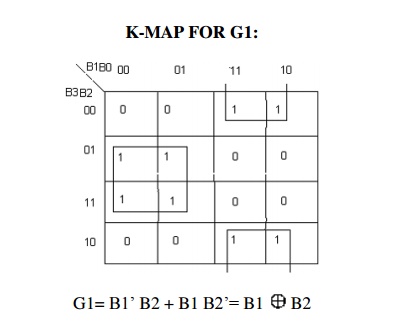
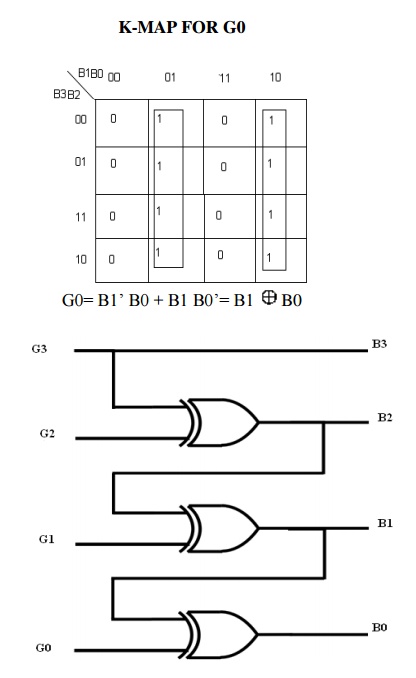
Binary to Gray converter

Truth Table

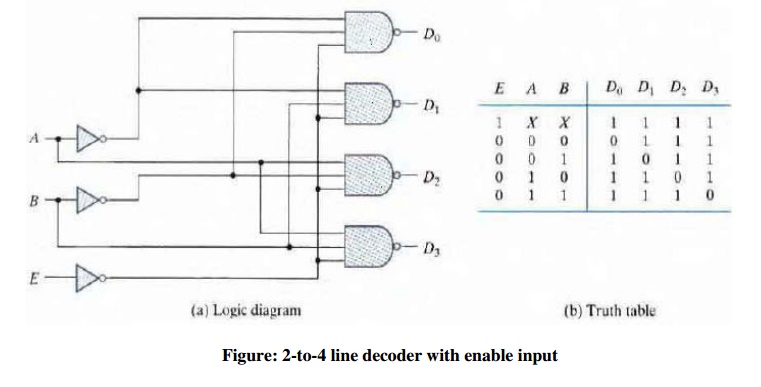
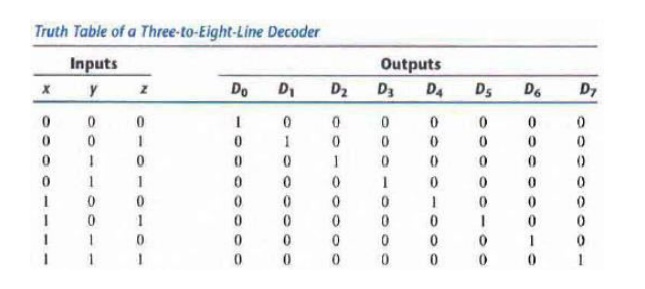
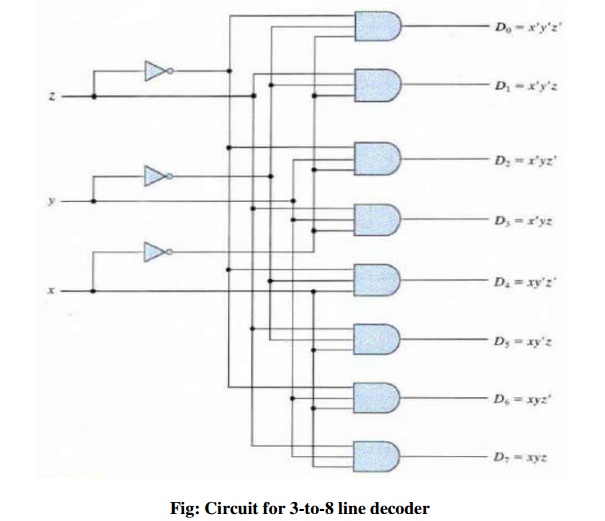
DECODERS

A decoder circuit can be used to implement AND-OR circuit SOP Boolean expression when decoder active state output is 1 and inactive 0 .

• Number of binary inputs = n

• Number of binary outputs = 2n = Maximumumber n of minterms, where n is the number of literals in F

• Its outputs reflect the-Mini terms with one term each at each of the output

ENCODERS

An encoder is a circuit that converts the binary information from one form to another. Gives a unique combination of outputs according to the information at a unique input at one-line (or at multiple lines).

Action of a one active line input encoder is opposite of that of a one active line output decoder. An encoder, which has multi-lines as the active inputs, is also called ‘priority encoder’. Encoder

differentiated from decoder by greater number of inputs than outputs compared to the decoder. The priority encoder includes a priority function.

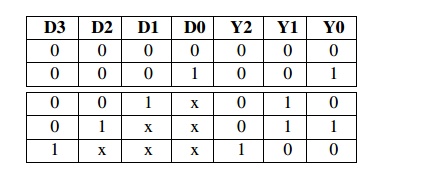
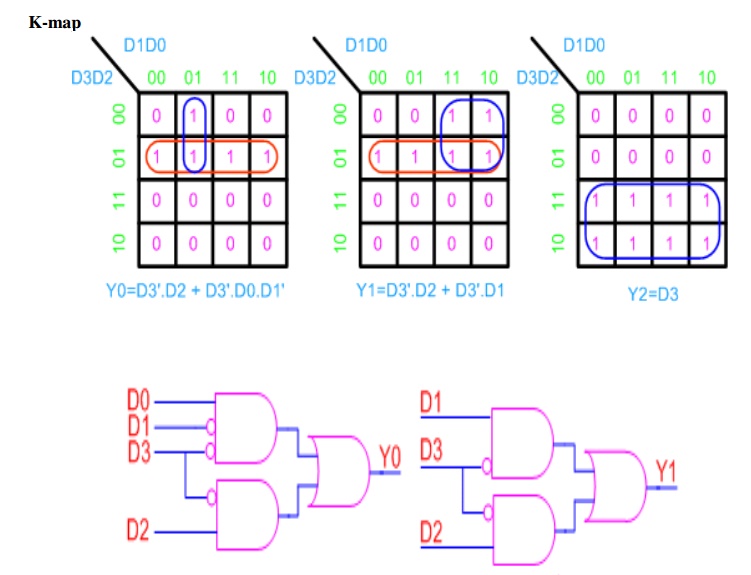
4to3 Priority Encoder-The truth table of a 4-input priority encoder is as shown below. The input D3 has the highest priority, D2 has next highest priority, D0 has the lowest priority. This means output Y2 and Y1 are 0 only when none of the inputs D1, D2, D3 are high and only D0 is high. A 4 to 3 encoder consists of four inputs and three outputs, truth table and symbols of which is shown below.

Truth Table

MULTIPLEXERS

Many tasks in communications, control, and computer systems can be performed by combinational logic circuits. When a circuit has been designed to perform some task in one application, it often finds use in a different application as well.

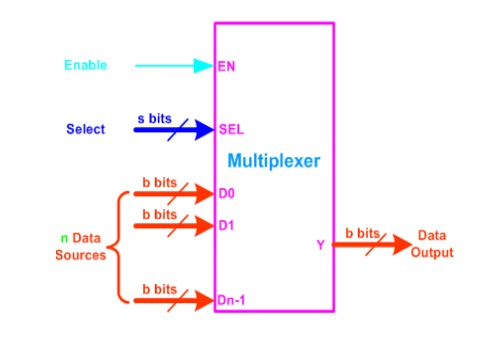
A multiplexer (MUX) is a digital switch which connects data from one of n sources to the output. A number of select inputs determine which data source is connected to the output. The block diagram of MUX with n data sources of b bits wide and s bits wide select line is shown in below figure.

Example - 2x1 MUX

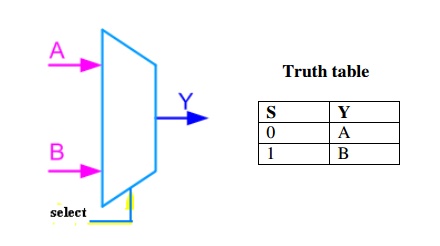
A 2 to 1 line multiplexer is shown in figure below, each 2 input lines A to B is applied to one input of an AND gate. Selection lines S are decoded to select a particular AND gate. The truth table for the 2:1 mux is given in the table below.

Design of a 2:1 Mux

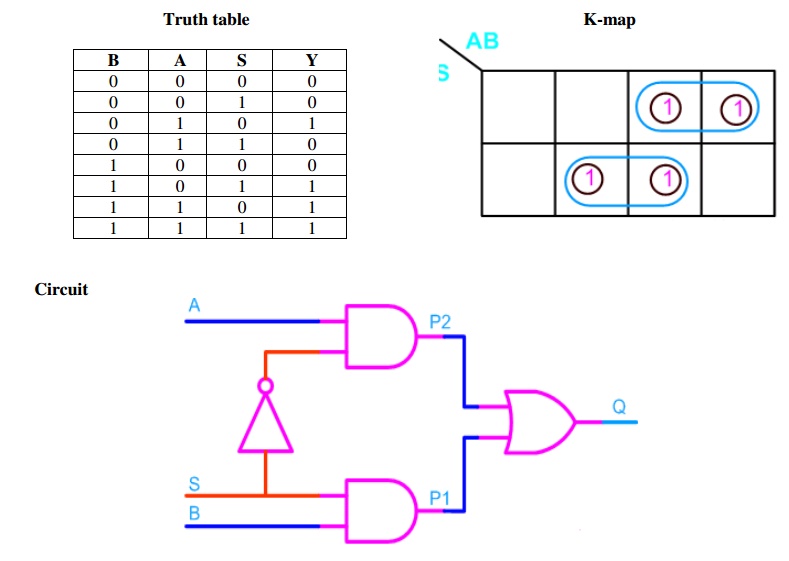
To derive the gate level implementation of 2:1 mux we need to have truth table as shown in figure. And once we have the truth table, we can draw the K-map as shown in figure for all the cases when Y is equal to '1'.

Combining the two 1' as shown in figure, we can drive the output y as shown below

Y = A.S' + B.S

Example : 4:1 MUX

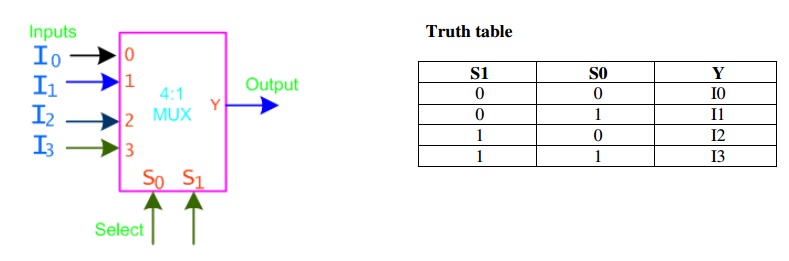
A 4 to 1 line multiplexer is shown in figure below, each of 4 input lines I0 to I3 is applied to one input of an AND gate. Selection lines S0 and S1 are decoded to select a particular AND gate. The truth table for the 4:1 mux is given in the table below.

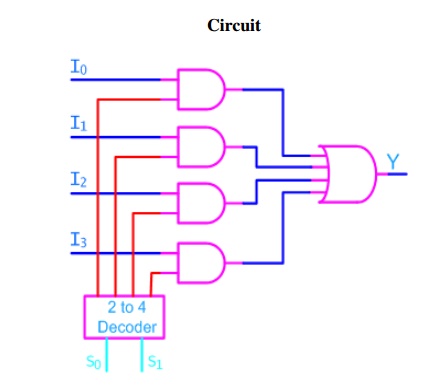
DEMULTIPLEXERS

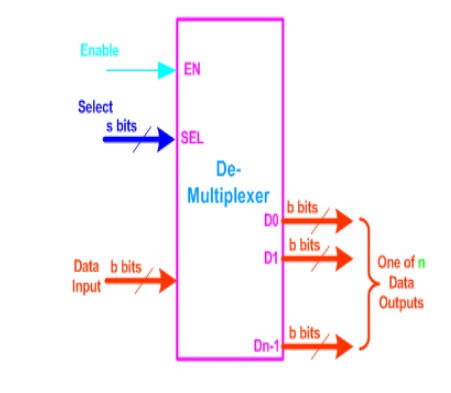
They are digital switches which connect data from one input source to one of n outputs. Usually implemented by using n-to-2n binary decoders where the decoder enable line is used for data input of the de-multiplexer.

The figure below shows a de-multiplexer block diagram which has got s-bits-wide select input, one b-bits-wide data input and n b-bits-wide outputs.

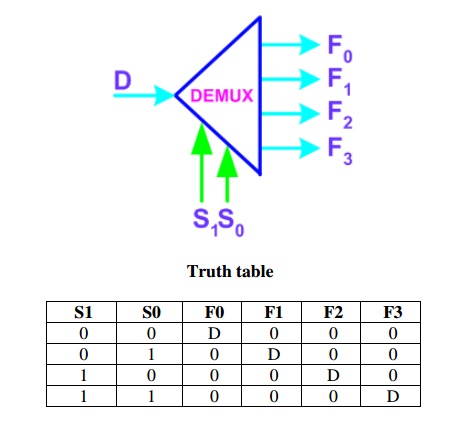
Example: 1-to-4 De-multiplexer

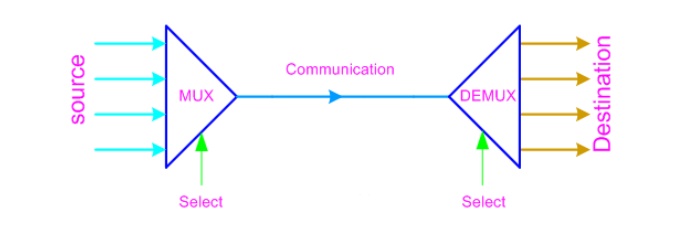
Mux- Demux: Application Example

This enables sharing a single communication line among a number of devices. At any time, only one source and one destination can use the communication line.

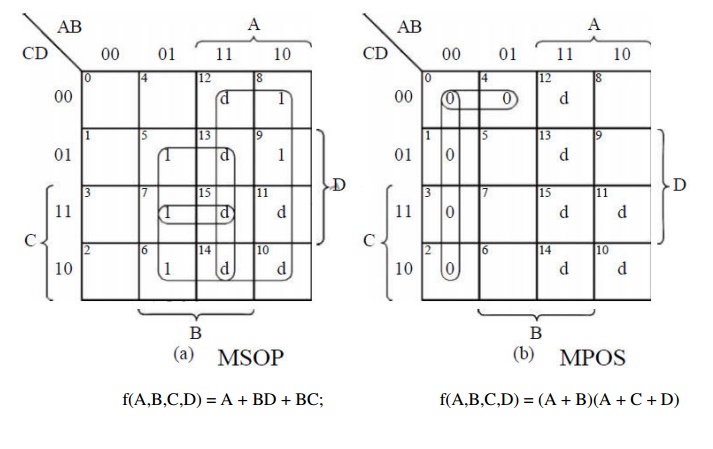
Example: Design a circuit to distinguish BCD digits ≥ 5 from those < 5.