Arithmetic Operations: Division

DIVISION

The reciprocal operation of multiply is divide, an operation that is even less frequent and even more quirky.

It even offers the opportunity to perform a mathematically invalid operation: dividing by 0. The example is dividing 1,001,010 by 1000. The two operands (dividend and divisor) and the result (quotient) of divide are accompanied by a second result called the remainder. Here is another way to express the relationship between the components:

Fig. 2.8 First version of the Division hardware

Dividend = Quotient *  Divisor + Remainder

where the remainder is smaller than the divisor. Infrequently, programs use the divide instruction just to get the remainder, ignoring the quotient. The basic grammar school division algorithm tries to see how big a number can be subtracted, creating a digit of the quotient on each attempt. Binary numbers contain only 0 or 1, so binary division is restricted to these two choices, thereby simplifying binary division. If both the dividend and divisor are positive and hence the quotient and the remainder are nonnegative. The division operands and both results are 32-bit values.

A Division Algorithm and Hardware

Initially, the 32-bit Quotient register set to 0. Each iteration of the algorithm needs to move the divisor to the right one digit, start with the divisor placed in the left half of the 64-bit Divisor register and shift it right 1 bit each step to align it with the dividend. The Remainder register is initialized with the dividend. Figure shows three steps of the first division algorithm.

Unlike a human, the computer isn’t smart enough to know in advance whether the divisor is smaller than the dividend. It must first subtract the divisor in step 1; If the result is positive, the divisor was smaller or equal to the dividend, so generate a 1 in the quotient (step 2a). If the result is negative, the next step is to restore the original value by adding the divisor back to the remainder and generate a 0 in the quotient (step 2b). The divisor is shifted right and then iterate again. The remainder and quotient will be found in their namesake registers after the iterations are complete.

The following figure shows three steps of the first division algorithm. Unlike a human, the computer isn’t smart enough to know in advance whether the divisor is smaller than the

dividend.

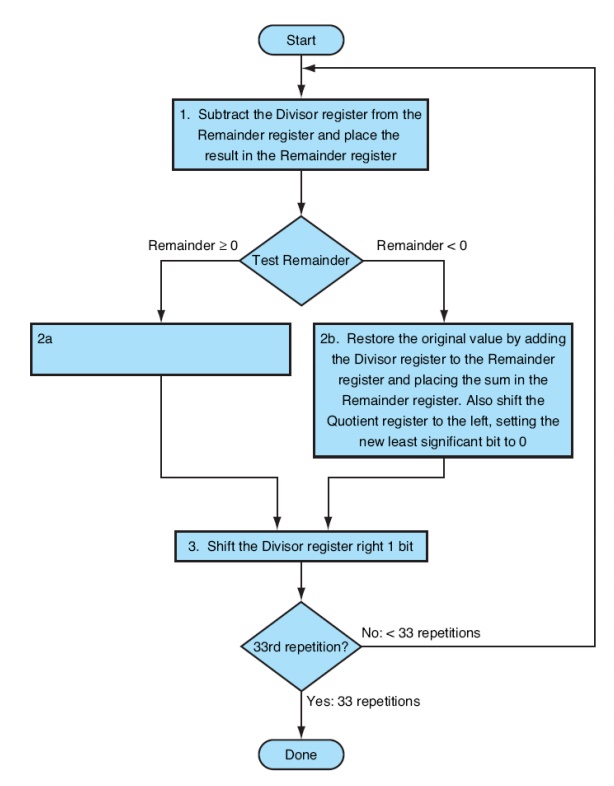
Fig. 2.9 Division Algorithm

It must first subtract the divisor in step 1; remember that this is how we performed the comparison in the set on less than instruction. If the result is positive, the divisor was smaller or equal to the dividend, so we generate a 1 in the quotient (step 2a). If the result is negative, the next step is to restore the original value by adding the divisor back to the remainder and generate a 0 in the quotient (step 2b). The divisor is shifted right and then we iterate again. The remainder and quotient will be found in their namesake registers after the iterations are complete.

Using a 4-bit version of the algorithm to save pages, let’s try dividing 7₁₀ by 2₁₀, or 0000 0111₂ by 0010₂.

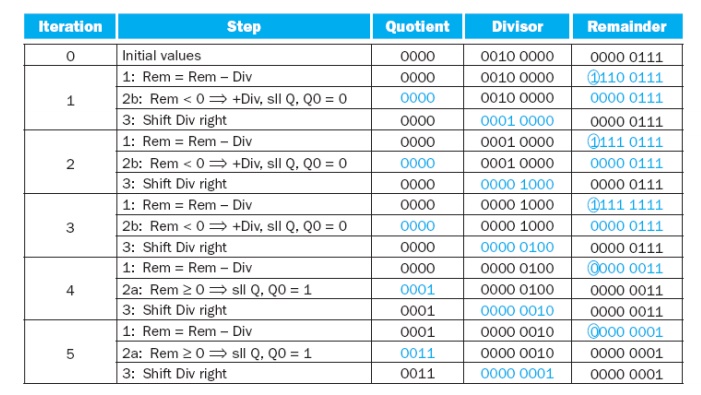
Fig. 2.10 Values of register in division algorithm

The above figure shows the value of each register for each of the steps, with the quotient being 3ten and the remainder 1ten. Notice that the test in step 2 of whether the remainder is positive or negative simply tests whether the sign bit of the Remainder register is a 0 or 1. The surprising requirement of this algorithm is that it takes n + 1 steps to get the proper quotient and remainder.

This algorithm and hardware can be refined to be faster and cheaper. The speedup comes from shifting the operands and the quotient simultaneously with the subtraction. This refinement halves the width of the adder and registers by noticing where there are unused portions of registers and adders.

SIGNED DIVISION

The one complication of signed division is that we must also set the sign of the remainder. Remember that the following equation must always hold:

Dividend = Quotient × Divisor + Remainder

To understand how to set the sign of the remainder, let’s look at the example of dividing all the combinations of ±7 ₁₀ by ±2 ₁₀.

The first case is easy:

+7 ÷ +2: Quotient = +3, Remainder = +1 Checking the results:

7 = 3 × 2 + (+1) = 6 + 1

If we change the sign of the dividend, the quotient must change as well:

–7 ÷ +2: Quotient = –3

Rewriting our basic formula to calculate the remainder:

Remainder = (Dividend – Quotient × Divisor) = –7 – (–3 × +2) = –7–(–6) = –1

So,

–7 ÷ +2: Quotient = –3, Remainder = –1

Checking the results again:

–7 = –3 × 2 + ( –1) = – 6 – 1

The following figure shows the revised hardware.

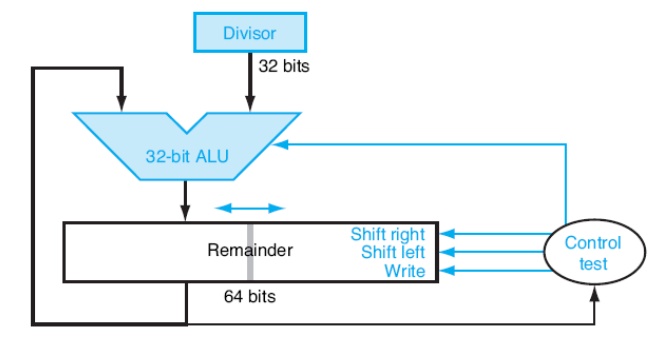
Fig. 2.11 Division hardware

The reason the answer isn’t a quotient of –4 and a remainder of +1, which would also fit this formula, is that the absolute value of the quotient would then change depending on the sign of the dividend and the divisor! Clearly, if

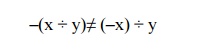
programming would be an even greater challenge. This anomalous behavior is avoided by following the rule that the dividend and remainder must have the same signs, no matter what the signs of the divisor and quotient. We calculate the other combinations by following the same rule:

Thus the correctly signed division algorithm negates the quotient if the signs of the operands are opposite and makes the sign of the nonzero remainder match the dividend.

Faster Division

Many adders can be used to speed up multiply, cannot be used to do the same trick for divide. The reason is that it is needed to know the sign of the difference before performing the next step of the algorithm, whereas with multiply we could calculate the 32 partial products immediately.

There are techniques to produce more than one bit of the quotient per step. The SRT division technique tries to guess several quotient bits per step, using a table lookup based on the upper bits of the dividend and remainder. It relies on subsequent steps to correct wrong guesses. A typical value today is 4 bits. The key is guessing the value to subtract. With binary division, there is only a single choice.

These algorithms use 6 bits from the remainder and 4 bits from the divisor to index a table that determines the guess for each step. The accuracy of this fast method depends on having proper values in the lookup table.

Restoring and non restoring division algorithm

•Assume ─ X register k-bit dividend

• Assume ─ Y the k-bit divisor

• Assume ─ S a sign-bit

1. Start: Load 0 into accumulator k-bit A and dividend X is loaded into the k-bit quotient register MQ.

2. Step A : Shift 2 k-bit register pair A -MQ left

3. Step B: Subtract the divisor Y from A.

4. Step C: If sign of A (msb) = 1, then reset MQ 0 (lsb) = 0 else set = 1.

5. Steps D: If MQ 0 = 0 add Y (restore the effect of earlier subtraction).

6. Steps A to D repeat again till the total number of cyclic operations = k. At the end, A has the remainder and MQ has the

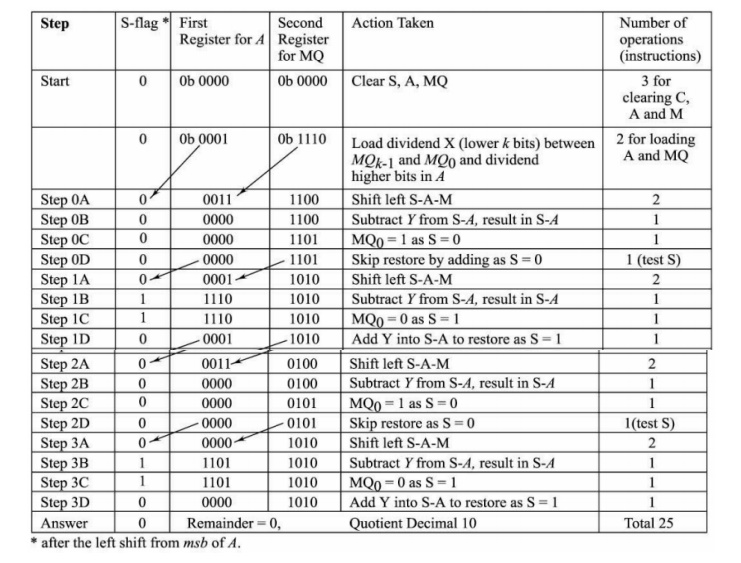
Fig. 2.12 Division of 4-bit number by 7-bit dividend

Division using Non-restoring Algorithm

•  Assume ─ that there is an accumulator and MQ register, each of k-bits • MQ 0, (lsb of MQ) bit gives the quotient, which is saved after a subtraction or addition

•  Total number of additions or subtractions are k-only and total number of shifts = k plus one addition for restoring remainder if needed

• Assume ─ that X register has (2 k−1) bit for dividend and Y has the k-bit divisor

• Assume ─ a sign-bit S shows the sign

1.     Load (upper half k −1 bits of the dividend X) into accumulator k-bit A and load dividend X (lower half bits into the lower k bits at quotient register MQ

• Reset sign S = 0

• Subtract the k bits divisor Y from S-A (1 plus k bits) and assign MQ 0 as per S

2.     If sign of A, S = 0, shift S plus 2 k-bit register pair A-MQ left and subtract the k bits divisor Y from S-A (1 plus k bits); else if sign of A, S = 1, shift S plus 2 k-bit register pair A - MQ left and add the divisor Y into S-A (1 plus k bits)

• Assign MQ 0 as per

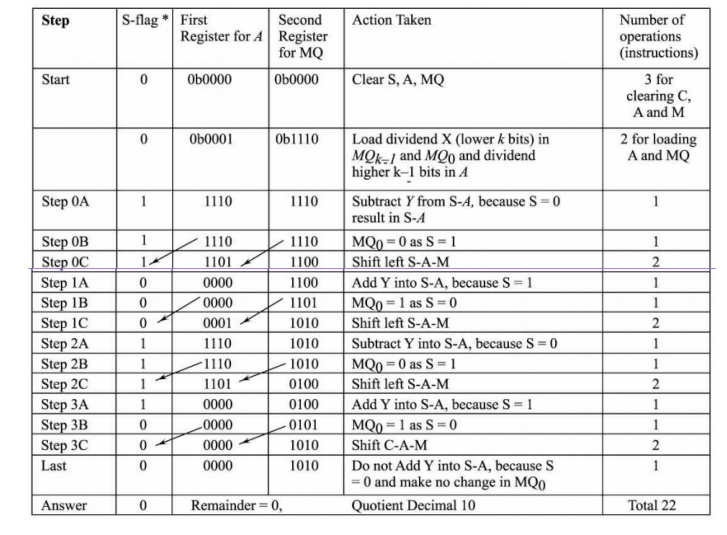
Fig. 2.13 Division using Non-restoring Algorithm

3.     Repeat step 2 again till the total number of operations = k.

4.     If at the last step, the sign of A in S = 1, then add Y into S -A to leave the correct remainder into A and also assign MQ 0 as per S, else do nothing.

5.       A has the remainder and MQ has the quotient