Chapter: Computer Architecture : Arithmetic Operations
Arithmetic Operations: Addition and Subtraction
ADDITION AND SUBTRACTION
Digits are added bit by bit from
right to left, with carries passed to the next digit to the left. Subtraction
uses addition: The appropriate operand is simply negated before being
added.overflow occurs when the result from an operation cannot be represented
with the available hardware. When adding operands with different signs, overflow
cannot occur. The reason is the sum must be no larger than one of the operands.
For example, –10 + 4 = –6. Since
the operands fit in 32 bits and the sum is no larger than an operand, the sum
must fit in 32 bits as well.
Therefore no overflow can occur
when adding positive and negative operands. There are similar
restrictions to the occurrence of overflow during subtract, but it’s just the
opposite
principle: When the signs of the
operands are the same, overflow cannot occur. Overflow occurs in subtraction
when a negative number is subtracted from a positive number and get a negative
result, or when a positive number is subtracted from a negative number and get
a positive result. This means a borrow occurred from the sign bit. Unsigned
integers are commonly used for memory addresses where overflows are ignored.
The computer designer must
therefore provide a way to ignore overflow in some cases and to recognize it in
others. The MIPS solution is to have two kinds of arithmetic instructions to
recognize the two choices:
■ Add
(add), add immediate (addi), and subtract (sub) cause exceptions on overflow.
■ Add
unsigned (addu), add immediate unsigned (addiu), and subtract unsigned (subu)
do not
cause exceptions on overflow.
Because C ignores overflows, the
MIPS C compilers will always generate the unsigned versions of the arithmetic
instructions addu, addiu, and subu no matter what the type of the
variables. The MIPS Fortran
compilers, however, pick the appropriate arithmetic instructions, depending on
the type of the operands.
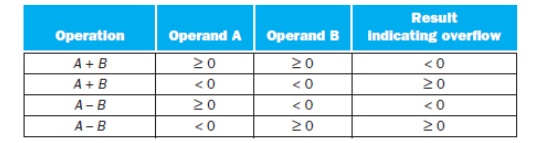
Fig. 2.1
Overflow conditions for addition and subtraction.
The computer designer must decide
how to handle arithmetic overflows. Although some languages like C ignore
integer overflow, languages like Ada and Fortran require that the program be
notified. The programmer or the programming environment must then decide what
to do when overflow occurs.
MIPS detects overflow with an
exception, also called an interrupt on many computers. An exception or
interrupt is essentially an unscheduled procedure call. The address of the
instruction that overflowed is saved in a register, and the computer jumps to a
predefined address to invoke the appropriate routine for that exception. The
interrupted address is saved so that in some situations the program can
continue after corrective code is executed. MIPS includes a register called the
exception program counter (EPC) to contain the address of the instruction that
caused the exception. The instruction move from system control (mfc0) is used
to copy EPC into a general-purpose register so that MIPS software has the
option of returning to the offending instruction via a jump register
instruction.
Addition and Subtraction Example
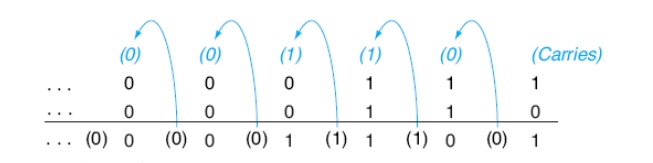
adding 6 to 7 in binary and then subtracting 6
from 7 in binary: 0000 0000 0000 0000 0000 0000 0000 0111two = 7
+
0000 0000 0000 0000 0000 0000 0000 0110two =
=
0000 0000 0000 0000 0000 0000 0000 1101two = 13
Subtracting 6 from
7 can be done directly:
0000 0000
0000 0000 0000 0000 0000 0111two = 7
– 0000 0000
0000 0000 0000 0000 0000 0110two = 6
=
0000 0000 0000 0000 0000 0000 0000 0001two = 1
or via addition using the two’s
complement representation of –6: 0000 0000
0000 0000 0000 0000 0000 0111two = 7
+ 1111 1111
1111 1111 1111 1111 1111 1010two = –6
=
0000 0000 0000 0000 0000 0000 0000 0001two = 1
Instructions available
Add, subtract, add immediate, add unsigned, subtract unsigned.
Carry-Look Ahead Adder
• Binary addition would
seem to be dramatically slower for large registers consider
0111 + 0011
carries
propagate left-to-right
So 64-bit
addition would be 8 times slower than 8- bit addition
•
It is possible to build a circuit called
a “carry look-ahead adder” that speeds up addition by
eliminating the need to “ripple” carries through the word.
• Carry
look-ahead
is expensive
• If
n is the number of bits in a ripple adder, the circuit complexity (number of
gates) is O(n)
• For
full carry look-ahead, the complexity is O(n3 )
• Complexity
can be reduced by rippling smaller look-aheads: e.g., each 16 bit group
is handled
by four 4-bit adders and the 16-bit adders are rippled into a
64-bit adder
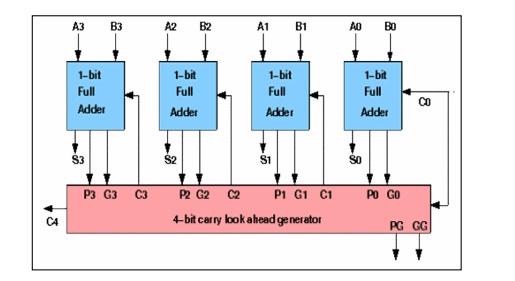
Fig. 2.2
Carry-look ahead adder
The advantage of the CLA scheme
used in this circuit is its simplicity, because each CLA block calculates the
generate and propagate signals for two bits only. This is much easier to
understand than the more complex variants presented in other textbooks, where
combinatorical logic is used to calculate the G and P signals of four or more
bits, and the resulting adder structure is slightly faster but also less
regular.
Related Topics