Applications of lists

APPLICATIONS OF LINKED LIST

1. Polynomial ADT

2. Radix Sort

3. Multilist

POLYNOMIAL MANIPULATION

Representation

Addition

Multiplication

Representation of a Polynomial: A polynomial is an expression that contains more than two terms. A term is made up of coefficient and exponent. An example of polynomial is

P(x) = 4x³+6x²+7x+9

A polynomial thus may be represented using arrays or linked lists. Array representation assumes that the exponents of the given expression are arranged from 0 to the highest value (degree), which is represented by the subscript of the array beginning with 0. The coefficients of the respective exponent are placed at an appropriate index in the array. The array representation for the above polynomial expression is given below:

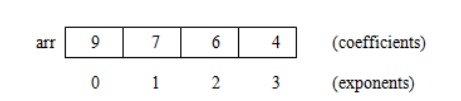
A polynomial may also be represented using a linked list. A structure may be defined such that it contains two parts- one is the coefficient and second is the corresponding exponent. The structure definition may be given as shown below:

struct polynomial

{

int coefficient; int exponent;

struct polynomial *next; };

Thus the above polynomial may be represented using linked list as shown below:

Addition of two Polynomials:

For adding two polynomials using arrays is straightforward method, since both the arrays may be added up element wise beginning from 0 to n-1, resulting in addition of two polynomials. Addition of two polynomials using linked list requires comparing the exponents, and wherever the exponents are found to be same, the coefficients are added up. For terms with different exponents, the complete term is simply added to the result thereby making it a part of addition result. The complete program to add two polynomials is given in subsequent section.

Multiplication of two Polynomials:

Multiplication of two polynomials however requires manipulation of each node such that the exponents are added up and the coefficients are multiplied. After each term of first polynomial is operated upon with each term of the second polynomial, then the result has to be added up by comparing the exponents and adding the coefficients for similar exponents and including terms as such with dissimilar exponents in the result. The ‘C’ program for polynom given below:

Program for Polynomial representation, addition and multiplication

/*Polynomial- Representation, Addition, Multiplication*/

Representation using structure

#include <stdio.h> #include <conio.h> #include <math.h>

typedef struct node { int power;

int coeff;

struct node *next;

}node;

node *  insert(node *head,int power1,float coeff1);

node *  create();

node * padd(node *p1,node *p2); void print(node *head);

node *insert(node *head,int power1,float coeff1)

{

node *p,*q;

p=(node*) malloc(sizeof(node)); p->power=power1; p->coeff=coeff1; p->next=NULL; if(head==NULL)

{

head=p; head->next=head; return(head);

}

if(power1>head->power)

{

p->next=head->next; head->next=p; head=p; return(head);

}

if(power1==head->power)

{

head->coeff=head->coeff+coeff1; return(head);

}

q=head;

while(q->next!=head && power1>=q->next->power) q=q->next;

if(p->power==q->power) q->coeff=q->coeff+coeff1;

else

{

p->next=q->next; q->next=p;

}

return(head);

}

node *create()

{

int n,i,power1; float coeff1;

node *head=NULL; printf("\nEnter No. of Terms:"); scanf("%d",&n);

printf("\nenter a term as a tuple of (power,coefficient) : "); for(i=1;i<=n;i++)

{ scanf("%d%f",&power1,&coeff1); head=insert(head,power1,coeff1);

}

return(head);

}

node * padd(node *p1,node *p2) { node *p;

node *head=NULL; int power;float coeff; p=p1->next;

do

{

head=insert(head,p->power,p->coeff); p=p->next;

} while(p!=p1->next); p=p2->next;

do

{

head=insert(head,p->power,p->coeff); p=p->next;

} while(p!=p2->next);

return(head);

}

void print( node *head) { node *p;

p=head->next; printf("\n"); do

{

printf("%6.2fx^%d ",p->coeff,p->power); p=p->next;

}while(p!=head->next);

}